Deep Clustering via Joint Convolutional Auto encoder Embedding and Relative Entropy Minimization

通过联合卷积自编码器嵌入和相对熵最小化实现深度聚类

Abstract

摘要

Image clustering is one of the most important computer vision applications, which has been extensively studied in literature. However, current clustering methods mostly suffer from lack of efficiency and s cal ability when dealing with large-scale and high-dimensional data. In this paper, we propose a new clustering model, called DEeP Embedded RegularIzed ClusTering (DEPICT), which efficiently maps data into a disc rim i native embedding subspace and precisely predicts cluster assignments. DEPICT generally consists of a multi no mi al logistic regression function stacked on top of a multi-layer convolutional auto encoder. We define a clustering objective function using relative entropy (KL divergence) minimization, regularized by a prior for the frequency of cluster assignments. An alternating strategy is then derived to optimize the objective by updating parameters and estimating cluster assignments. Furthermore, we employ the reconstruction loss functions in our auto encoder, as a data-dependent regular iz ation term, to prevent the deep embedding function from over fitting. In order to benefit from end-to-end optimization and eliminate the necessity for layer-wise pre training, we introduce a joint learning framework to minimize the unified clustering and reconstruction loss functions together and train all network layers simultaneously. Experimental results indicate the superiority and faster running time of DEPICT in realworld clustering tasks, where no labeled data is available for hyper-parameter tuning.

图像聚类是计算机视觉最重要的应用之一，已在文献中被广泛研究。然而，当前聚类方法在处理大规模高维数据时普遍存在效率和可扩展性不足的问题。本文提出了一种称为深度嵌入正则化聚类（DEPICT）的新模型，它能高效地将数据映射到判别性嵌入子空间并精确预测聚类分配。DEPICT通常由堆叠在多层卷积自编码器上的多项逻辑回归函数构成。我们通过相对熵（KL散度）最小化定义聚类目标函数，并以聚类分配频率的先验分布作为正则项，进而推导出交替优化策略来更新参数并估计聚类分配。此外，我们在自编码器中采用重构损失函数作为数据依赖的正则化项，以防止深度嵌入函数过拟合。为了获得端到端优化的优势并消除分层预训练的必要性，我们引入联合学习框架来同步最小化统一的聚类与重构损失函数，并同时训练所有网络层。实验结果表明，在现实世界无标签数据可供超参数调优的聚类任务中，DEPICT具有优越性能和更快的运行速度。

1. Introduction

1. 引言

Clustering is one of the fundamental research topics in machine learning and computer vision research, and it has gained significant attention for disc rim i native representation of data points without any need for supervisory sig- nals. The clustering problem has been extensively studied in various applications; however, the performance of standard clustering algorithms is adversely affected when dealing with high-dimensional data, and their time complexity dramatically increases when working with large-scale datasets. Tackling the curse of dimensionality, previous studies often initially project data into a low-dimensional manifold, and then cluster the embedded data in this new subspace [37, 45, 52]. Handling large-scale datasets, there are also several studies which select only a subset of data points to accelerate the clustering process [42, 22, 20].

聚类是机器学习和计算机视觉研究中的基础课题之一，因其能在无需监督信号的情况下实现数据点的判别性表征而备受关注。该问题已在众多应用场景中得到广泛研究，但传统聚类算法在处理高维数据时性能显著下降，面对大规模数据集时时间复杂度急剧攀升。为应对维度灾难，先前研究通常先将数据投影至低维流形，再在新子空间中对嵌入数据进行聚类[37,45,52]。针对大规模数据集，亦有研究通过选取数据点子集来加速聚类过程[42,22,20]。

Figure 1: Visualization to show the disc rim i native capability of embedding subspaces using MNIST-test data. (a) The space of raw data. (b) The embedding subspace of non-joint DEPICT using standard stacked denoising autoencoder (SdA). (c) The embedding subspace of joint $D E.$ - PICT using our joint learning approach (MdA).

图 1: 使用MNIST-test数据展示嵌入子空间原生能力的可视化。(a) 原始数据空间。(b) 非联合DEPICT使用标准堆叠去噪自编码器(SdA)的嵌入子空间。(c) 联合$D E.$ -PICT采用我们联合学习方法(MdA)的嵌入子空间。

However, dealing with real-world image data, existing clustering algorithms suffer from different issues: 1) Using inflexible hand-crafted features, which do not depend on the input data distribution; 2) Using shallow and linear embedding functions, which are not able to capture the non-linear nature of data; 3) Non-joint embedding and clustering processes, which do not result in an optimal embedding subspace for clustering; 4) Complicated clustering algorithms that require tuning the hyper-parameters using labeled data, which is not feasible in real-world clustering tasks.

然而，在处理现实世界的图像数据时，现有的聚类算法存在不同问题：1) 使用不灵活的手工特征，这些特征不依赖于输入数据分布；2) 使用浅层线性嵌入函数，无法捕捉数据的非线性特性；3) 嵌入和聚类过程非联合进行，无法得到最优的聚类嵌入子空间；4) 复杂的聚类算法需要使用带标签数据调整超参数，这在实际聚类任务中不可行。

To address the mentioned challenging issues, we propose a new clustering algorithm, called deep embedded regularized clustering (DEPICT), which exploits the advantages of both disc rim i native clustering methods and deep embedding models. DEPICT generally consists of two main parts, a multi no mi al logistic regression (soft-max) layer stacked on top of a multi-layer convolutional auto encoder. The softmax layer along with the encoder pathway can be considered as a disc rim i native clustering model, which is trained using the relative entropy $K L$ divergence) minimization. We further add a regular iz ation term based on a prior distribution for the frequency of cluster assignments. The regu lari z ation term penalizes unbalanced cluster assignments and prevents allocating clusters to outlier samples.

为了解决上述具有挑战性的问题，我们提出了一种新的聚类算法，称为深度嵌入正则化聚类 (DEPICT)，它结合了判别式聚类方法和深度嵌入模型的优势。DEPICT主要由两部分组成：一个多层卷积自编码器顶部堆叠的多项式逻辑回归 (soft-max) 层。softmax层与编码器路径可视为一个判别式聚类模型，该模型通过相对熵 (KL散度) 最小化进行训练。我们进一步基于聚类分配频率的先验分布添加了正则化项。该正则化项会惩罚不平衡的聚类分配，并防止将聚类分配给异常样本。

Although this deep clustering model is flexible enough to discriminate the complex real-world input data, it can easily get stuck in non-optimal local minima during training and result in undesirable cluster assignments. In order to avoid over fitting the deep clustering model to spurious data correlations, we utilize the reconstruction loss function of auto encoder models as a data-dependent regular iz ation term for training parameters.

尽管这种深度聚类模型足够灵活，能够区分复杂的现实世界输入数据，但在训练过程中很容易陷入非最优的局部极小值，导致不理想的聚类分配。为了避免深度聚类模型过度拟合虚假数据相关性，我们利用自编码器模型的重构损失函数作为数据依赖的正则化项来训练参数。

In order to benefit from a joint learning framework for embedding and clustering, we introduce a unified objective function including our clustering and auxiliary reconstruction loss functions. We then employ an alternating approach to efficiently update the parameters and estimate the cluster assignments. It is worth mentioning that in the standard learning approach for training a multi-layer autoencoder, the encoder and decoder parameters are first pretrained layer-wise using the reconstruction loss, and the encoder parameters are then fine-tuned using the objective function of the main task [48]. However, it has been argued that the non-joint fine-tuning step may overwrite the encoder parameters entirely and consequently cancel out the benefit of the layer-wise pre training step [68]. To avoid this problem and achieve optimal joint learning results, we simultan e ou sly train all of the encoder and decoder layers together along with the soft-max layer. To do so, we sum up the squared error reconstruction loss functions between the decoder and their corresponding (clean) encoder layers and add them to the clustering loss function.

为了从嵌入和聚类的联合学习框架中获益，我们引入了一个包含聚类和辅助重构损失函数的统一目标函数。随后采用交替优化方法高效更新参数并估计聚类分配。值得注意的是，在训练多层自动编码器 (autoencoder) 的标准学习方法中，通常先通过重构损失逐层预训练编码器和解码器参数，再使用主任务目标函数微调编码器参数 [48]。但有研究指出，这种非联合的微调步骤可能会完全覆盖编码器参数，从而抵消逐层预训练的优势 [68]。为避免该问题并获得最优联合学习效果，我们同步训练所有编码器层、解码器层及soft-max层。具体实现方式是将解码器与对应（干净）编码器层之间的平方误差重构损失函数求和，再叠加到聚类损失函数上。

Figure 1 demonstrates the importance of our joint learning strategy by comparing different data representations of MNIST-test data points [17] using principle component analysis (PCA) visualization. The first figure indicates the raw data representation; The second one shows the data points in the embedding subspace of non-joint DEPICT, in which the model is trained using the standard layer-wise stacked denoising auto encoder (SdA); The third one visualizes the data points in the embedding subspace of joint DEPICT, in which the model is trained using our multilayer denoising auto encoder learning approach (MdA). As shown, joint DEPICT using MdA learning approach provides a significantly more disc rim i native embedding subspace compared to non-joint DEPICT using standard SdA learning approach.

图 1: 通过主成分分析 (PCA) 可视化对比 MNIST 测试数据点 [17] 的不同数据表征，展示了我们联合学习策略的重要性。第一幅图展示原始数据表征；第二幅图显示非联合 DEPICT 嵌入子空间中的数据点，该模型采用标准逐层堆叠去噪自编码器 (SdA) 训练；第三幅图可视化联合 DEPICT 嵌入子空间中的数据点，该模型采用我们提出的多层去噪自编码器学习框架 (MdA) 训练。如图所示，采用 MdA 学习框架的联合 DEPICT 相比采用标准 SdA 学习框架的非联合 DEPICT，能提供显著更具判别性的嵌入子空间。

Moreover, experimental results show that DEPICT achieves superior or competitive results compared to the state-of-the-art algorithms on the image benchmark datasets while having faster running times. In addition, we compared different learning strategies for DEPICT, and confirm that our joint learning approach has the best results. It should also be noted that DEPICT does not require any hyper-parameter tuning using supervisory signals, and consequently is a better candidate for the real-world clustering tasks. Thus, we summarize the advantages of DEPICT as:

此外，实验结果表明，在图像基准数据集上，DEPICT 相比当前最优算法取得了更优或具有竞争力的结果，同时运行速度更快。我们还比较了 DEPICT 的不同学习策略，并证实我们的联合学习方法效果最佳。值得注意的是，DEPICT 无需使用监督信号进行任何超参数调优，因此更适合实际聚类任务。综上所述，DEPICT 的优势可归纳为：

• Providing a disc rim i native non-linear embedding subspace via the deep convolutional auto encoder; • Introducing an end-to-end joint learning approach, which unifies the clustering and embedding tasks, and avoids layer-wise pre training; • Achieving superior or competitive clustering results on high-dimensional and large-scale datasets with no need for hyper-parameter tuning using labeled data.

• 通过深度卷积自编码器提供判别式非线性嵌入子空间；
• 提出端到端联合学习方法，统一聚类和嵌入任务，避免逐层预训练；
• 在高维和大规模数据集上实现优异或具有竞争力的聚类结果，无需使用标注数据进行超参数调优。

2. Related Works

2. 相关工作

There is a large number of clustering algorithms in literature, which can be grouped into different perspectives, such as hierarchical [10, 54, 65], centroid-based [21, 4, 28, 2], graph-based [41, 29, 51, 26], sequential (temporal) [12, 40, 39, 69, 38], regression model based [8, 50], and subspace clustering models [1, 11, 7, 27]. In another sense, they are generally divided into two subcategories, generative and disc rim i native clustering algorithms. The generative algorithms like $K$ -means and Gaussian mixture model [5] explicitly represent the clusters using geometric properties of the feature space, and model the categories via the statistical distributions of input data. Unlike the generative clustering algorithms, the disc rim i native methods directly identify the categories using their separating hyper planes regardless of data distribution. Information theoretic [19, 3, 15], maxmargin [67, 58], and spectral graph [25] algorithms are examples of disc rim i native clustering models. Generally it has been argued that the disc rim i native models often have better results compared to their generative counterparts, since they have fewer assumptions about the data distribution and directly separate the clusters, but their training can suffer from over fitting or getting stuck in undesirable local minima [15, 25, 33]. Our DEPICT algorithm is also a discriminative clustering model, but it benefits from the auxiliary reconstruction task of auto encoder to alleviate this issues in training of our disc rim i native clustering algorithm.

文献中存在大量聚类算法，可从不同角度进行分类，例如层次聚类 [10, 54, 65]、基于中心点 [21, 4, 28, 2]、基于图 [41, 29, 51, 26]、时序 [12, 40, 39, 69, 38]、基于回归模型 [8, 50] 以及子空间聚类模型 [1, 11, 7, 27]。另一种分类方式将其划分为生成式与判别式聚类算法。生成式算法如 $K$ 均值和高斯混合模型 [5] 通过特征空间的几何特性显式表示聚类，并基于输入数据的统计分布建模类别。与生成式不同，判别式方法直接利用分隔超平面识别类别而不考虑数据分布，例如信息论 [19, 3, 15]、最大间隔 [67, 58] 和谱图 [25] 算法。一般认为判别式模型由于对数据分布假设更少且直接分离聚类，效果优于生成式，但其训练可能面临过拟合或陷入不良局部极小值 [15, 25, 33]。我们的DEPICT算法也属于判别式聚类模型，但通过自编码器的辅助重构任务缓解了判别式聚类算法训练中的这些问题。

There are also several studies regarding the combination of clustering with feature embedding learning. Ye et al. introduced a kernelized $K$ -means algorithm, denoted by DisKmeans, where embedding to a lower dimensional subspace via linear discriminant analysis $(L D A)$ is jointly learned with $K$ -means cluster assignments [62]. [49] proposed to a new method to simultaneously conduct both clustering and feature embedding/selection tasks to achieve better performance. But these models suffer from having shallow and linear embedding functions, which cannot represent the non-linearity of real-world data.

关于聚类与特征嵌入学习结合的研究也有多项进展。Ye等人提出了一种核化K均值算法(DisKmeans)，通过线性判别分析(LDA)将数据嵌入到低维子空间，并与K均值聚类分配联合学习[62]。[49]提出了一种新方法，能同时执行聚类和特征嵌入/选择任务以获得更优性能。但这些模型存在嵌入函数浅层且线性的缺陷，无法表征现实数据的非线性特征。

A joint learning framework for updating code books and estimating image clusters was proposed in [57] while SIFT features are used as input data. A deep structure, named TAGnet was introduced in [52], where two layers of sparse coding followed by a clustering algorithm are trained with an alternating learning approach. Similar work is presented in [53] that formulates a joint optimization framework for disc rim i native clustering and feature extraction using sparse coding. However, the inference complexity of sparse coding forces the model in [53] to reduce the dimension of input data with $P C A$ and the model in [52] to use an approximate solution. Hand-crafted features and dimension reduction techniques degrade the clustering performance by neglecting the distribution of input data.

[57]提出了一种联合学习框架，用于更新码本和估计图像聚类，同时使用SIFT特征作为输入数据。[52]引入了一种名为TAGnet的深度结构，其中两层稀疏编码后接聚类算法，采用交替学习方法进行训练。[53]提出了类似工作，构建了一个联合优化框架，通过稀疏编码实现判别式聚类和特征提取。然而，稀疏编码的推理复杂性迫使[53]中的模型使用PCA降低输入数据维度，[52]中的模型则采用近似解。手工特征和降维技术会因忽略输入数据分布而降低聚类性能。

Tian et al. learned a non-linear embedding of the affinity graph using a stacked auto encoder, and then obtained the clusters in the embedding subspace via $K$ -means [45]. Trigeorgis et al. extended semi non-negative matrix factorization (semi-NMF) to stacked multi-layer (deep) semi-NMF to capture the abstract information in the top layer. Afterwards, they run $K$ -means over the embedding subspace for cluster assignments [46]. More recently, Xie et al. employed denoising stacked auto encoder learning approach, and first pretrained the model layer-wise and then fine-tuned the encoder pathway stacked by a clustering algorithm using Kullback-Leibler divergence minimization [56]. Unlike these models that require layer-wise pre training as well as non-joint embedding and clustering learning, DEPICT utilizes an end-to-end optimization for training all network layers simultaneously using the unified clustering and reconstruction loss functions.

Tian等人利用堆叠自编码器学习亲和图的非线性嵌入，然后通过$K$-means在嵌入子空间中获得聚类[45]。Trigeorgis等人将半非负矩阵分解(semi-NMF)扩展到堆叠多层(深度)semi-NMF，以捕获顶层的抽象信息。随后，他们在嵌入子空间上运行$K$-means进行聚类分配[46]。最近，Xie等人采用去噪堆叠自编码器学习方法，首先逐层预训练模型，然后使用Kullback-Leibler散度最小化通过聚类算法微调编码器路径[56]。与这些需要逐层预训练以及非联合嵌入和聚类学习的模型不同，DEPICT采用端到端优化，使用统一的聚类和重构损失函数同时训练所有网络层。

Yang et al. introduced a new clustering model, named JULE, based on a recurrent framework, where data is represented via a convolutional neural network and embedded data is iterative ly clustered using an agglom erat ive clustering algorithm [60]. They derived a unified loss function consisting of the merging process for agglom erat ive clustering and updating the parameters of the deep representation. While JULE achieved good results using the joint learning approach, it requires tuning of a large number of hyperparameters, which is not practical in real-world clustering tasks. In contrast, our model does not need any supervisory signals for hyper-parameter tuning.

Yang等人提出了一种基于循环框架的新型聚类模型JULE，该模型通过卷积神经网络表示数据，并采用凝聚式聚类算法对嵌入数据进行迭代聚类[60]。他们推导出一个统一的损失函数，包含凝聚式聚类的合并过程和深度表征参数的更新。虽然JULE通过联合学习方法取得了良好效果，但需要调整大量超参数，这在实际聚类任务中并不实用。相比之下，我们的模型不需要任何监督信号来进行超参数调优。

3. Deep Embedded Regularized Clustering

3. 深度嵌入式正则化聚类

In this section, we first introduce the clustering objective function and the corresponding optimization algorithm, which alternates between estimating the cluster assignments and updating model parameters. Afterwards, we show the architecture of DEPICT and provide the joint learning framework to simultaneously train all network layers using the unified clustering and reconstruction loss functions.

在本节中，我们首先介绍聚类目标函数及对应的优化算法，该算法交替执行聚类分配估计和模型参数更新。随后展示DEPICT的架构，并提供联合学习框架，通过统一的聚类和重构损失函数同时训练所有网络层。

3.1. DEPICT Algorithm

3.1. DEPICT算法

Let’s consider the clustering task of $N$ samples, $\mathbf{X}=$ $\left[\mathbf{x}{1},...,\mathbf{x}{n}\right]$ , into $K$ categories, where each sample $\mathbf{x}{i}\in\mathbf{\Gamma}$ $\mathbb{R}^{d_{x}}$ . Using the embedding function, $\varphi_{W}:X\to Z$ , we are able to map raw samples into the embedding subspace $\mathbf{Z}=[\mathbf{z}{1},...,\mathbf{z}{n}]$ , where each $\mathbf{z}{i}\in\mathbb{R}^{d_{z}}$ has a much lower dimension compared to the input data (i.e. $d_{z}\ll d_{x}$ ). Given the embedded features, we use a multi no mi al logistic regression (soft-max) function $f_{\theta}:Z\to Y$ to predict the probabilistic cluster assignments as follows.

考虑将 $N$ 个样本 $\mathbf{X}=$ $\left[\mathbf{x}{1},...,\mathbf{x}{n}\right]$ 聚类为 $K$ 个类别的任务，其中每个样本 $\mathbf{x}{i}\in\mathbf{\Gamma}$ $\mathbb{R}^{d_{x}}$。通过嵌入函数 $\varphi_{W}:X\to Z$，我们可以将原始样本映射到嵌入子空间 $\mathbf{Z}=[\mathbf{z}{1},...,\mathbf{z}{n}]$，其中每个 $\mathbf{z}{i}\in\mathbb{R}^{d_{z}}$ 的维度远低于输入数据（即 $d_{z}\ll d_{x}$）。给定嵌入特征后，我们使用多项逻辑回归（soft-max）函数 $f_{\theta}:Z\to Y$ 来预测概率聚类分配，如下所示。

$$
p_{i k}=P(y_{i}=k|\mathbf{z}_{i},\boldsymbol{\Theta})=\frac{e x p(\boldsymbol{\theta}_{k}^{T}\mathbf{z}_{i})}{\displaystyle\sum_{k^{\prime}=1}^{K}e x p(\boldsymbol{\theta}_{k^{\prime}}^{T}\mathbf{z}_{i})},
$$

$$
p_{i k}=P(y_{i}=k|\mathbf{z}_{i},\boldsymbol{\Theta})=\frac{e x p(\boldsymbol{\theta}_{k}^{T}\mathbf{z}_{i})}{\displaystyle\sum_{k^{\prime}=1}^{K}e x p(\boldsymbol{\theta}_{k^{\prime}}^{T}\mathbf{z}_{i})},
$$

where $\pmb{\Theta}=[\pmb{\theta}{1},...,\pmb{\theta}{k}]\in\mathbb{R}^{d_{z}\times K}$ are the soft-max function parameters, and $p_{i k}$ indicates the probability of the $i$ -th sample belonging to the $k$ -th cluster.

其中 $\pmb{\Theta}=[\pmb{\theta}{1},...,\pmb{\theta}{k}]\in\mathbb{R}^{d_{z}\times K}$ 是 soft-max 函数的参数，$p_{i k}$ 表示第 $i$ 个样本属于第 $k$ 个簇的概率。

In order to define our clustering objective function, we employ an auxiliary target variable $\mathbf{Q}$ to refine the model predictions iterative ly. To do so, we first use KullbackLeibler $(K L)$ divergence to decrease the distance between the model prediction $\mathbf{P}$ and the target variable $\mathbf{Q}$ .

为了定义我们的聚类目标函数，我们采用辅助目标变量 $\mathbf{Q}$ 来迭代优化模型预测。具体而言，首先使用KullbackLeibler $(KL)$ 散度来缩小模型预测 $\mathbf{P}$ 与目标变量 $\mathbf{Q}$ 之间的距离。

$$
\mathcal{L}=K L(\mathbf{Q}||\mathbf{P})=\frac{1}{N}\sum_{i=1}^{N}\sum_{k=1}^{K}q_{i k}\log\frac{q_{i k}}{p_{i k}},
$$

$$
\mathcal{L}=K L(\mathbf{Q}||\mathbf{P})=\frac{1}{N}\sum_{i=1}^{N}\sum_{k=1}^{K}q_{i k}\log\frac{q_{i k}}{p_{i k}},
$$

In order to avoid degenerate solutions, which allocate most of the samples to a few clusters or assign a cluster to outlier samples, we aim to impose a regular iz ation term to the target variable. To this end, we first define the empirical label distribution of target variables as:

为了避免退化解（即大部分样本被分配到少数几个簇或为离群样本单独分配簇的情况），我们旨在对目标变量施加一个正则化项。为此，我们首先将目标变量的经验标签分布定义为：

$$
f_{k}=P(\mathbf{y}=k)=\frac{1}{N}\sum_{i}q_{i k},
$$

$$
f_{k}=P(\mathbf{y}=k)=\frac{1}{N}\sum_{i}q_{i k},
$$

where $f_{k}$ can be considered as the soft frequency of cluster assignments in the target distribution. Using this empirical distribution, we are able to enforce our preference for having balanced assignments by adding the following $K L$ divergence to the loss function.

其中 $f_{k}$ 可视为目标分布中聚类分配的软频率。通过使用这一经验分布，我们能够通过向损失函数添加以下 $K L$ 散度来强制实现平衡分配的偏好。

$$
\begin{array}{l}{{\displaystyle\mathcal{L}=K L({\bf Q}||{\bf P})+K L({\bf f}||{\bf u})}}\ {{\displaystyle~=\left[\frac{1}{N}\sum_{i=1}^{N}\sum_{k=1}^{K}q_{i k}\log\frac{q_{i k}}{p_{i k}}\right]+\left[\frac{1}{N}\sum_{k=1}^{K}f_{k}\log\frac{f_{k}}{u_{k}}\right]}}\ {{\displaystyle~=\frac{1}{N}\sum_{i=1}^{N}\sum_{k=1}^{K}q_{i k}\log\frac{q_{i k}}{p_{i k}}+q_{i k}\log\frac{f_{k}}{u_{k}}},}\end{array}
$$

$$
\begin{array}{l}{{\displaystyle\mathcal{L}=K L({\bf Q}||{\bf P})+K L({\bf f}||{\bf u})}}\ {{\displaystyle~=\left[\frac{1}{N}\sum_{i=1}^{N}\sum_{k=1}^{K}q_{i k}\log\frac{q_{i k}}{p_{i k}}\right]+\left[\frac{1}{N}\sum_{k=1}^{K}f_{k}\log\frac{f_{k}}{u_{k}}\right]}}\ {{\displaystyle~=\frac{1}{N}\sum_{i=1}^{N}\sum_{k=1}^{K}q_{i k}\log\frac{q_{i k}}{p_{i k}}+q_{i k}\log\frac{f_{k}}{u_{k}}},}\end{array}
$$

where $\mathbf{u}$ is the uniform prior for the empirical label distribution. While the first term in the objective minimizes the distance between the target and model prediction distributions, the second term balances the frequency of clusters in the target variables. Utilizing the balanced target variables, we can force the model to have more balanced predictions (cluster assignments) $\mathbf{P}$ indirectly. It is also simple to change the prior from the uniform distribution to any arbitrary distribution in the objective function if there is any extra knowledge about the frequency of clusters.

其中 $\mathbf{u}$ 是经验标签分布的均匀先验。目标函数的第一项最小化目标分布与模型预测分布之间的距离，第二项则平衡目标变量中聚类的频率。通过使用平衡后的目标变量，我们可以间接迫使模型产生更平衡的预测（聚类分配） $\mathbf{P}$。若存在关于聚类频率的额外先验知识，只需在目标函数中将均匀分布先验替换为任意分布即可。

An alternating learning approach is utilized to optimize the objective function. Using this approach, we estimate the target variables $\mathbf{Q}$ via fixed parameters (expectation step), and update the parameters while the target variables $\mathbf{Q}$ are assumed to be known (maximization step). The problem to infer the target variable $\mathbf{Q}$ has the following objective:

采用交替学习的方法来优化目标函数。通过这种方法，我们利用固定参数估计目标变量 $\mathbf{Q}$ (期望步骤)，并在假设目标变量 $\mathbf{Q}$ 已知的情况下更新参数(最大化步骤)。推断目标变量 $\mathbf{Q}$ 的问题具有以下目标：

$$
\operatorname*{min}{\mathbf{Q}}\frac{1}{N}\sum_{i=1}^{N}\sum_{k=1}^{K}q_{i k}\log\frac{q_{i k}}{p_{i k}}+q_{i k}\log\frac{f_{k}}{u_{k}},
$$

$$
\operatorname*{min}{\mathbf{Q}}\frac{1}{N}\sum_{i=1}^{N}\sum_{k=1}^{K}q_{i k}\log\frac{q_{i k}}{p_{i k}}+q_{i k}\log\frac{f_{k}}{u_{k}},
$$

where the target variables are constrained to $\textstyle\sum_{k}q_{i k}=1$ . This problem can be solved using first order methods, such as gradient descent, projected gradient descent, and Nesterov optimal method [24], which only require the objective function value and its (sub)gradient at each iteration. In the following equation, we show the partial derivative of the objective function with respect to the target variables.

其中目标变量受限于 $\textstyle\sum_{k}q_{i k}=1$。该问题可采用一阶优化方法求解，例如梯度下降法、投影梯度下降法和Nesterov最优方法 [24]，这些方法只需每次迭代时获取目标函数值及其(次)梯度。下方公式展示了目标函数对目标变量的偏导数。

$$
\frac{\partial\mathcal{L}}{\partial q_{i k}}\propto\log\left(\frac{q_{i k}f_{k}}{p_{i k}}\right)+\frac{q_{i k}}{\displaystyle\sum_{i^{\prime}=1}^{N}q_{i^{\prime}k}}+1,
$$

$$
\frac{\partial\mathcal{L}}{\partial q_{i k}}\propto\log\left(\frac{q_{i k}f_{k}}{p_{i k}}\right)+\frac{q_{i k}}{\displaystyle\sum_{i^{\prime}=1}^{N}q_{i^{\prime}k}}+1,
$$

Investigating this problem more carefully, we approximate the gradient in Eq.(6) by removing the second term, since the number of samples $\mathbf{N}$ is often big enough to ignore the second term. Setting the gradient equal to zero, we are now able to compute the closed form solution for $\mathbf{Q}$ accordingly.

为了更仔细地研究这个问题，我们通过移除第二项来近似方程(6)中的梯度，因为样本数$\mathbf{N}$通常足够大，可以忽略第二项。将梯度设为零，我们现在能够相应地计算出$\mathbf{Q}$的闭式解。

$$
q_{i k}=\frac{p_{i k}/(\sum_{i^{\prime}}p_{i^{\prime}k})^{\frac{1}{2}}}{\sum_{k^{\prime}}p_{i k^{\prime}}/(\sum_{i^{\prime}}p_{i^{\prime}k^{\prime}})^{\frac{1}{2}}},
$$

$$
q_{i k}=\frac{p_{i k}/(\sum_{i^{\prime}}p_{i^{\prime}k})^{\frac{1}{2}}}{\sum_{k^{\prime}}p_{i k^{\prime}}/(\sum_{i^{\prime}}p_{i^{\prime}k^{\prime}})^{\frac{1}{2}}},
$$

For the maximization step, we update the network parameters $\pmb{\psi}={\Theta,\mathbf{W}}$ using the estimated target variables with

对于最大化步骤，我们使用估计的目标变量更新网络参数 $\pmb{\psi}={\Theta,\mathbf{W}}$

the following objective function.

以下目标函数。

$$
\operatorname*{min}{\psi}-\frac{1}{N}\sum_{i=1}^{N}\sum_{k=1}^{K}q_{i k}\log p_{i k},
$$

$$
\operatorname*{min}{\psi}-\frac{1}{N}\sum_{i=1}^{N}\sum_{k=1}^{K}q_{i k}\log p_{i k},
$$

Interestingly, this problem can be considered as a standard cross entropy loss function for classification tasks, and the parameters of soft-max layer $\Theta$ and embedding function $\mathbf{W}$ can be efficiently updated by back propagating the error.

有趣的是，这个问题可以被视为分类任务的标准交叉熵损失函数，而 soft-max 层的参数 $\Theta$ 和嵌入函数 $\mathbf{W}$ 可以通过误差反向传播高效更新。

3.2. DEPICT Architecture

3.2. DEPICT架构

In this section, we extend our general clustering loss function using a denoising auto encoder. The deep embedding function is useful for capturing the non-linear nature of input data; However, it may overfit to spurious data correlations and get stuck in undesirable local minima during training. To avoid this over fitting, we employ autoencoder structures and use the reconstruction loss function as a data-dependent regular iz ation for training the parameters. Therefore, we design DEPICT to consist of a soft-max layer stacked on top of a multi-layer convolutional auto encoder. Due to the promising performance of strided convolutional layers in [32, 63], we employ convolutional layers in our encoder and strided convolutional layers in the decoder pathways, and avoid deterministic spatial pooling layers (like max-pooling). Strided convolutional layers allow the network to learn its own spatial upsampling, providing a better generation capability.

在本节中，我们使用去噪自编码器扩展了通用聚类损失函数。深度嵌入函数能有效捕捉输入数据的非线性特征，但可能过度拟合虚假数据相关性并在训练中陷入不良局部极小值。为避免过拟合，我们采用自编码器结构，并将重构损失函数作为数据依赖的正则项来训练参数。因此，我们将DEPICT设计为由多层卷积自编码器顶部堆叠soft-max层构成。基于[32, 63]中步进卷积层的优异表现，我们在编码器中使用常规卷积层，在解码器路径采用步进卷积层，同时避免确定性空间池化层（如最大池化）。步进卷积层使网络能够自主学习空间上采样，从而获得更好的生成能力。

Unlike the standard learning approach for denoising autoencoders, which contains layer-wise pre training and then fine-tuning, we simultaneously learn all of the auto encoder and soft-max layers. As shown in Figure 2, DEPICT consists of the following components:

与去噪自编码器的标准学习方法（包含分层预训练和微调）不同，我们同时学习所有自编码器和soft-max层。如图2所示，DEPICT包含以下组件：

1. Corrupted feed forward (encoder) pathway maps the noisy input data into the embedding subspace using a few convolutional layers followed by a fully connected layer. The following equation indicates the output of each layer in the noisy encoder pathway.
2. 损坏的前馈（编码器）路径通过几个卷积层和一个全连接层将含噪输入数据映射到嵌入子空间。以下公式表示含噪编码器路径中每一层的输出。

$$
\tilde{\mathbf{z}}^{l}=D r o p o u t\left[g(\mathbf{W}_{e}^{l}\tilde{\mathbf{z}}^{l-1})\right],
$$

$$
\tilde{\mathbf{z}}^{l}=D r o p o u t\left[g(\mathbf{W}_{e}^{l}\tilde{\mathbf{z}}^{l-1})\right],
$$

where $\tilde{\mathbf{z}}^{l}$ are the noisy features of the $l$ -th layer, Dropout is a stochastic mask function that randomly sets a subset of its inputs to zero [44], $g$ is the activation function of convolutional or fully connected layers, and $\mathbf{W}_{e}^{l}$ indicates the weights of the $l$ -th layer in the encoder. Note that the first layer features, $\tilde{\mathbf{z}}^{0}$ , are equal to the noisy input data, $\tilde{\bf x}$ .

其中 $\tilde{\mathbf{z}}^{l}$ 是第 $l$ 层的噪声特征，Dropout 是一种随机掩码函数，会随机将其输入的子集置零 [44]，$g$ 是卷积层或全连接层的激活函数，$\mathbf{W}_{e}^{l}$ 表示编码器中第 $l$ 层的权重。注意第一层特征 $\tilde{\mathbf{z}}^{0}$ 等于含噪输入数据 $\tilde{\bf x}$。

2. Followed by the corrupted encoder, the decoder pathway reconstructs the input data through a fully connected and multiple strided convolutional layers as follows,
3. 接着，损坏的编码器之后，解码器路径通过全连接层和多个跨步卷积层按以下方式重建输入数据，

$$
\hat{\mathbf{z}}^{l-1}=g(\mathbf{W}_{d}^{l}\hat{\mathbf{z}}^{l}),
$$

$$
\hat{\mathbf{z}}^{l-1}=g(\mathbf{W}_{d}^{l}\hat{\mathbf{z}}^{l}),
$$

where $\hat{\mathbf{z}}^{l}$ is the $l$ -th reconstruction layer output, and $\mathbf{W}_{d}^{l}$ shows the weights for the $l$ -th layer of the decoder. Note that input reconstruction, $\hat{\bf x}$ , is equal to $\hat{\mathbf{z}}^{0}$ .

其中 $\hat{\mathbf{z}}^{l}$ 是第 $l$ 个重构层的输出，$\mathbf{W}_{d}^{l}$ 表示解码器第 $l$ 层的权重。注意输入重构 $\hat{\bf x}$ 等于 $\hat{\mathbf{z}}^{0}$。

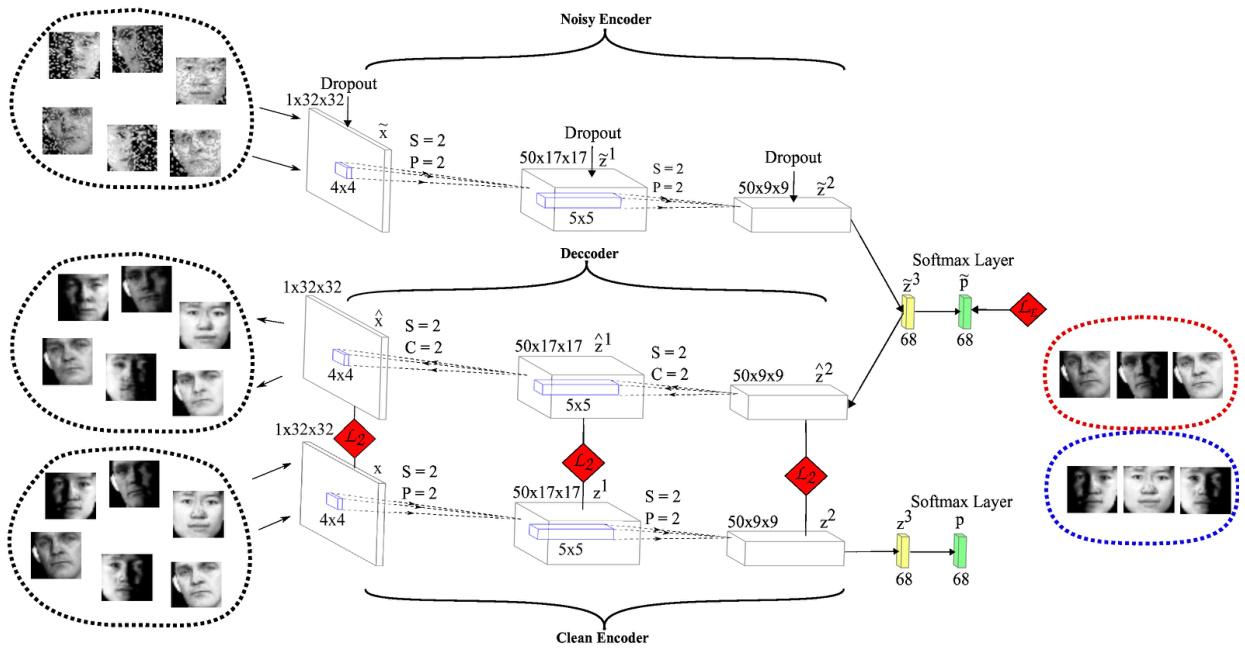
Figure 2: Architecture of DEPICT for CMU-PIE dataset. DEPICT consists of a soft-max layer stacked on top of a multilayer convolutional auto encoder. In order to illustrate the joint learning framework, we consider the following four pathways for DEPICT: Noisy (corrupted) encoder, Decoder, Clean encoder and Soft-max layer. The clustering loss function, $L_{E}$ , is applied on the noisy pathway, and the reconstruction loss functions, $L_{2}$ , are between the decoder and clean encoder layers. The output size of convolutional layers, kernel sizes, strides (S), paddings (P) and crops (C) are also shown.

图 2: CMU-PIE数据集上DEPICT的架构。DEPICT由堆叠在多层卷积自编码器顶部的soft-max层组成。为了说明联合学习框架，我们为DEPICT考虑了以下四条路径：含噪(损坏)编码器、解码器、干净编码器和Soft-max层。聚类损失函数$L_{E}$应用于含噪路径，重建损失函数$L_{2}$位于解码器与干净编码器层之间。图中同时标明了卷积层的输出尺寸、卷积核大小、步长(S)、填充(P)和裁剪(C)参数。

3. Clean feed forward (encoder) pathway shares its weights with the corrupted encoder, and infers the clean embedded features. The following equation shows the outputs of the clean encoder, which are used in the reconstruction loss functions and obtaining the final cluster assignments.
4. 干净前馈（编码器）路径与受损编码器共享权重，并推断干净的嵌入特征。以下方程展示了干净编码器的输出，这些输出用于重构损失函数和获取最终的聚类分配。

$$
\begin{array}{r}{\mathbf{z}^{l}=g(\mathbf{W}_{e}^{l}\mathbf{z}^{l-1}),}\end{array}
$$

$$
\begin{array}{r}{\mathbf{z}^{l}=g(\mathbf{W}_{e}^{l}\mathbf{z}^{l-1}),}\end{array}
$$

where $\mathbf{z}^{l}$ is the clean output of the $l$ -th layer in the encoder. Consider the first layer features $\mathbf{z}^{0}$ equal to input data $\mathbf{x}$ . 4) Given the top layer of the corrupted and clean encoder pathways as the embedding subspace, the soft-max layer obtains the cluster assignments using Eq.(1).

其中$\mathbf{z}^{l}$是编码器第$l$层的纯净输出。设第一层特征$\mathbf{z}^{0}$等于输入数据$\mathbf{x}$。4) 将含噪路径和纯净路径编码器的顶层作为嵌入子空间，通过式(1)的soft-max层获得聚类分配结果。

Note that we compute target variables $\mathbf{Q}$ using the clean pathway, and model prediction P via the corrupted pathway. Hence, the clustering loss function $K L(\mathbf{Q}||\tilde{\mathbf{P}})$ forces the model to have invariant features with respect to noise. In other words, the model is assumed to have a dual role: a clean model, which is used to compute the more accurate target variables; and a noisy model, which is trained to achieve noise-invariant predictions.

注意，我们通过干净路径计算目标变量 $\mathbf{Q}$，而通过污染路径计算模型预测 P。因此，聚类损失函数 $K L(\mathbf{Q}||\tilde{\mathbf{P}})$ 迫使模型具备对噪声不变的特征。换句话说，该模型被赋予双重角色：一个用于计算更准确目标变量的干净模型，以及一个训练用于实现噪声不变预测的污染模型。

As a crucial point, DEPICT algorithm provides a joint learning framework that optimizes the soft-max and autoencoder parameters together.

关键点在于，DEPICT算法提供了一个联合学习框架，能够同时优化soft-max和自动编码器参数。

$$
\operatorname*{min}{\psi}-\frac{1}{N}\sum_{i=1}^{N}\sum_{k=1}^{K}q_{i k}\log\tilde{p}{i k}+\frac{1}{N}\sum_{i=1}^{N}\sum_{l=0}^{L-1}\frac{1}{|\mathbf{z}{i}^{l}|}|\mathbf{z}{i}^{l}-\hat{\mathbf{z}}{i}^{l}|_{2}^{2},
$$

$$
\operatorname*{min}{\psi}-\frac{1}{N}\sum_{i=1}^{N}\sum_{k=1}^{K}q_{i k}\log\tilde{p}{i k}+\frac{1}{N}\sum_{i=1}^{N}\sum_{l=0}^{L-1}\frac{1}{|\mathbf{z}{i}^{l}|}|\mathbf{z}{i}^{l}-\hat{\mathbf{z}}{i}^{l}|_{2}^{2},
$$

Algorithm 1: DEPICT Algorithm

算法 1: DEPICT 算法

使用聚类算法初始化 Q
2 while 未收敛 do 2 i logpikl
min 3 4 ik
(t) α ecp(0tz) 4 Pik
(t) α Pik / (i Pi'k) 2
qik 6 end

where $|\mathbf{z}_{i}^{l}|$ is the output size of the $l$ -th hidden layer (input for $l=0$ ), and $L$ is the depth of the auto encoder model.

其中 $|\mathbf{z}_{i}^{l}|$ 是第 $l$ 个隐藏层的输出尺寸(当 $l=0$ 时为输入尺寸)，$L$ 是自编码器模型的深度。

The benefit of joint learning frameworks for training multi-layer auto encoders is also reported in semisupervised classification tasks [34, 68]. However, DEPICT is different from previous studies, since it is designed for the unsupervised clustering task, it also does not require maxpooling switches used in stacked what-where auto encoder (SWWAE) [68], and lateral (skip) connections between encoder and decoder layers used in ladder network [34]. Algorithm 1 shows a brief description of DEPICT algorithm.

联合学习框架在训练多层自动编码器方面的优势也在半监督分类任务中得到了报道 [34, 68]。然而，DEPICT 与之前的研究不同，因为它是为无监督聚类任务设计的，也不需要堆叠式 what-where 自动编码器 (SWWAE) [68] 中使用的最大池化开关，以及阶梯网络 [34] 中使用的编码器和解码器层之间的横向（跳跃）连接。算法 1 简要描述了 DEPICT 算法。

4. Experiments

4. 实验

In this section, we first evaluate $D E P I C T^{1}$ in comparison with state-of-the-art clustering methods on several benchmark image datasets. Then, the running speed of the best clustering models are compared. Moreover, we examine different learning approaches for training DEPICT. Finally, we analyze the performance of DEPICT model on semisupervised classification tasks.

在本节中，我们首先在多个基准图像数据集上将 $DEPICT^{1}$ 与最先进的聚类方法进行比较评估。随后，对比了最佳聚类模型的运行速度。此外，我们研究了训练 DEPICT 的不同学习方法。最后，分析了 DEPICT 模型在半监督分类任务上的性能表现。

Datasets: In order to show that DEPICT works well with various kinds of datasets, we have chosen the following handwritten digit and face image datasets. Considering that clustering tasks are fully unsupervised, we concatenate the training and testing samples when applicable. MNIST-full: A dataset containing a total of 70,000 handwritten digits with 60,000 training and 10,000 testing samples, each being a 32 by 32 monochrome image [17]. MNIST-test: A dataset which only consists of the testing part of MNIST-full data. USPS: It is a handwritten digits dataset from the USPS postal service, containing 11,000 samples of 16 by 16 images. CMU-PIE: A dataset including 32 by 32 face images of 68 people with 4 different expressions [43]. YoutubeFace (YTF): Following [60], we choose the first 41 subjects of YTF dataset. Faces inside images are first cropped and then resized to 55 by 55 sizes [55]. FRGC: Using the 20 random selected subjects in [60] from the original dataset, we collect 2,462 face images. Similarly, we first crop the face regions and resize them into 32 by 32 images. Table 1 provides a brief description of each dataset.

数据集：为了证明DEPICT适用于多种数据集，我们选择了以下手写数字和人脸图像数据集。考虑到聚类任务完全无监督的特性，在适用情况下我们将训练样本和测试样本合并处理。MNIST-full：包含总计70,000个手写数字的数据集，其中60,000个训练样本和10,000个测试样本，每个样本为32×32单色图像[17]。MNIST-test：仅包含MNIST-full数据集中测试部分的数据集。USPS：来自USPS邮政服务的手写数字数据集，包含11,000个16×16图像样本。CMU-PIE：包含68个人物4种不同表情的32×32人脸图像数据集[43]。YoutubeFace (YTF)：参照[60]，我们选取YTF数据集前41个主体，图像中的人脸先经裁剪后调整为55×55尺寸[55]。FRGC：使用[60]中从原始数据集随机选取的20个主体，共采集2,462张人脸图像。同样地，我们先裁剪人脸区域并调整为32×32图像。表1提供了各数据集的简要说明。

Table 1: Dataset Descriptions

表 1: 数据集描述

数据集	样本数	类别数	维度
MNIST-full	70,000	10	1×28×28
MNIST-test	10,000	10	1×28×28
USPS	11,000	10	1×16×16
FRGC	2,462	20	3×32×32
YTF	10,000	41	3×55×55
CMU-PIE	2,856	68	1×32×32

Clustering Metrics: We have used 2 of the most popular evaluation criteria w