You Only Need One Color Space: An Efficient Network for Low-light Image Enhancement
你只需要一种色彩空间:一种用于低光图像增强的高效网络
Abstract—Low-Light Image Enhancement (LLIE) task tends to restore the details and visual information from corrupted lowlight images. Most existing methods learn the mapping function between low/normal-light images by deep neural networks on sRGB and HSV color space. However, these methods involve sensitivity and instability in the enhancement process, which often generate obvious color and brightness artifacts. To alleviate this problem, we propose a novel trainable color space, named Horizontal/Vertical-Intensity (HVI), which not only decouples brightness and color from RGB channels to mitigate the instability during enhancement, but also adapts to low-light images in different illumination ranges due to the trainable parameters. Furthermore, we design a novel Color and Intensity Decoupling Network (CIDNet) with two branches dedicated to processing the decoupled image brightness and color in the HVI space. In addition, we introduce the Lighten Cross-Attention (LCA) module to facilitate interaction between image structure and content information in both branches, while also suppressing noise in low-light images. We conduct 22 quantitative and qualitative experiments to show that the proposed CIDNet outperforms the state-of-the-art methods on 11 datasets. The code is available at https://github.com/Fediory/HVI-CIDNet.
摘要—低光照图像增强(LLIE)任务旨在从受损的低光照图像中恢复细节和视觉信息。现有方法大多通过在sRGB和HSV色彩空间上训练深度神经网络来学习低光/正常光图像间的映射函数。然而这些方法在增强过程中存在敏感性和不稳定性,常会产生明显的色彩与亮度伪影。为解决该问题,我们提出了一种新型可训练色彩空间HVI (Horizontal/Vertical-Intensity),该空间不仅通过从RGB通道解耦亮度与色彩来缓解增强过程中的不稳定性,还能通过可训练参数适应不同光照范围的低光图像。此外,我们设计了色彩与亮度解耦网络(CIDNet),采用双分支架构在HVI空间中分别处理解耦后的图像亮度和色彩信息。创新性地引入光照交叉注意力(LCA)模块促进双分支间图像结构与内容信息的交互,同时有效抑制低光图像噪声。通过22项定量与定性实验表明,所提出的CIDNet在11个数据集上均优于当前最先进方法。代码已开源:https://github.com/Fediory/HVI-CIDNet。
Index Terms—Low-Light Image Enhancement, HVI Color Space, Transformer, Supervised Learning.
索引术语—低光照图像增强 (Low-Light Image Enhancement)、HVI色彩空间 (HVI Color Space)、Transformer、监督学习 (Supervised Learning)。
I. INTRODUCTION
I. 引言
Under low-light conditions, the sensor captures weak light signals with severe noise, resulting in poor visual quality for low-light images. Obtaining high-quality images from degraded images often necessitates Low-Light Image Enhancement (LLIE), intending to improve the brightness while simultaneously reducing the impact of noise and color bias [1].
在低光照条件下,传感器捕获的光信号微弱且含有严重噪声,导致低光照图像的视觉质量较差。要从退化图像中获取高质量图像,通常需要进行低光照图像增强 (Low-Light Image Enhancement, LLIE) ,旨在提升亮度的同时降低噪声和色偏的影响 [1]。
The majority of existing LLIE approaches [2]–[4] focus on finding an appropriate image brightness, and commonly employ deep neural networks to learn the mapping relationship between low-light images and normal-light images within the sRGB space. However, image brightness and color exhibit a strong interdependence with the three channels in sRGB. A slight disturbance in the color space will cause an obvious variation in both the brightness and color of the generated image. As illustrated in Fig. 1, introducing noise to one dimension (red channel) in the sRGB space dramatically changes the color of the enhanced image. This suggests a mismatch between sRGB space and the low-light enhancement processing, resulting in instability in both brightness and color in the enhanced results. The inherent instability leads to the existing enhancement methods [3], [5] requiring more parameters and complex network architecture to learn this enhancement mapping. It is also why numerous low-light enhancement methods [6], [7] need to incorporate additional brightness and color losses during training.
现有的大多数低光照图像增强(LLIE)方法[2]-[4]专注于寻找合适的图像亮度,通常采用深度神经网络在sRGB色彩空间内学习低光照图像与正常光照图像之间的映射关系。然而,图像亮度与颜色在sRGB空间中与三个通道存在强关联性,色彩空间的轻微扰动会导致生成图像的亮度和颜色发生明显变化。如图1所示,在sRGB空间中对单一维度(红色通道)引入噪声会显著改变增强后图像的颜色。这表明sRGB空间与低光照增强处理之间存在不匹配,导致增强结果在亮度和颜色上都存在不稳定性。这种固有缺陷使得现有增强方法[3][5]需要更多参数和复杂网络架构来学习这种增强映射,也解释了为何众多低光照增强方法[6][7]在训练过程中需要引入额外的亮度和颜色损失函数。
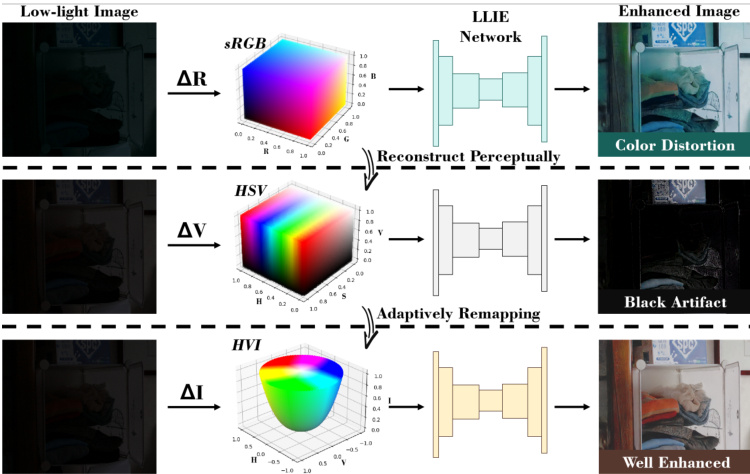
Fig. 1: The sensitivity comparison of different color spaces in lowlight enhancement. The notations $\Delta{\sf R}$ , $\Delta\mathrm{V}_{:}$ , and $\Delta\mathbf{I}$ represent a tiny variation in the axis of Red (sRGB), Value (HSV), and Intensity (HVI), respectively. After enhancement processing, noticeable color artifacts can be observed in the sRGB and HSV space results.
图 1: 不同色彩空间在低光照增强中的敏感性对比。符号$\Delta{\sf R}$、$\Delta\mathrm{V}_{:}$和$\Delta\mathbf{I}$分别表示红轴(sRGB)、明度轴(HSV)和强度轴(HVI)的微小变化。经过增强处理后,在sRGB和HSV空间结果中可观察到明显的色彩伪影。
While the HSV color space [8] enables the separation of brightness and color of the image from sRGB channels, the discontinuous property of hue axis (see Sec. III-B) and its intricate mapping relationships with sRGB space makes it challenging to handle complex and varying lighting conditions. As shown in Fig. 1, enhanced images with the HSV space often have obvious black artifacts due to extremely low light environments. We consider that the color space (e.g., sRGB, HSV) has a huge impact on the image enhancement effect.
虽然HSV色彩空间[8]能够将图像的亮度和颜色从sRGB通道中分离出来,但色相轴的不连续性(见第III-B节)及其与sRGB空间复杂的映射关系,使得处理复杂多变的照明条件具有挑战性。如图1所示,在极低光环境下,使用HSV空间增强的图像常会出现明显的黑色伪影。我们认为色彩空间(如sRGB、HSV)对图像增强效果有重大影响。
To address the aforementioned issue between the low-light image enhancement task and existing color spaces, we introduce a new color space named Horizontal/Vertical-Intensity (HVI), designed specifically to cater to the needs of lowlight enhancement tasks. The proposed HVI color space not only decouples brightness and color information but also incorporates three trainable representation parameters and a trainable function, allowing it to adapt to the brightening scale and color variations of different low-light images. Building upon the HVI color space, to fully leverage the decoupled information, we propose a new LLIE method, named Color and Intensity Decoupling Network (CIDNet). CIDNet consists of HV-branch and intensity-branch, which makes full use of decoupled information to generate high-quality results. After applying the HVI transformation to the image, it is separately fed into the HV-branch to extract color information, and the intensity-branch to establish the photometric mapping function under different lighting conditions. Additionally, to enhance the interaction between the structures of images contained in the brightness and color branches, we propose the bidirectional Lighten Cross-Attention (LCA) module to learn the complementary information of HV-branch and intensity-branch. Furthermore, we conduct experiments and ablation studies on multiple datasets to validate our approach. The experimental results demonstrate that CIDNet effectively enhances the brightness of low-light images while preserving their natural colors, which validates the compatibility of the proposed HVI color space with low-light image enhancement tasks. Note that the proposed method exhibits relatively small parameters (1.88M) and computational loads (7.57G), achieving a good balance between effectiveness and efficiency on edge devices. Our contributions can be summarized as follows:
为解决低光照图像增强任务与现有色彩空间之间的上述问题,我们提出了一种名为水平/垂直-亮度(HVI)的新型色彩空间,专为满足低光照增强任务需求而设计。所提出的HVI色彩空间不仅能解耦亮度和色彩信息,还包含三个可训练表示参数和一个可训练函数,使其能适应不同低光照图像的亮度尺度与色彩变化。基于HVI色彩空间,为充分利用解耦信息,我们提出了一种新的低光照图像增强方法——色彩与亮度解耦网络(CIDNet)。CIDNet由HV分支和亮度分支组成,通过充分运用解耦信息生成高质量结果。图像经HVI转换后,分别输入HV分支提取色彩信息,以及亮度分支建立不同光照条件下的光度映射函数。此外,为增强亮度与色彩分支所含图像结构间的交互,我们提出了双向光照交叉注意力(LCA)模块来学习HV分支与亮度分支的互补信息。我们在多个数据集上进行了实验与消融研究以验证方法有效性。实验结果表明,CIDNet在提升低光照图像亮度的同时能保持自然色彩,验证了HVI色彩空间与低光照增强任务的兼容性。值得注意的是,该方法参数量(1.88M)和计算量(7.57G)相对较小,在边缘设备上实现了效果与效率的良好平衡。我们的贡献可总结如下:
II. RELATED WORK
II. 相关工作
A. Low-Light Image Enhancement
A. 低光照图像增强
Traditional and Plain LLIE Methods. Plain methods usually enhanced image by histogram equalization [9] and Gama Corrction [10]. Traditional method [11] commonly depends on the application of the Retinex theory, which decomposes the lights into illumination and reflections. For example, Guo et al. [12] refine the initial illumination map to optimize lighting details by imposing a structure prior. Regrettably, existing methodologies are inadequate in effectively eliminating noise artifacts and producing accurate color mappings, rendering them incapable of achieving the desired level of precision and finesse in the LLIE tasks.
传统与朴素低光照图像增强方法。朴素方法通常通过直方图均衡化[9]和伽马校正[10]来增强图像。传统方法[11]普遍基于Retinex理论,将光线分解为照度与反射分量。例如Guo等[12]通过引入结构先验来优化初始照度图以提升光照细节。遗憾的是,现有方法在有效消除噪声伪影和生成精确色彩映射方面存在不足,导致其无法达到低光照增强任务所需的精度与细腻度。
Deep Learning Methods. Deep learning-based approaches [2], [3], [13], [14] has been widely used in LLIE task. Existing methods propose distinct solutions to address the issues of image color shift and noise stabilization. For instance, RetinexNet [6] enhances images by decoupling illumination and reflectance based on Retinex theory. However, it has unsatisfied results with several color shifts. SNR-Aware [15] presents a collectively exploiting Signal-to-Noise-Ratioaware transformers to dynamically enhance pixels with spatialvarying operations, which could reduce the color bias and noise. Bread [8] decouples the entanglement of noise and color distortion by using YCbCr color space. Furthermore, they designed a color adaption network to tackle the color distortion issue left in light-enhanced images. Still, SNRAware and Bread show poor generalization ability. They are not only inaccurately controlled in terms of brightness in some of the datasets, but also biased in terms of color with pure black area.
深度学习方法。基于深度学习的方法 [2]、[3]、[13]、[14] 已被广泛应用于低光照图像增强 (LLIE) 任务。现有方法针对图像色偏和噪声稳定问题提出了不同解决方案。例如,RetinexNet [6] 基于Retinex理论通过解耦光照与反射率来增强图像,但存在明显色偏问题。SNR-Aware [15] 提出利用信噪比感知 (Signal-to-Noise-Ratioaware) Transformer 动态执行空间可变像素增强,可减少色彩偏差和噪声。Bread [8] 通过YCbCr色彩空间解耦噪声与色彩失真,并设计色彩适应网络处理增强图像的残留色偏问题。然而SNR-Aware和Bread的泛化能力较差,不仅在部分数据集中存在亮度控制失准问题,对纯黑区域还会产生色彩偏差。
Diffusion Model-based Methods. With the advancement of Denoising Diffusion Probabilistic Models (DDPMs) [16], diffusion-based generative models have achieved remarkable results in the LLIE task. It has indeed shown the capability to generate more accurate and appropriate images in pure black spaces devoid of information and under low light conditions with significant noise. However, they still exhibit issues such as local overexposure or color shift. Recent LLIE diffusion methods have attempted to address these challenges by incorporating global supervised brightness correction or employing local color correctors [17]–[19]. PyDiff [17] employs a Global Feature Modulation to correct the pixel noise and color bias globally. Diff-Retinex [20] rethink the retinex theory with a diffusion-based model in the LLIE task, which decomposed an image to illumination and reflectance colors to reduce color bias and enhance brightness separately. However, the aforementioned diffusion models suffer from long training and inference times, lack of Lighten efficiency, and inability to fully decouple brightness and color information.
基于扩散模型的方法。随着去噪扩散概率模型 (Denoising Diffusion Probabilistic Models, DDPM) [16] 的发展,基于扩散的生成模型在低光照图像增强 (LLIE) 任务中取得了显著成果。该模型确实展现了在纯黑无信息空间及强噪声低光条件下生成更准确、更合适图像的能力,但仍存在局部过曝或色偏等问题。近期基于扩散的LLIE方法尝试通过引入全局监督亮度校正或采用局部色彩校正器 [17]–[19] 来解决这些挑战。PyDiff [17] 采用全局特征调制 (Global Feature Modulation) 来全局校正像素噪声和色彩偏差。Diff-Retinex [20] 在LLIE任务中以扩散模型重新思考Retinex理论,将图像分解为光照分量和反射分量以分别降低色偏并增强亮度。然而上述扩散模型仍存在训练推理耗时长、提亮效率不足、无法完全解耦亮度与色彩信息等缺陷。
B. Color Space
B. 色彩空间
RGB. Currently, the most commonly used is the standardRGB (sRGB) color space. For the same principle as visual recognition by the human eye, sRGB is widely used in digital imaging devices [21]. Nevertheless, image brightness and color exhibit a strong interdependence with the three channels in sRGB. A slight disturbance in the color space will cause an obvious variation in both the brightness and color of the generated image. Thus, sRGB is not the optimal color space for enhancement.
RGB。目前最常用的是标准RGB (sRGB) 色彩空间。由于与人眼视觉识别原理相同,sRGB被广泛应用于数字成像设备 [21]。然而,在sRGB中图像亮度与色彩三个通道存在强关联性,色彩空间的轻微扰动会导致生成图像的亮度和色彩发生明显变化。因此,sRGB并非图像增强的最佳色彩空间。
HSV and YCbCr. Hue, Saturation and Value (HSV) color space represents points in an RGB color model with a cylindrical coordinate system [22]. Indeed, it does decouple brightness and color of the image from RGB channels. However, the inherent hue axis color discontinuity and non-mono-mapped pure black planes pose significant challenges when attempting to enhance the image in HSV color space, resulting in the emergence of obvious artifacts. To circumvent issues related to HSV, some methods [8], [23] also transform sRGB images to the YCbCr color space for processing, which has an illumination axis (Y) and reflect-color-plain (CbCr). Although it solved the hue dimension discontinuity problem of HSV, the multi-mapping of pure black planes still exists.
HSV 和 YCbCr。色调、饱和度和明度 (HSV) 色彩空间通过柱坐标系表示 RGB 色彩模型中的点 [22]。它确实将图像的亮度和颜色与 RGB 通道解耦,但其固有的色调轴颜色不连续性及非单映射纯黑平面在 HSV 色彩空间中进行图像增强时会带来显著挑战,导致明显伪影的出现。为避免 HSV 相关问题,部分方法 [8][23] 也会将 sRGB 图像转换至 YCbCr 色彩空间处理,该空间包含亮度轴 (Y) 和反射色平面 (CbCr)。尽管它解决了 HSV 的色调维度不连续问题,但纯黑平面的多重映射现象仍然存在。
III. HVI COLOR SPACE
III. HVI 色彩空间
To address the misalignment between LLIE and existing color spaces, we innovative ly introduce a trainable color space in the field of LLIE, named Horizontal/Vertical-Intensity (HVI) color space. HVI color space consists of three trainable parameters and a custom training function that can adapt to the photosensitive characteristics and color sensitivities of lowlight images. In this section, we will present the description of the mono-mapping image transformation from sRGB space to HVI color space, as well as the details of HVI color space.
为解决低光照图像增强(LLIE)与现有色彩空间不匹配的问题,我们创新性地在LLIE领域引入了一种可训练的色彩空间,命名为水平/垂直-强度(HVI)色彩空间。HVI色彩空间由三个可训练参数和一个自定义训练函数组成,能够适应低光照图像的光敏特性和色彩敏感度。本节将详细介绍从sRGB空间到HVI色彩空间的单映射图像转换方法,以及HVI色彩空间的具体细节。
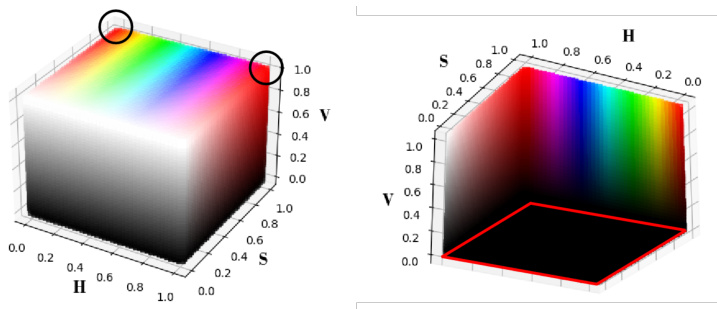
Fig. 2: HSV color space visualization. The two black circles in the left image indicate the discontinuous color positions along the hue axis, while the red box in the right image displays a pure black plane with Value $=0$ .
图 2: HSV色彩空间可视化。左图中的两个黑色圆圈表示沿色调轴的不连续颜色位置,而右图中的红色框显示了一个纯黑色平面,其亮度值 $=0$。
A. Intensity Map
A. 强度图
In the task of LLIE, one crucial aspect is accurately estimating the illumination intensity map of the scene. Following retinex-based LLIE methods [6], [7], [12], we represent the intensity map of an image with the maximum value among the RGB channels. According to the definition, we can calculate the intensity map of an image $\mathbf{I}_{m a x}\in\mathbb{R}^{\mathrm{H}\times\mathrm{W}\times3}$ as follows:
在LLIE任务中,一个关键环节是准确估计场景的照明强度图。基于Retinex理论的LLIE方法[6][7][12],我们使用RGB通道中的最大值来表示图像的强度图。根据定义,图像强度图$\mathbf{I}_{m a x}\in\mathbb{R}^{\mathrm{H}\times\mathrm{W}\times3}$的计算方式如下:
$$
\mathbf{I}{m a x}=\operatorname*{max}{\mathbf{c}\in{R,G,B}}(\mathbf{I_{c}}),
$$
$$
\mathbf{I}{m a x}=\operatorname*{max}{\mathbf{c}\in{R,G,B}}(\mathbf{I_{c}}),
$$
Next, we will introduce how to utilize the intensity map to guide the generation of the corresponding HV color map.
接下来,我们将介绍如何利用强度图来指导生成相应的HV彩色图。
B. HV Transformation
B. HV 变换
To effectively address color deviations, previous LLIE methods typically separate an sRGB image into a reflectance map [2], [6] based on the retinex theory. These approaches often require a large computational network for fitting, which need to use a combination of hue and saturation to simulate the reflectance map. However, the HSV color space is discontinued in the hue axis (see the black circles in Fig. 2) and has a non-bijection pure black plane (see the red rectangle in Fig. 2), which disrupts the one-to-one mapping. For discontinuity of the hue axis, based on HSV color transform formula, a red color in sRGB $(R,G,B)=(1,0,0)$ corresponds to $(0,1,1)$ and $(1,1,1)$ in HSV color space. For the pure black plane, as shown in Fig. 2, any HSV pixel with Value $=~0$ denote the black color, corresponding to $(R,G,B)=(0,0,0)$ in sRGB color space. Thus, the one-to-many mapping is the source reason of why the existing methods on HSV color space generate the obvious artifacts in the dark regions.
为有效解决色彩偏差问题,现有LLIE方法通常基于视网膜反射理论将sRGB图像分解为反射率图[2][6]。这类方法往往需要庞大的计算网络进行拟合,需结合色调与饱和度来模拟反射率图。然而HSV色彩空间的色调轴存在不连续性(见图2中黑色圆圈),且存在非双射的纯黑平面(见图2中红色矩形),破坏了一对一映射关系。针对色调轴不连续性问题,根据HSV色彩转换公式,sRGB中的红色$(R,G,B)=(1,0,0)$对应HSV色彩空间中的$(0,1,1)$和$(1,1,1)$;对于纯黑平面,如图2所示,任何Value$=~0$的HSV像素均表示黑色,对应sRGB色彩空间的$(R,G,B)=(0,0,0)$。这种一对多映射关系正是现有HSV色彩空间方法在暗区产生明显伪影的根本原因。
To address the suboptimum problems caused by one-tomany mapping (HSV color space), we design a trainable Horizonal/Vertical (HV) color map as a plane to quantify a color-reflectance map, which is a one-to-one mapping to sRGB color space. The HVI color space consists of three trainable parameters $k$ , $\gamma_{G}$ and $\gamma_{B}$ , and a custom training function $T(x)$ .
为了解决一对多映射(HSV色彩空间)导致的次优问题,我们设计了一个可训练的横向/纵向(HV)色彩映射平面来量化色彩-反射率映射,该平面与sRGB色彩空间形成一对一映射关系。HVI色彩空间包含三个可训练参数$k$、$\gamma_{G}$和$\gamma_{B}$,以及一个自定义训练函数$T(x)$。
Parameter $k$ . Considering that the dark regions of lowlight images have small values, which is hard to distinguish the color and causes information loss. Based on the proposed HVI color space, we customize a parameter $k$ that allows networks to adjust the color point density of the low-intensity color plane, which quantifies a Color-Density $k$ $\left(\mathbf{C}_{k}\right)$ as
参数 $k$。考虑到低光图像的暗区数值较小,难以区分颜色并导致信息丢失。基于提出的HVI色彩空间,我们定制了一个参数 $k$,使网络能够调整低强度色彩平面的色点密度,并将其量化为色彩密度 $k$ $\left(\mathbf{C}_{k}\right)$。
$$
\mathbf{C}{k}=\sqrt[k]{\sin(\frac{\pi\mathbf{I}_{m a x}}{2})+\varepsilon},
$$
$$
\mathbf{C}{k}=\sqrt[k]{\sin(\frac{\pi\mathbf{I}_{m a x}}{2})+\varepsilon},
$$
where $k\in\mathbb{Q}^{+}$ and we set $\varepsilon=1\times10^{-8}$ .
其中 $k\in\mathbb{Q}^{+}$ 且设 $\varepsilon=1\times10^{-8}$。
Hue bias parameter $\gamma_{G}$ and $\gamma_{B}$ . Since different cameras have different sensitivity on RGB channel, it will cause color shift (i.e. green color) on the low-light scenes. To alleviate the data diversity caused by color shift, we learn an adaptive linear Color-Perceptual map $\mathbf{P}_{\gamma}$ on hue value.
色调偏差参数 $\gamma_{G}$ 和 $\gamma_{B}$。由于不同相机对RGB通道的敏感度不同,会导致低光场景出现色彩偏移(如偏绿色)。为缓解色彩偏移造成的数据多样性,我们在色调值上学习了一个自适应线性色彩感知映射 $\mathbf{P}_{\gamma}$。
where $\gamma_{G},\gamma_{B}\in(0,1)$ , $\mathbf{H}\in[0,1]$ denotes the hue value.
其中 $\gamma_{G},\gamma_{B}\in(0,1)$ , $\mathbf{H}\in[0,1]$ 表示色调值。
Customizable or trainable function $T(x)$ . To improve the saturation the generated results, we design a Function-Density $T$ based on the $\mathbf{P}_{\gamma}$ to adaptively adjust the saturation. We utilize a Function-Density $T$ as
可定制或可训练函数 $T(x)$ 。为了提升生成结果的饱和度,我们基于 $\mathbf{P}_{\gamma}$ 设计了一个函数密度 $T$ 来自适应调整饱和度。具体采用函数密度 $T$ 的形式为
$$
\begin{array}{r}{\mathbf{D}{T}=T(\mathbf{P}_{\gamma}),}\end{array}
$$
$$
\begin{array}{r}{\mathbf{D}{T}=T(\mathbf{P}_{\gamma}),}\end{array}
$$
where $T(\cdot)$ satisfies $T(0)=T(1)$ and $T(\mathbf{P}_{\gamma})\geq0$ . Finally, we formalize the horizontal $(\hat{\mathbf{H}})$ and vertical $(\hat{\mathbf{V}})$ plane as
其中 $T(\cdot)$ 满足 $T(0)=T(1)$ 且 $T(\mathbf{P}_{\gamma})\geq0$。最终,我们将水平面 $(\hat{\mathbf{H}})$ 和垂直面 $(\hat{\mathbf{V}})$ 形式化为
$$
\begin{array}{r}{\hat{\mathbf{H}}=\mathbf{C}{k}\odot\mathbf{S}\odot\mathbf{D}{T}\odot h,}\ {\hat{\mathbf{V}}=\mathbf{C}{k}\odot\mathbf{S}\odot\mathbf{D}_{T}\odot v,}\end{array}
$$
$$
\begin{array}{r}{\hat{\mathbf{H}}=\mathbf{C}{k}\odot\mathbf{S}\odot\mathbf{D}{T}\odot h,}\ {\hat{\mathbf{V}}=\mathbf{C}{k}\odot\mathbf{S}\odot\mathbf{D}_{T}\odot v,}\end{array}
$$
where $\odot$ denotes the element-wise multiplication. Note that we orthogonal ize our color map by setting an intermediate variable $h=\cos(2\pi\mathbf{P}{\gamma})$ and $v=\sin(2\pi\mathbf{P}_{\gamma})$ to be bijective.
其中 $\odot$ 表示逐元素相乘。注意,我们通过设置中间变量 $h=\cos(2\pi\mathbf{P}{\gamma})$ 和 $v=\sin(2\pi\mathbf{P}_{\gamma})$ 使颜色映射双射正交化。
C. Perceptual-invert HVI Transformation
C. 感知可逆的HVI变换
To convert HVI back to the HSV color space, we design a Perceptual-invert HVI Transformation (PHVIT), which is a surjective mapping while allowing for the independent adjustment of the image’s saturation and brightness.
为了将HVI转换回HSV色彩空间,我们设计了一种感知可逆的HVI变换(PHVIT),这是一种满射映射,同时允许独立调整图像的饱和度和亮度。
To transform injective ly, the PHVIT sets $\hat{h}$ and $\hat{v}$ as an intermediate variable as
为了进行单射变换,PHVIT将$\hat{h}$和$\hat{v}$设为中间变量
$$
\hat{h}=\frac{\hat{\mathbf{I}}{\mathbf{H}}}{\mathbf{D}{T}\mathbf{C}{k}+\varepsilon},\hat{v}=\frac{\hat{\mathbf{I}}{\mathbf{V}}}{\mathbf{D}{T}\mathbf{C}_{k}+\varepsilon},
$$
$$
\hat{h}=\frac{\hat{\mathbf{I}}{\mathbf{H}}}{\mathbf{D}{T}\mathbf{C}{k}+\varepsilon},\hat{v}=\frac{\hat{\mathbf{I}}{\mathbf{V}}}{\mathbf{D}{T}\mathbf{C}_{k}+\varepsilon},
$$
where $\varepsilon=1\times10^{-8}$ . Then, we convert $\hat{h}$ and $\hat{v}$ to HSV color space. The hue map can be formulated by
其中 $\varepsilon=1\times10^{-8}$。接着,我们将 $\hat{h}$ 和 $\hat{v}$ 转换到 HSV 色彩空间。色调图可通过以下公式表示:
$$
H=F_{\gamma}(\arctan(\frac{\hat{v}}{\hat{h}})\mod1),
$$
$$
H=F_{\gamma}(\arctan(\frac{\hat{v}}{\hat{h}})\mod1),
$$
where $F_{\gamma}$ is a inverse linear function as
其中 $F_{\gamma}$ 是一个反线性函数,形式为
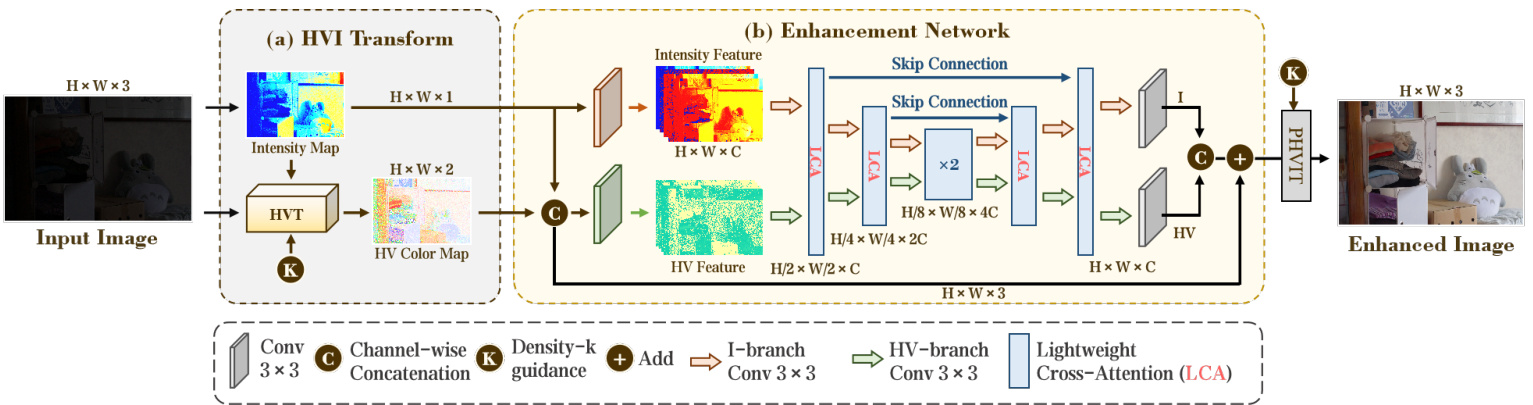
Fig. 3: The overview of the proposed CIDNet. (a) HVI Color Transformation (HVIT) takes an sRGB image as input and generates HV color map and intensity map as outputs. (b) Enhancement Network performs the main processing, utilizing a dual-branch UNet architecture, which contains six Lighten Cross-Attention (LCA) blocks. Lastly, we apply Perceptual-inverse HVI Transform (PHVIT) to take a light-up HVI map as input and transform it into an sRGB-enhanced image.
图 3: 提出的CIDNet框架概览。(a) HVI色彩变换(HVIT)以sRGB图像作为输入,生成HV色彩图和亮度图作为输出。(b) 增强网络采用双分支UNet架构进行核心处理,包含六个轻量化交叉注意力(LCA)模块。最后通过感知逆HVI变换(PHVIT)将提亮后的HVI映射转换为增强的sRGB图像。
where $\gamma_{G},\gamma_{B}$ are mentioned in Eq. 3. The saturation and value map can be perceptual ly estimated as
其中 $\gamma_{G},\gamma_{B}$ 在公式3中已提及。饱和度和明度图可通过感知方式估算为
$$
\begin{array}{l}{{S=\alpha_{S}\sqrt{\hat{h}^{2}+\hat{v}^{2}},}}\ {{V=\alpha_{I}\hat{\bf I}_{\bf I},}}\end{array}
$$
$$
\begin{array}{l}{{S=\alpha_{S}\sqrt{\hat{h}^{2}+\hat{v}^{2}},}}\ {{V=\alpha_{I}\hat{\bf I}_{\bf I},}}\end{array}
$$
where $\alpha_{s},\alpha_{i}$ are the customizing linear parameters to change the image color saturation and brightness. Finally, we will obtain the sRGB image with HSV image [22].
其中 $\alpha_{s},\alpha_{i}$ 是用于调整图像色彩饱和度(saturation)和亮度(brightness)的自定义线性参数。最终我们将获得带有HSV图像[22]的sRGB图像。
IV. CIDNET
IV. CIDNET
Based on the proposed HVI space, we introduce a novel dual-branch LLIE network, named the Color and Intensity Decoupling Network (CIDNet) to separately address HV-plain and I-axis information in the HVI space. The CIDNet employs HV-branch to suppress the noise and chromatic it y in the dark regions and utilizes I-branch to estimate the luminance of the whole images. Furthermore, we design an Lighten CrossAttention (LCA) module to facilitate interaction guidance between the HV-branch and I-branch. In this section, we provide a detailed description of the architecture of CIDNet.
基于提出的HVI空间,我们引入了一种新颖的双分支低光照图像增强网络,称为色彩与亮度解耦网络(CIDNet),用于分别处理HVI空间中的HV平面和I轴信息。CIDNet采用HV分支抑制暗区的噪声和色度,利用I分支估计整幅图像的亮度。此外,我们设计了轻量交叉注意力(LCA)模块来促进HV分支与I分支之间的交互引导。本节将详细描述CIDNet的网络架构。
A. Pipeline
A. 流水线
As shown in Fig. 3, the overall framework can be divided into three consecutive main steps, i.e., HVI transformation, enhancement network, and perceptual-inverse HVI transformation.
如图 3 所示,整体框架可分为三个连续的主要步骤,即 HVI 转换、增强网络和感知逆 HVI 转换。
As described in Sec. III, the HVI transformation decomposes the sRGB image into two components: an intensity map containing scene ill umi nance information and an HV color map containing scene color and structure information. Specifically, we first calculate the intensity map using Eq. 1, which is ${\mathbf{I}}{\mathbf{I}}={\mathbf{I}}_{m a x}$ . Subsequently, we utilize the intensity map and the original image to generate HV color map using Eq. 5. Furthermore, a trainable density $k$ is employed to adjust the color point density of the low-intensity color plane, as shown in Fig. 3(a).
如第 III 节所述,HVI 变换将 sRGB 图像分解为两个分量:包含场景照度信息的强度图 (intensity map) 和包含场景颜色与结构信息的 HV 色彩图 (HV color map)。具体而言,我们首先通过公式 1 计算强度图 ${\mathbf{I}}{\mathbf{I}}={\mathbf{I}}_{m a x}$,随后利用强度图和原始图像通过公式 5 生成 HV 色彩图。此外,如图 3(a) 所示,我们采用可训练密度参数 $k$ 来调节低强度色彩平面的色点密度。
Based on the UNet architecture, the enhancement network takes an intensity map and HV color map as input. To learn the initial information of intensity map and HV color map, we employ $3\times3$ convolutional layers to obtain the features with same dimension in each branch. Subsequently, the features are fed into the UNet with Lighten Cross-Attention (LCA) modules. The LCA module consists of cross attention blocks, color denoise layer and intensity enhance layer. The cross attention block learns the corresponding interacted information between the HV-branch and I-branch. The color denoise layer avoids noise artifacts and color shift, and the intensity enhance layer improves the luminance and removes the saturated regions. The final outputs of UNet are the refined intensity and HV maps. To decrease the difficulty of the learning process, we employ a residual mechanism to add the original HVI map. Finally, we perform an HVI inverse transformation with the trainable parameter density $k$ to map the image to the sRGB space.
基于UNet架构的增强网络以强度图和HV彩色图作为输入。为学习强度图和HV彩色图的初始信息,我们采用$3\times3$卷积层在各分支中获取相同维度的特征。随后,这些特征被输入带有轻量交叉注意力(LCA)模块的UNet网络。LCA模块由交叉注意力块、色彩降噪层和强度增强层组成:交叉注意力块学习HV分支与I分支间的交互信息;色彩降噪层避免噪声伪影和色偏;强度增强层提升亮度并消除饱和区域。UNet的最终输出是优化后的强度图和HV图。为降低学习难度,我们采用残差机制叠加原始HVI图。最后通过可训练参数密度$k$进行HVI逆变换,将图像映射至sRGB色彩空间。
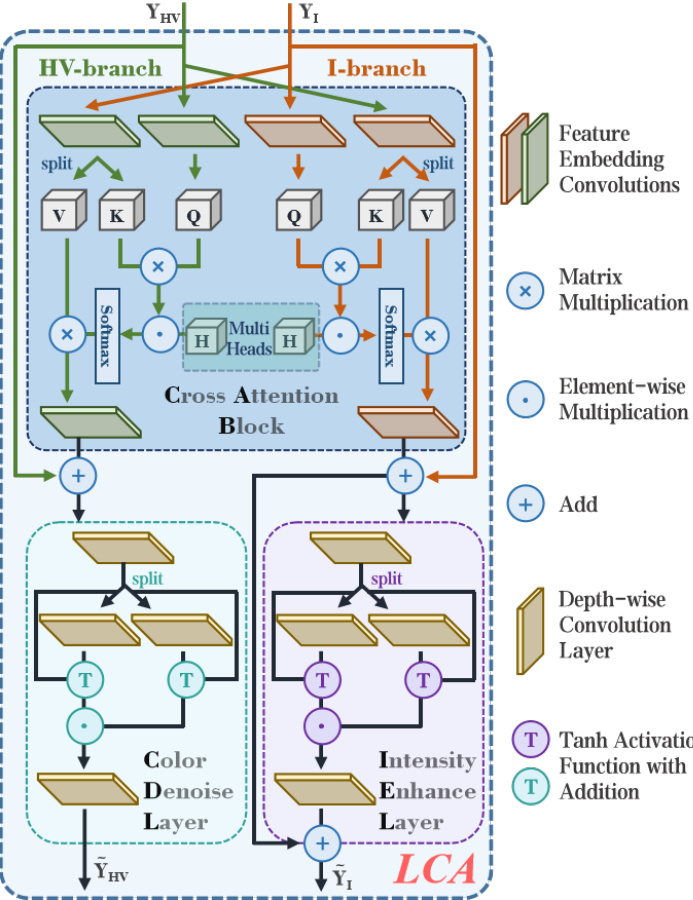
Fig. 4: The dual-branch Lighten Cross-Attention (LCA) block (i.e., I-branch and HV-branch). The LCA incorporates a Cross Attention Block (CAB), an Intensity Enhance Layer (IEL), and a Color Denoise Layer (CDL). The feature embedding convolution layers contains a $1\times1$ depth-wise convolution and a $3\times3$ group convolution.
图 4: 双分支轻量化交叉注意力 (LCA) 模块 (即 I 分支和 HV 分支)。该模块包含交叉注意力块 (CAB)、强度增强层 (IEL) 和色彩降噪层 (CDL)。特征嵌入卷积层由 $1\times1$ 深度可分离卷积和 $3\times3$ 分组卷积构成。

Fig. 5: Visual comparisons of the enhanced results by different methods on LOLv1 and LOLv2. (Zoom in for the best view.)
图 5: 不同方法在 LOLv1 和 LOLv2 数据集上的增强效果视觉对比。(建议放大查看最佳效果)
B. Structure
B. 结构
- Enhancement Network: As depicted in Fig. 3(b), we use the commonly employed UNet as the baseline network, which has an encoder, decoder, and multiple skip connections. The encoder includes three LCA blocks and downsample and $3\times3$ kernel convolutional layers. Similarly, the decoder consists of three LCA modules, and upsampling layers.
- 增强网络:如图 3(b) 所示,我们采用常用的 UNet 作为基线网络,该网络包含编码器、解码器和多个跳跃连接。编码器包含三个 LCA 块、下采样层和 $3\times3$ 核卷积层。类似地,解码器由三个 LCA 模块和上采样层构成。
- Lighten Cross-Attention: To enhance the interaction between the structures of images contained in the brightness and color branches, we propose the Lighten Cross-Attention (LCA) module to learn the complementary information of HV-branch and intensity-branch. As shown in Fig. 4, the HV-branch and I-branch in LCA handle HV features and intensity features, respectively. To learn the complementary potential between HV features and intensity features during the processing, we propose cross attention block (CAB) to facilitate mutual guidance between HV features and intensity features. To force the CAB to learn the information from the opposite branch (i.e., HV branch only use the information of I-brach to refine itself), we utilize the one branch as the query and leverage another branch as key and value in the CAB.
- Lighten Cross-Attention:为增强亮度分支与色彩分支中图像结构的交互,我们提出Lighten Cross-Attention (LCA) 模块来学习HV分支与强度分支的互补信息。如图4所示,LCA中的HV分支和I分支分别处理HV特征与强度特征。为在学习过程中挖掘HV特征与强度特征的互补潜力,我们提出交叉注意力块 (CAB) 来促进两种特征间的相互引导。为确保CAB仅从对立分支学习信息 (即HV分支仅利用I分支信息优化自身),我们在CAB中将一个分支作为query,另一个分支作为key和value。
As shown in 4, The CAB exhibits a symmetrical structure between the I-way and HV-way. We use the I-branch as an example to describe the details. $\mathbf{Y_{I}}\in\mathbb{R}^{\hat{H}\times\hat{W}\times\hat{C}}$ denotes the inputs of I-branch, our CAB first derives query $\mathbf{\Psi}^{(\mathbf{Q})}$ by $\mathbf{Q}=$ $W^{(Q)}\mathbf{Y_{I}}$ . Meanwhile, the CAB splits key $(\mathbf{K})$ and value $(\mathbf{V})$ by $\mathbf{K}=W^{(K)}\mathbf{Y_{I}}$ and $\mathbf{V} =~{\bar{W}}^{(V)}\mathbf{Y_{I}}$ . $W^{(Q)}$ , $W^{(K)}$ and $\dot{W}^{(V)}$ represents the feature embedding convolution layers. We formulate as
如图4所示,CAB在I-way和HV-way之间呈现出对称结构。我们以I-branch为例说明细节。$\mathbf{Y_{I}}\in\mathbb{R}^{\hat{H}\times\hat{W}\times\hat{C}}$表示I-branch的输入,我们的CAB首先通过$\mathbf{Q}=$$W^{(Q)}\mathbf{Y_{I}}$生成查询$\mathbf{\Psi}^{(\mathbf{Q})}$。同时,CAB通过$\mathbf{K}=W^{(K)}\mathbf{Y_{I}}$和$\mathbf{V} =~{\bar{W}}^{(V)}\mathbf{Y_{I}}$拆分键$(\mathbf{K})$与值$(\mathbf{V})$。$W^{(Q)}$、$W^{(K)}$和$\dot{W}^{(V)}$代表特征嵌入卷积层。我们将其表述为
$$
{\hat{\mathbf{Y}}}{\mathbf{I}}=W(\mathbf{V}\otimes\operatorname{Softmax}\left(\mathbf{Q}\otimes\mathbf{K}/\alpha_{H}\right)+\mathbf{Y}_{\mathbf{I}})
$$
$$
{\hat{\mathbf{Y}}}{\mathbf{I}}=W(\mathbf{V}\otimes\operatorname{Softmax}\left(\mathbf{Q}\otimes\mathbf{K}/\alpha_{H}\right)+\mathbf{Y}_{\mathbf{I}})
$$
where $\alpha_{H}$ is the multi-head factor [24] and $W(\cdot)$ denotes the feature embedding convolutions.
其中 $\alpha_{H}$ 是多头因子 [24],$W(\cdot)$ 表示特征嵌入卷积。
Next, following Retinex theory, intensity enhance layer (IEL) decomposes the tensor $\hat{\mathbf{Y_{I}}}$ as $\mathbf{Y}{I}{\dot{\mathbf{\theta}}}=\mathbf{\theta}W^{(I)}{\hat{\mathbf{Y}}}{\mathbf{I}}$ and $\mathbf{Y}{R}=W^{(R)}\bar{\hat{\mathbf{Y}}}_{\mathbf{I}}$ . The IEL is defined as
接下来,根据Retinex理论,强度增强层(IEL)将张量$\hat{\mathbf{Y_{I}}}$分解为$\mathbf{Y}{I}{\dot{\mathbf{\theta}}}=\mathbf{\theta}W^{(I)}{\hat{\mathbf{Y}}}{\mathbf{I}}$和$\mathbf{Y}{R}=W^{(R)}\bar{\hat{\mathbf{Y}}}_{\mathbf{I}}$。IEL定义为
$$
\begin{array}{r}{\tilde{\mathbf{Y}}{\mathbf{I}}=W_{s}((\operatorname{tanh}{(W_{s}\mathbf{Y}{I})}+\mathbf{Y}{I})\quad}\ {\odot(\operatorname{tanh}{(W_{s}\mathbf{Y}{R})}+\mathbf{Y}_{R}))}\end{array}
$$
$$
\begin{array}{r}{\tilde{\mathbf{Y}}{\mathbf{I}}=W_{s}((\operatorname{tanh}{(W_{s}\mathbf{Y}{I})}+\mathbf{Y}{I})\quad}\ {\odot(\operatorname{tanh}{(W_{s}\mathbf{Y}{R})}+\mathbf{Y}_{R}))}\end{array}
$$
where $\odot$ represents the element-wise multiplication and $W_{s}$ denotes the depth-wise convolution layers. Finally, the output of IEL adds the residuals to simplify the training process.
其中 $\odot$ 表示逐元素相乘,$W_{s}$ 表示深度卷积层。最终,IEL (Intra-Encoder Layer) 的输出通过添加残差来简化训练过程。
C. Loss Function
C. 损失函数
To integrate the advantages of HVI space and the sRGB space, the loss function consists both color spaces. In HVI color space, we utilize L1 loss $L_{1}$ , edge loss $L_{e}$ [25], and perceptual loss $L_{p}$ [26] for the low-light enhancement task. It can be expressed as
为了整合HVI空间和sRGB空间的优势,损失函数同时包含这两个色彩空间。在HVI色彩空间中,我们采用L1损失$L_{1}$、边缘损失$L_{e}$[25]以及感知损失$L_{p}$[26]来完成低光增强任务。其表达式为
$$
\begin{array}{r}{l(\hat{X}{H V I},X_{H V I})=\lambda_{1}\cdot L_{1}(\hat{X}{H V I},X_{H V I})}\ {+\lambda_{e}\cdot L_{e}(\hat{X}{H V I},X_{H V I}),}\ {+\lambda_{p}\cdot L_{p}(\hat{X}{H V I},X_{H V I})}\end{array}
$$
$$
\begin{array}{r}{l(\hat{X}{H V I},X_{H V I})=\lambda_{1}\cdot L_{1}(\hat{X}{H V I},X_{H V I})}\ {+\lambda_{e}\cdot L_{e}(\hat{X}{H V I},X_{H V I}),}\ {+\lambda_{p}\cdot L_{p}(\hat{X}{H V I},X_{H V I})}\end{array}
$$
where $\lambda_{1},\lambda_{e},\lambda_{p}$ are all the weight to trade-off the loss function $l(\cdot)$ . In sRGB color space, we employ the same loss function as $l(\hat{I},I)$ . Therefore, our overall loss function $L$ is represented by
其中 $\lambda_{1},\lambda_{e},\lambda_{p}$ 均为权衡损失函数 $l(\cdot)$ 的权重。在 sRGB 色彩空间中,我们采用与 $l(\hat{I},I)$ 相同的损失函数。因此,我们的总体损失函数 $L$ 可表示为
$$
\boldsymbol{L}=\lambda_{c}\cdot\boldsymbol{l}(\hat{\mathbf{I}}{\mathbf{HVI}},\mathbf{I}_{\mathbf{HVI}})+\boldsymbol{l}(\hat{\mathbf{I}},\mathbf{I})
$$
$$
\boldsymbol{L}=\lambda_{c}\cdot\boldsymbol{l}(\hat{\mathbf{I}}{\mathbf{HVI}},\mathbf{I}_{\mathbf{HVI}})+\boldsymbol{l}(\hat{\mathbf{I}},\mathbf{I})
$$
where $\lambda_{c}$ is the weight to balance the loss in different color spaces.
其中 $\lambda_{c}$ 是用于平衡不同色彩空间中损失的权重。
V. EXPERIMENTS
V. 实验
A. Datasets and Settings
A. 数据集与设置
We employ seven commonly-used LLIE benchmark datasets for evaluation, including LOLv1 [6], LOLv2 [27], DICM [28], LIME [12], MEF [29], NPE [30], and VV [31]. We also conduct further experiments on two extreme datasets, SICE [32] (containing mix and grad test sets [33]) and SID (SonyTotal-Dark) [34]. Since blurring is often prone to occur in low-luminosity images, to demonstrate the robustness of our CIDNet to multitasking, we conducted experiments on LOLBlur [35] as well.
我们采用七个常用低光照图像增强(LLIE)基准数据集进行评估,包括LOLv1 [6]、LOLv2 [27]、DICM [28]、LIME [12]、MEF [29]、NPE [30]和VV [31]。还在两个极端数据集SICE [32](包含mix和grad测试集[33])和SID(SonyTotal-Dark) [34]上进行了补充实验。由于低光照图像容易产生模糊现象,为验证CIDNet在多任务处理中的鲁棒性,我们同时在LOLBlur [35]数据集上进行了实验。
TABLE I: Quantitative comparisons $\mathrm{PSNR/SSIM\uparrow}$ on LOL (v1 and v2) datasets. Normal and GT Mean represent with and without gammacorrected by Ground Truth. The highest result is in red color, the second highest result is in cyan color, and the third is in green. wP and oP represent to train on CIDNet with and without perceptual loss [36].
表 1: LOL (v1 和 v2) 数据集的定量比较 $\mathrm{PSNR/SSIM\uparrow}$。Normal 和 GT Mean 分别表示未经过和经过 Ground Truth 伽马校正的结果。最高结果标红,次高标青,第三标绿。wP 和 oP 表示 CIDNet 是否使用感知损失 [36] 进行训练。
| Methods | Params/M | FLOPs/G | LOLv1 Normal PSNR | SSIM | GT Mean PSNR | SSIM | LOLv2-Real Normal PSNR | SSIM | GT Mean PSNR | SSIM | LOLv2-Syn Normal PSNR | SSIM | GT Mean PSNR | SSIM |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RetinexNet[6] | 0.84 | 584.47 | 16.774 | 0.419 | 18.915 | 0.427 | 16.097 | 0.401 | 18.323 | 0.447 | 17.137 | 0.762 | 19.099 | 0.774 |
| KinD [2] | 8.02 | 34.99 | 17.650 | 0.775 | 20.860 | 0.802 | 14.740 | 0.641 | 17.544 | 0.669 | 13.290 | 0.578 | 16.259 | 0.591 |
| ZeroDCE [4] | 0.075 | 4.83 | 14.861 | 0.559 | 21.880 | 0.640 | 16.059 | 0.580 | 19.771 | 0.671 | 17.712 | 0.815 | 21.463 | 0.848 |
| 3DLUT [37] | 0.59 | 7.67 | 14.350 | 0.445 | 21.350 | 0.585 | 17.590 | 0.721 | 20.190 | 0.745 | 18.040 | 0.800 | 22.173 | 0.854 |
| DRBN [38] | 5.47 | 48.61 | 16.290 | 0.617 | 19.550 | 0.746 | 20.290 | 0.831 | - | - | 23.220 | 0.927 | - | - |
| RUAS [39] | 0.003 | 0.83 | 16.405 | 0.500 | 18.654 | 0.518 | 15.326 | 0.488 | 19.061 | 0.510 | 13.765 | 0.638 | 16.584 | 0.719 |
| LLFlow [5] | 17.42 | 358.4 | 21.149 | 0.854 | 24.998 | 0.871 | 17.433 | 0.831 | 25.421 | 0.877 | 24.807 | 0.919 | 27.961 | 0.930 |
| EnlightenGAN [3] | 114.35 | 61.01 | 17.480 | 0.651 | 20.003 | 0.691 | 18.230 | 0.617 | - | - | 16.570 | 0.734 | - | - |
| Restormer [40] | 26.13 | 144.25 | 22.365 | 0.816 | 26.682 | 0.853 | 18.693 | 0.834 | 26.116 | 0.853 | 21.413 | 0.830 | 25.428 | 0.859 |
| LEDNet [35] | 7.07 | 35.92 | 20.627 | 0.823 | 25.470 | 0.846 | 19.938 | 0.827 | 27.814 | 0.870 | 23.709 | 0.914 | 27.367 | 0.928 |
| SNR-Aware [15] | 4.01 | 26.35 | 24.610 | 0.842 | 26.716 | 0.851 | 21.480 | 0.849 | 27.209 | 0.871 | 24.140 | 0.928 | 27.787 | 0.941 |
| PairLIE [7] | 0.33 | 20.81 | 19.510 | 0.736 | 23.526 | 0.755 | 19.885 | 0.778 | 24.025 | 0.803 | - | - | - | - |
| LLFormer [41] | 24.55 | 22.52 | 23.649 | 0.816 | 25.758 | 0.823 | 20.056 | 0.792 | 26.197 | 0.819 | 24.038 | 0.909 | 28.006 | 0.927 |
| RetinexFormer [14] | 1.53 | 15.85 | 25.153 | 0.846 | 27.140 | 0.850 | 22.794 | 0.840 | 27.694 | 0.856 | 25.670 | 0.930 | 28.992 | 0.939 |
| CIDNet-wP | 1.88 | 7.57 | 23.809 | 0.857 | 27.715 | 0.876 | 24.111 | 0.868 | 28.134 | 0.892 | 25.129 | 0.939 | 29.367 | 0.950 |
| CIDNet-oP | 1.88 | 7.57 | 23.500 | 0.870 | 28.141 | 0.889 | 23.427 | 0.862 | 27.762 | 0.881 | 25.705 | 0.942 | 29.566 | 0.950 |

Fig. 6: Input Sony-Total-Dark extreme low-light image with the image enhanced by our CIDNet.

图 6: 输入Sony-Total-Dark极低光图像及经CIDNet增强后的效果。
LOL. The LOL dataset has v1 [6] and v2 [27] versions. LOL-v2 is divided into real and synthetic subsets. The training and testing sets are split in proportion to 485:15, 689:100, and 900:100 on LOL-v1, LOL-v2-Real, and LOL-v2-Synthetic. For LOLv1 and LOLv2-Real, we crop the training images into $400\times400$ patches and train CIDNet for 1500 epochs with a batch size of 8. For LOLv2-Synthetic, we set the batch size to 1 and trained 500 epochs without cropping.
LOL。LOL数据集包含v1 [6]和v2 [27]两个版本。LOL-v2分为真实和合成两个子集。训练集与测试集在LOL-v1、LOL-v2-Real和LOL-v2-Synthetic上的划分比例分别为485:15、689:100和900:100。对于LOLv1和LOLv2-Real,我们将训练图像裁剪为$400\times400$的块,以批量大小8训练CIDNet 1500轮次。对于LOLv2-Synthetic,我们设置批量大小为1,不进行裁剪并训练500轮次。
SICE. The original SICE dataset [32] contains a total of 589 sets of low-light and overexposed images, and the training set, validation set, and test set are divided into three groups according to 7:1:2. We train on the SICE training set with the batch size of 10 and test on the datasets SICE-Mix and SICEGrad [33]. We crop the original SICE image by $160\times160$ and train CIDNet over 1000 epochs.
SICE。原始SICE数据集[32]共包含589组低光和过曝图像,训练集、验证集和测试集按7:1:2的比例划分。我们在SICE训练集上以批次大小(batch size)为10进行训练,并在SICE-Mix和SICEGrad[33]数据集上测试。将原始SICE图像裁剪为$160\times160$尺寸,并对CIDNet进行1000轮(epoch)训练。
Sony-Total-Dark. This dataset is a customized version of the subset of SID dataset captured by the Sony $\alpha7\mathrm{{S}}$ II camera, which is adopted for evaluation. There are 2697 shortlong-exposure RAW image pairs. To make this dataset more challenging, we convert the RAW format images to sRGB images with no gamma correction as Fig. 6, which resulted in images becoming extremely dark. We crop the training images into $256\times256$ patches and train CIDNet for 1500 epochs with a batch size of 4.
Sony-Total-Dark。该数据集是SID数据集中由Sony $\alpha7\mathrm{{S}}$ II相机拍摄的子集定制版本,用于评估。包含2697组短长曝光RAW图像对。为提升挑战性,我们将RAW格式图像转换为未经伽马校正的sRGB图像(如图6所示),导致图像变得极暗。训练图像被裁剪为$256\times256$的块,以批量大小4训练CIDNet 1500轮次。
TABLE II: Quantitative comparisons $\mathrm{LPIPS/FLOPs\downarrow}$ on LOL (v1 and v2) datasets. GT Mean represents the gamma-corrected image by Ground Truth. The best result is in red color.
表 II: 定量比较 $\mathrm{LPIPS/FLOPs\downarrow}$ 在 LOL (v1 和 v2) 数据集上的表现。GT Mean 表示 Ground Truth 的伽马校正图像。最佳结果以红色标注。
| 方法 | LOLv1 | LOLv2-Real | LOLv2-Syn | 复杂度 FLOPs/G↓ | |||
|---|---|---|---|---|---|---|---|
| Normal | GT Mean | Normal | GT Mean | Normal | GT Mean | ||
| EnlightenGAN | 0.322 | 0.317 | 0.309 | 0.301 | 0.220 | 0.213 | 61.01 |
| RetinexNet | 0.474 | 0.470 | 0.543 | 0.519 | 0.255 | 0.247 | 587.47 |
| LLFormer | 0.1 |
