Π nets: Deep Polynomial Neural Networks

Π网络：深度多项式神经网络

Abstract

摘要

Deep Convolutional Neural Networks (DCNNs) is currently the method of choice both for generative, as well as for disc rim i native learning in computer vision and machine learning. The success of DCNNs can be attributed to the careful selection of their building blocks (e.g., residual blocks, rectifiers, sophisticated normalization schemes, to mention but a few). In this paper, we propose Π-Nets, a new class of DCNNs. Π-Nets are polynomial neural networks, i.e., the output is a high-order polynomial of the input. Π- Nets can be implemented using special kind of skip connections and their parameters can be represented via high-order tensors. We empirically demonstrate that Π-Nets have better representation power than standard DCNNs and they even produce good results without the use of non-linear activation functions in a large battery of tasks and signals, i.e., images, graphs, and audio. When used in conjunction with activation functions, Π-Nets produce state-of-the-art results in challenging tasks, such as image generation. Lastly, our framework elucidates why recent generative models, such as StyleGAN, improve upon their predecessors, e.g., ProGAN.

深度卷积神经网络 (DCNNs) 是目前计算机视觉和机器学习中生成式与判别式学习的首选方法。DCNNs 的成功可归因于对其构建模块的精心选择 (例如残差块、整流器、复杂的归一化方案等)。本文提出了一类新型 DCNNs——Π-Nets，这是一种多项式神经网络，其输出是输入的高阶多项式。Π-Nets 可通过特殊类型的跳跃连接实现，其参数可用高阶张量表示。我们通过实验证明，在图像、图和音频等多种任务和信号中，Π-Nets 比标准 DCNNs 具有更强的表征能力，甚至在不使用非线性激活函数的情况下也能取得良好效果。当与激活函数结合使用时，Π-Nets 在图像生成等挑战性任务中达到了最先进的水平。最后，我们的框架阐明了 StyleGAN 等近期生成模型为何能超越 ProGAN 等前代模型。

1. Introduction

1. 引言

Representation learning via the use of (deep) multilayered non-linear models has revolutionised the field of computer vision the past decade [32, 17]. Deep Convolutional Neural Networks (DCNNs) [33, 32] have been the dominant class of models. Typically, a DCNN is a sequence of layers where the output of each layer is fed first to a convolutional operator (i.e., a set of shared weights applied via the convolution operator) and then to a non-linear activation function. Skip connections between various layers allow deeper representations and improve the gradient flow while training the network [17, 54].

通过使用(深度)多层非线性模型进行表征学习，在过去十年彻底改变了计算机视觉领域[32,17]。深度卷积神经网络(DCNNs)[33,32]一直是主导模型类别。通常，DCNN是由一系列层级组成的结构，每层的输出先经过卷积算子(即通过卷积运算应用的一组共享权重)，再通过非线性激活函数处理。不同层级间的跳跃连接(skip connections)可以实现更深层级的表征，并改善网络训练时的梯度流动[17,54]。

In the aforementioned case, if the non-linear activation functions are removed, the output of a DCNN degenerates to a linear function of the input. In this paper, we propose a new class of DCNNs, which we coin Π´nets, where the output is a polynomial function of the input. We design Π´nets for generative tasks (e.g., where the input is a small dimensional noise vector) as well as for disc rim i native tasks (e.g., where the input is an image and the output is a vector with dimensions equal to the number of labels). We demonstrate that these networks can produce good results without the use of non-linear activation functions. Furthermore, our extensive experiments show, empirically, that Π´nets can consistently improve the performance, in both generative and disc rim i native tasks, using, in many cases, significantly fewer parameters.

在上述情况下，如果移除非线性激活函数，DCNN的输出会退化为输入的线性函数。本文提出了一类新型DCNN，称为Π´net，其输出是输入的多项式函数。我们为生成式任务(例如输入为低维噪声向量)和判别式任务(例如输入为图像且输出为维度等于标签数量的向量)设计了Π´net。实验证明，这些网络无需使用非线性激活函数即可产生良好结果。此外，大量实验表明，Π´net在生成式和判别式任务中均能持续提升性能，且多数情况下参数量显著减少。

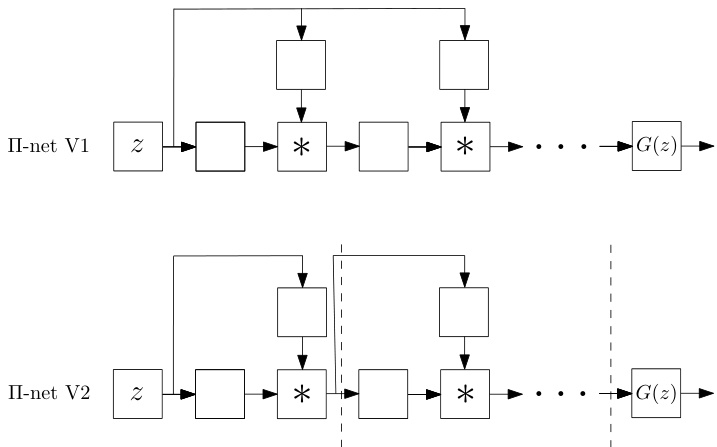
Figure 1: In this paper we introduce a class of networks called $\Pi-$ nets, where the output is a polynomial of the input. The input in this case, $_{z}$ , can be either the latent space of Generative Adversarial Network for a generative task or an image in the case of a discriminative task. Our polynomial networks can be easily implemented using a special kind of skip connections.

图 1: 本文介绍了一类称为$\Pi-$网络的结构，其输出是输入的多项式。此处的输入$_{z}$可以是生成式对抗网络(Generative Adversarial Network)在生成任务中的隐空间，也可以是判别任务中的图像。我们的多项式网络可通过一种特殊的跳跃连接(skip connections)轻松实现。

DCNNs have been used in computer vision for over 30 years [33, 50]. Arguably, what brought DCNNs again in mainstream research was the remarkable results achieved by the so-called AlexNet in the ImageNet challenge [32]. Even though it is only seven years from this pioneering effort the field has witnessed dramatic improvement in all datadependent tasks, such as object detection [21] and image generation [37, 15], just to name a few examples. The improvement is mainly attributed to carefully selected units in the architectural pipeline of DCNNs, such as blocks with skip connections [17], sophisticated normalization schemes (e.g., batch normalisation [23]), as well as the use of efficient gradient-based optimization techniques [28].

深度卷积神经网络 (DCNNs) 在计算机视觉领域已有超过 30 年的应用历史 [33, 50]。可以说，让 DCNNs 重新成为主流研究的契机是 AlexNet 在 ImageNet 挑战赛中取得的突破性成果 [32]。尽管距离这一开创性工作仅过去七年，该领域已在所有依赖数据的任务中取得了显著进步，例如目标检测 [21] 和图像生成 [37, 15] 等。这些进步主要归功于对 DCNN 架构流程中组件的精心选择，例如带有跳跃连接 (skip connections) 的模块 [17]、复杂的归一化方案（如批量归一化 [23]），以及高效梯度优化技术 [28] 的应用。

Parallel to the development of DCNN architectures for disc rim i native tasks, such as classification, the notion of Generative Adversarial Networks (GANs) was introduced for training generative models. GANs became instantly a popular line of research but it was only after the careful design of DCNN pipelines and training strategies that GANs were able to produce realistic images [26, 2]. ProGAN [25] was the first architecture to synthesize realistic facial images by a DCNN. StyleGAN [26] is a follow-up work that improved ProGAN. The main addition of StyleGAN was a type of skip connections, called ADAIN [22], which allowed the latent representation to be infused in all different layers of the generator. Similar infusions were introduced in [42] for conditional image generation.

在开发用于分类等判别任务的DCNN架构的同时，生成对抗网络（GAN）的概念被提出用于训练生成模型。GAN迅速成为热门研究方向，但只有在精心设计DCNN流程和训练策略后，GAN才能生成逼真图像[26, 2]。ProGAN[25]是首个通过DCNN合成逼真人脸图像的架构。StyleGAN[26]作为后续研究改进了ProGAN，其主要创新是一种称为ADAIN[22]的跳跃连接，允许潜在表征注入生成器的所有不同层。文献[42]针对条件图像生成提出了类似的注入机制。

Our work is motivated by the improvement of StyleGAN over ProGAN by such a simple infusion layer and the need to provide an explanation 1. We show that such infusion layers create a special non-linear structure, i.e., a higher-order polynomial, which empirically improves the representation power of DCNNs. We show that this infusion layer can be generalized (e.g. see Fig. 1) and applied in various ways in both generative, as well as disc rim i native architectures. In particular, the paper bears the following contributions:

我们的研究灵感源于StyleGAN通过简单注入层对ProGAN的改进以及解释需求[1]。我们证明这类注入层会形成特殊的非线性结构（即高阶多项式），实验表明其能提升深度卷积神经网络(DCNNs)的表征能力。如图1所示，这种注入层具有可泛化性，可灵活应用于生成式与判别式架构。本文具体贡献包括：

• We propose a new family of neural networks (called Π´nets) where the output is a high-order polynomial of the input. To avoid the combinatorial explosion in the number of parameters of polynomial activation functions [27] our Π´nets use a special kind of skip connections to implement the polynomial expansion (please see Fig. 1 for a brief schematic representation). We theoretically demonstrate that these kind of skip connections relate to special forms of tensor decompositions. • We show how the proposed architectures can be applied in generative models such as GANs, as well as disc rim i native networks. We showcase that the resulting architectures can be used to learn high-dimensional distributions without non-linear activation functions. • We convert state-of-the-art baselines using the proposed

• 我们提出了一种新型神经网络家族(称为Π´nets)，其输出是输入的高阶多项式。为避免多项式激活函数参数数量的组合爆炸[27]，我们的Π´nets采用特殊跳跃连接来实现多项式展开(简要示意图见图1)。我们从理论上证明这类跳跃连接与特定形式的张量分解相关。
• 我们展示了所提架构如何应用于生成式模型(如GAN)和判别式网络。实验证明该架构无需非线性激活函数即可学习高维分布。
• 我们将现有先进基线模型转换为...

Π´nets and show how they can largely improve the expressivity of the baseline. We demonstrate it conclusively in a battery of tasks (i.e., generation and classification). Finally, we demonstrate that our architectures are applicable to many different signals such as images, meshes, and audio.

Π´nets 并展示它们如何大幅提升基线的表达能力。我们通过一系列任务（即生成和分类）进行了充分验证。最后，我们证明了该架构可适用于图像、网格和音频等多种信号。

2. Related work

2. 相关工作

Expressivity of (deep) neural networks: The last few years, (deep) neural networks have been applied to a wide range of applications with impressive results. The performance boost can be attributed to a host of factors including: a) the availability of massive datasets [4, 35], b) the machine learning libraries [57, 43] running on massively parallel hardware, c) training improvements. The training improvements include a) optimizer improvement [28, 46], b) augmented capacity of the network [53], c) regular iz ation tricks [11, 49, 23, 58]. However, the paradigm for each layer remains largely unchanged for several decades: each layer is composed of a linear transformation and an element-wise activation function. Despite the variety of linear transformations [9, 33, 32] and activation functions [44, 39] being used, the effort to extend this paradigm has not drawn much attention to date.

(深度)神经网络的表达能力：过去几年，(深度)神经网络已在众多领域展现出惊人性能。这种提升可归因于以下因素：a) 海量数据集[4,35]的可用性；b) 基于大规模并行硬件的机器学习库[57,43]；c) 训练优化技术。训练优化具体包括：a) 优化器改进[28,46]；b) 网络容量增强[53]；c) 正则化技巧[11,49,23,58]。但数十年来，每层网络的底层范式基本未变：均由线性变换和逐元素激活函数构成。尽管存在多种线性变换[9,33,32]和激活函数[44,39]方案，突破该范式的尝试至今仍未引起足够重视。

Recently, hierarchical models have exhibited stellar performance in learning expressive generative models [2, 26, 70]. For instance, the recent BigGAN [2] performs a hierarchical composition through skip connections from the noise $_{z}$ to multiple resolutions of the generator. A similar idea emerged in StyleGAN [26], which is an improvement over the Progressive Growing of GANs (ProGAN) [25]. As ProGAN, StyleGAN is a highly-engineered network that achieves compelling results on synthesized 2D images. In order to provide an explanation on the improvements of StyleGAN over ProGAN, the authors adopt arguments from the style transfer literature [22]. We believe that these improvements can be better explained under the light of our proposed polynomial function approximation. Despite the hierarchical composition proposed in these works, we present an intuitive and mathematically elaborate method to achieve a more precise approximation with a polynomial expansion. We also demonstrate that such a polynomial expansion can be used in both image generation (as in [26, 2]), image classification, and graph representation learning.

最近，分层模型在学习表达性生成模型方面展现出卓越性能[2, 26, 70]。例如，最新的BigGAN[2]通过从噪声$_{z}$到生成器多分辨率的跳跃连接实现分层组合。类似思想出现在StyleGAN[26]中，这是对渐进增长GAN(ProGAN)[25]的改进。与ProGAN一样，StyleGAN是经过高度工程化的网络，在合成2D图像上取得了令人信服的结果。为了解释StyleGAN相对ProGAN的改进，作者采用了风格迁移文献[22]中的论点。我们认为这些改进可以通过我们提出的多项式函数近似得到更好解释。尽管这些工作提出了分层组合方法，但我们提出了一种直观且数学严谨的多项式展开方法来实现更精确的近似。我们还证明这种多项式展开可同时应用于图像生成(如[26, 2])、图像分类和图表示学习。

Polynomial networks: Polynomial relationships have been investigated in two specific categories of networks: a) self-organizing networks with hard-coded feature selection, b) pi-sigma networks.

多项式网络：多项式关系已在两类特定网络中被研究：a) 具有硬编码特征选择的自组织网络，b) Pi-Sigma网络。

The idea of learnable polynomial features can be traced back to Group Method of Data Handling (GMDH) $[24]^{2}$ . GMDH learns partial descriptors that capture quadratic correlations between two predefined input elements. In [41], more input elements are allowed, while higher-order polynomials are used. The input to each partial descriptor is predefined (subset of the input elements), which does not allow the method to scale to high-dimensional data with complex correlations.

可学习多项式特征的思想可以追溯到数据处理分组方法 (GMDH) [24]^2。GMDH通过学习部分描述符来捕捉两个预定义输入元素之间的二次相关性。在[41]中，该方法允许更多输入元素，同时使用更高阶多项式。每个部分描述符的输入都是预定义的（输入元素的子集），这使得该方法无法扩展到具有复杂相关性的高维数据。

Shin et al. [51] introduce the pi-sigma network, which is a neural network with a single hidden layer. Multiple affine transformations of the data are learned; a product unit multiplies all the features to obtain the output. Improvements in the pi-sigma network include regular iz ation for training in [66] or using multiple product units to obtain the output in [61]. The pi-sigma network is extended in sigma-pi-sigma neural network (SPSNN) [34]. The idea of SPSNN relies on summing different pi-sigma networks to obtain each output. SPSNN also uses a predefined basis (overlapping rectangular pulses) on each pi-sigma sub-network to filter the input features. Even though such networks use polynomial features or products, they do not scale well in high-dimensional signals. In addition, their experimental evaluation is conducted only on signals with known ground-truth distributions (and with up to 3 dimensional input/output), unlike the modern generative models where only a finite number of samples from high-dimensional ground-truth distributions is available.

Shin等人[51]提出了pi-sigma网络，这是一种具有单隐藏层的神经网络。该网络学习数据的多重仿射变换，通过乘积单元将所有特征相乘获得输出。针对pi-sigma网络的改进包括文献[66]提出的训练正则化方法，以及文献[61]采用多重乘积单元获取输出的方案。该网络在sigma-pi-sigma神经网络(SPSNN)[34]中得到扩展，其核心思想是通过叠加不同pi-sigma网络来获得每个输出。SPSNN还在每个pi-sigma子网络中使用预定义基函数（重叠矩形脉冲）来过滤输入特征。尽管这类网络采用了多项式特征或乘积运算，但在高维信号中扩展性不佳。此外，其实验评估仅针对已知真实分布的信号（且输入/输出维度不超过3维），这与现代生成模型形成对比——后者仅需从高维真实分布中获取有限样本即可工作。

3. Method

3. 方法

Notation: Tensors are symbolized by calligraphic letters, e.g., ${x}$ , while matrices (vectors) are denoted by uppercase (lowercase) boldface letters e.g., $\ensuremath{\boldsymbol{X}},(\ensuremath{\boldsymbol{x}})$ . The mode-m vector product of ${x}$ with a vector $\pmb{u}\in\mathbb{R}^{I_{m}}$ is denoted by $\pmb{x}\times_{m}\pmb{u}$ .3

符号说明：张量 (tensor) 用花体字母表示，例如 ${x}$，矩阵 (matrix) 用大写粗体字母表示 (如 $\ensuremath{\boldsymbol{X}}$)，向量 (vector) 用小写粗体字母表示 (如 $\ensuremath{\boldsymbol{x}}$)。张量 ${x}$ 与向量 $\pmb{u}\in\mathbb{R}^{I_{m}}$ 的模-m向量积记为 $\pmb{x}\times_{m}\pmb{u}$。

We want to learn a function approx im at or where each element of the output $x_{j}$ , with $j\in[1,o]$ , is expressed as a polynomial 4 of all the input elements $z_{i}$ , with $i\in[1,d]$ . That is, we want to learn a function $G:\mathbb{R}^{d}\rightarrow\mathbb{R}^{o}$ of order $N\in\mathbb N$ , such that:

我们想要学习一个函数近似器，其中输出的每个元素 $x_{j}$（$j\in[1,o]$）表示为所有输入元素 $z_{i}$（$i\in[1,d]$）的多项式。也就是说，我们希望学习一个阶数为 $N\in\mathbb N$ 的函数 $G:\mathbb{R}^{d}\rightarrow\mathbb{R}^{o}$，满足：

$$
\begin{array}{r}{x_{j}=G(z){j}=\beta_{j}+\pmb{w}{j}^{[1]^{T}}z+z^{T}\pmb{W}{j}^{[2]}z+}\ {\pmb{w}{j}^{[3]}\times_{1}z\times_{2}z\times_{3}z+\cdot\cdot..+\pmb{\mathscr{W}}{j}^{[N]}\displaystyle\prod_{n=1}^{N}\times_{n}z}\end{array}
$$

$$
\begin{array}{r}{x_{j}=G(z){j}=\beta_{j}+\pmb{w}{j}^{[1]^{T}}z+z^{T}\pmb{W}{j}^{[2]}z+}\ {\pmb{w}{j}^{[3]}\times_{1}z\times_{2}z\times_{3}z+\cdot\cdot..+\pmb{\mathscr{W}}{j}^{[N]}\displaystyle\prod_{n=1}^{N}\times_{n}z}\end{array}
$$

where βj P R, and Wrjns P Rśnm“1 ˆmd N are parameters for approximating the output $x_{j}$ . The correlations (of the input elements $z_{i}$ ) up to $N^{t{\bar{h}}}$ order emerge in (1). A more compact expression of (1) is obtained by vector i zing the outputs:

其中βj ∈ R，Wrjns ∈ Rśnm“1 ˆmd N 是用于逼近输出$x_{j}$的参数。(1)式中出现了输入元素$z_{i}$最高至$N^{t{\bar{h}}}$阶的相关性。通过向量化输出可以得到(1)式更简洁的表达式：

$$
\pmb{x}=G(z)=\sum_{n=1}^{N}\left(\pmb{\mathcal{W}}^{[n]}\prod_{j=2}^{n+1}\times_{j}z\right)+\beta
$$

$$
\pmb{x}=G(z)=\sum_{n=1}^{N}\left(\pmb{\mathcal{W}}^{[n]}\prod_{j=2}^{n+1}\times_{j}z\right)+\beta
$$

where β P Ro and Wrns P Roˆśnm“1 ˆmd N are the learnable parameters. This form of (2) allows us to approximate any smooth function (for large $N$ ), however the parameters grow with $\mathcal{O}(d^{N})$ .

其中β ∈ ℝ^o和W_rns ∈ ℝ^{o×∏_{m=1}^N d_m}是可学习参数。这种形式的(2)允许我们逼近任何光滑函数(对于较大的$N$)，但参数会以$\mathcal{O}(d^{N})$的复杂度增长。

A variety of methods, such as pruning [8, 16], tensor decomposition s [29, 52], special linear operators [6] with reduced parameters, parameter sharing/prediction [67, 5], can be employed to reduce the parameters. In contrast to the heuristic approaches of pruning or prediction, we describe below two principled ways which allow an efficient implementation. The first method relies on performing an off-the-shelf tensor decomposition on (2), while the second considers the final polynomial as the product of lower-degree polynomials.

可以采用多种方法来减少参数，例如剪枝 [8, 16]、张量分解 [29, 52]、参数减少的特殊线性算子 [6]、参数共享/预测 [67, 5]。与剪枝或预测的启发式方法不同，我们下面描述两种允许高效实现的原则性方法。第一种方法依赖于对(2)执行现成的张量分解，而第二种方法将最终多项式视为低次多项式的乘积。

The tensor decomposition s are used in this paper to provide a theoretical understanding (i.e., what is the order of the polynomial used) of the proposed family of Π-nets. Implementation-wise the incorporation of different $\Pi$ -net structures is as simple as the in corpora t ation of a skipconnection. Nevertheless, in $\Pi$ -net different skip connections lead to different kinds of polynomial networks.

本文使用张量分解 (tensor decomposition) 为提出的Π网络家族提供理论解释 (即所用多项式的阶数)。在实现层面，集成不同$\Pi$网络结构的操作如同添加跳跃连接 (skip connection) 一样简单。然而在$\Pi$网络中，不同的跳跃连接会生成不同类型的多项式网络。

3.1. Single polynomial

3.1. 单多项式

A tensor decomposition on the parameters is a natural way to reduce the parameters and to implement (2) with a neural network. Below, we demonstrate how three such decomposition s result in novel architectures for a neural network training. The main symbols are summarized in Table 1, while the equivalence between the recursive relationship and the polynomial is analyzed in the supplementary.

对参数进行张量分解是减少参数并用神经网络实现(2)的自然方法。下面我们将展示三种此类分解如何产生新颖的神经网络训练架构。主要符号汇总在表1中，而递归关系与多项式之间的等价性分析详见补充材料。

Model 1: CCP: A coupled CP decomposition [29] is applied on the parameter tensors. That is, each parameter tensor, i.e. $w^{[\dot{n}]}$ for $n\in[1,N]$ , is not factorized individually, but rather a coupled factorization of the parameters is defined. The recursive relationship is:

模型1: CCP: 对参数张量采用耦合CP分解[29]。即每个参数张量(如$w^{[\dot{n}]}$, $n\in[1,N]$)不再单独分解，而是定义参数的耦合分解。其递推关系为:

$$
\pmb{x}{n}=\left(U_{[n]}^{T}z\right)\ast\pmb{x}{n-1}+\pmb{x}_{n-1}
$$

$$
\pmb{x}{n}=\left(U_{[n]}^{T}z\right)\ast\pmb{x}{n-1}+\pmb{x}_{n-1}
$$

for $n=2,\ldots,N$ with $x_{1}=U_{[1]}^{T}z$ and ${\pmb x}={\pmb C}{\pmb x}{N}+\beta$ The parameters $C\in\mathbb{R}^{o\times k},\pmb{U}_{[n]}\bar{\in\mathbb{R}}^{d\times k}$ for $n=1,\ldots,N$ are learnable. To avoid overloading the diagram, a schematic assuming a third order expansion $N=3,$ ) is illustrated in Fig. 2.

对于 $n=2,\ldots,N$，其中 $x_{1}=U_{[1]}^{T}z$ 且 ${\pmb x}={\pmb C}{\pmb x}{N}+\beta$。参数 $C\in\mathbb{R}^{o\times k},\pmb{U}_{[n]}\bar{\in\mathbb{R}}^{d\times k}$（$n=1,\ldots,N$）是可学习的。为避免图示过载，图 2 展示了三阶展开 $N=3$ 的示意图。

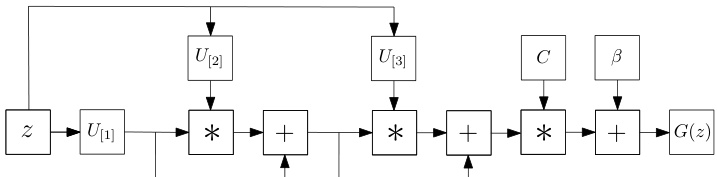
Figure 2: Schematic illustration of the CCP (for third order approximation). Symbol $^*$ refers to the Hadamard product.

图 2: CCP(三阶近似)示意图。符号 $^*$ 表示哈达玛积(Hadamard product)。

Model 2: NCP: Instead of defining a flat CP decomposition, we can utilize a joint hierarchical decomposition on the polynomial parameters. A nested coupled CP decomposition (NCP), which results in the following recursive relationship for $N^{t h}$ order approximation is defined:

模型2：NCP：不同于定义平坦的CP分解，我们可以对多项式参数采用联合层次分解。嵌套耦合CP分解（NCP）由此产生，其第N阶近似遵循以下递归关系：

Table 1: Nomenclature

表 1: 术语表

符号	维度	定义
n, N k 之	N N Rd	多项式项阶数、总逼近阶数。分解的秩。多项式逼近器(即生成器)的输入。

$$
\pmb{x}{n}=\left(\pmb{A}{[n]}^{T}\pmb{z}\right)*\left(\pmb{S}{[n]}^{T}\pmb{x}{n-1}+\pmb{B}{[n]}^{T}\pmb{b}_{[n]}\right)
$$

$$
\pmb{x}{n}=\left(\pmb{A}{[n]}^{T}\pmb{z}\right)*\left(\pmb{S}{[n]}^{T}\pmb{x}{n-1}+\pmb{B}{[n]}^{T}\pmb{b}_{[n]}\right)
$$

for $n=2,\ldots,N$ with $\pmb{x}{1}=\left({\pmb A}{[n]}^{T}{\pmb z}\right)*\left({\pmb B}{[n]}^{T}{\pmb b}{[n]}\right)$ and ${\pmb x}={\pmb C}{\pmb x}{N}+\beta$ . The parameters $C\in\mathbb{R}^{o\times k},A_{[n]}\in$ $\mathbb{R}^{d\times k},S_{[n]}\in\mathbb{R}^{k\times k},B_{[n]}\in\mathbb{R}^{\omega\times k}$ , $b_{[n]} \in~\mathbb{R}^{\omega}$ for $n=$ $1,\ldots,N$ , are learnable. The explanation of each variable is elaborated in the supplementary, where the decomposition is derived.

对于 $n=2,\ldots,N$，其中 $\pmb{x}{1}=\left({\pmb A}{[n]}^{T}{\pmb z}\right)*\left({\pmb B}{[n]}^{T}{\pmb b}{[n]}\right)$ 且 ${\pmb x}={\pmb C}{\pmb x}{N}+\beta$。参数 $C\in\mathbb{R}^{o\times k},A_{[n]}\in$ $\mathbb{R}^{d\times k},S_{[n]}\in\mathbb{R}^{k\times k},B_{[n]}\in\mathbb{R}^{\omega\times k}$，$b_{[n]}\in~\mathbb{R}^{\omega}$ 对于 $n=$ $1,\ldots,N$ 是可学习的。各变量的详细解释及分解推导见补充材料。

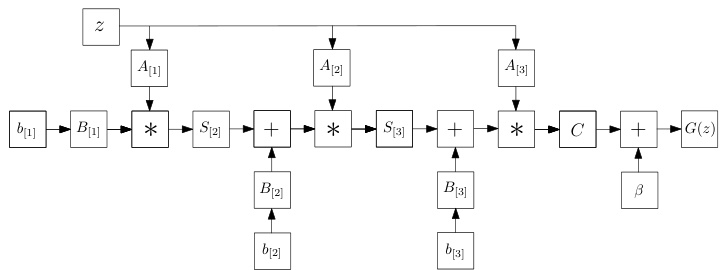
Figure 3: Schematic illustration of the NCP (for third order approximation). Symbol $^*$ refers to the Hadamard product.

图 3: NCP (三阶近似) 示意图。符号 $^*$ 表示 Hadamard 积。

Model 3: NCP-Skip: The expressiveness of NCP can be further extended using a skip connection (motivated by CCP). The new model uses a nested coupled decomposition and has the following recursive expression:

模型 3: NCP-Skip: 通过引入跳跃连接 (受CCP启发) 可进一步扩展NCP的表达能力。该新模型采用嵌套耦合分解，其递归表达式如下:

$$
\pmb{x}{n}=\left(\pmb{A}{[n]}^{T}\pmb{z}\right)\ast\left(\pmb{S}{[n]}^{T}\pmb{x}{n-1}+\pmb{B}{[n]}^{T}\pmb{b}{[n]}\right)+\pmb{x}_{n-1}
$$

$$
\pmb{x}{n}=\left(\pmb{A}{[n]}^{T}\pmb{z}\right)\ast\left(\pmb{S}{[n]}^{T}\pmb{x}{n-1}+\pmb{B}{[n]}^{T}\pmb{b}{[n]}\right)+\pmb{x}_{n-1}
$$

for $n=2,\ldots,N$ with $\pmb{x}{1}=\left(\pmb{A}{[n]}^{T}\pmb{z}\right)\ast\left(\pmb{B}{[n]}^{T}\pmb{b}{[n]}\right)$ and ${\pmb x}={\pmb C}{\pmb x}_{N}+\beta$ . The learnable parameters are the same as in NCP, however the difference in the recursive form results in a different polynomial expansion and thus architecture.

对于 $n=2,\ldots,N$，其中 $\pmb{x}{1}=\left(\pmb{A}{[n]}^{T}\pmb{z}\right)\ast\left(\pmb{B}{[n]}^{T}\pmb{b}{[n]}\right)$ 且 ${\pmb x}={\pmb C}{\pmb x}_{N}+\beta$。可学习参数与NCP相同，但递归形式的不同导致了多项式展开的差异，从而形成了不同的架构。

Comparison between the models: All three models are based on a polynomial expansion, however their recursive forms and employed decomposition s differ. The CCP has a simpler expression, however the NCP and the NCP-Skip relate to standard architectures using hierarchical composition that have recently yielded promising results in both generative and disc rim i native tasks. In the remainder of the paper, for comparison purposes we use the NCP by default for the image generation and NCP-Skip for the image classification. In our preliminary experiments, CCP and NCP share a similar performance based on the setting of Sec. 4. In all cases, to mitigate stability issues that might emerge during training, we employ certain normalization schemes that constrain the magnitude of the gradients. An in-depth theoretical analysis of the architectures is deferred to a future version of our work.

模型对比：
这三种模型均基于多项式展开，但它们的递归形式与所采用的分解方法各不相同。CCP表达式较为简洁，而NCP和NCP-Skip则关联到采用分层组合的标准架构，这些架构近期在生成式和判别式任务中均展现出良好效果。本文后续部分默认使用NCP进行图像生成实验，NCP-Skip用于图像分类实验以便对比。初步实验中，CCP与NCP在第四节设定下表现相近。所有实验均采用特定归一化方案约束梯度幅度，以缓解训练中可能出现的稳定性问题。架构的深度理论分析将留待后续工作版本探讨。

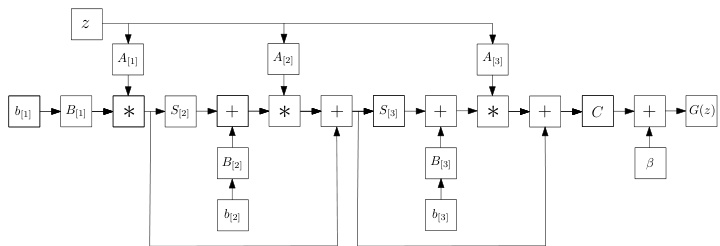
Figure 4: Schematic illustration of the NCP-Skip (for third order approximation). The difference from Fig. 3 is the skip connections added in this model.

图 4: NCP-Skip示意图(三阶近似)。与图3的区别在于该模型增加了跳跃连接。

3.2. Product of polynomials

3.2. 多项式乘积

Instead of using a single polynomial, we express the function approximation as a product of polynomials. The product is implemented as successive polynomials where the output of the $i^{t h}$ polynomial is used as the input for the $(i+1)^{t h}$ polynomial. The concept is visually depicted in Fig. 5; each polynomial expresses a second order expansion. Stacking $N$ such polynomials results in an overall order of $2^{N}$ . Trivially, if the approximation of each polynomial is $B$ and we stack $N$ such polynomials, the total order is $B^{N}$ . The product does not necessarily demand the same order in each polynomial, the expressivity and the expansion order of each polynomial can be different and dependent on the task, e.g. for generative tasks that the resolution increases progressively, the expansion order could increase in the last polynomials. In all cases, the final order will be the product of each polynomial.

我们不使用单一多项式，而是将函数近似表示为多项式的乘积。该乘积通过连续多项式实现，其中第$i^{t h}$个多项式的输出作为第$(i+1)^{t h}$个多项式的输入。这一概念在图5中直观展示：每个多项式表示二阶展开。堆叠$N$个这样的多项式将获得$2^{N}$阶的整体展开度。显然，若每个多项式的近似阶数为$B$且堆叠$N$个多项式，则总阶数为$B^{N}$。乘积中的多项式不必具有相同阶数，每个多项式的表达能力和展开阶数可因任务而异，例如在分辨率逐步提升的生成式任务中，最后几个多项式的展开阶数可递增。所有情况下，最终阶数均为各多项式阶数的乘积。

There are two main benefits of the product over the single polynomial: a) it allows using different decomposition s (e.g. like in Sec. 3.1) and expressive power for each polynomial; b) it requires much less parameters for achieving the same order of approximation. Given the benefits of the product of polynomials, we assume below that a product of polynomials is used, unless explicitly mentioned otherwise. The respective model of product polynomials is called ProdPoly.

该产品相较于单一多项式主要有两大优势：
a) 允许为每个多项式采用不同的分解方式（如第3.1节所述）和表达能力；
b) 在达到相同逼近阶数时所需参数大幅减少。鉴于多项式乘积的优越性，下文默认采用多项式乘积模型（除非另有说明），该模型称为ProdPoly。

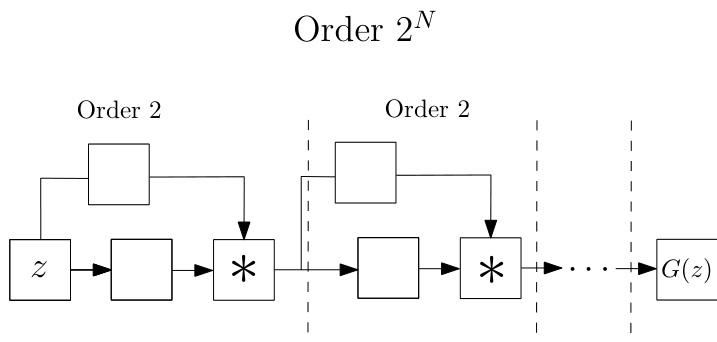
Figure 5: Abstract illustration of the ProdPoly. The input variable $_{z}$ on the left is the input to a $2^{n d}$ order expansion; the output of this is used as the input for the next polynomial (also with a $2^{n d}$ order expansion) and so on. If we use $N$ such polynomials, the final output $G(z)$ expresses a $2^{N}$ order expansion. In addition to the high order of approximation, the benefit of using the product of polynomials is that the model is flexible, in the sense that each polynomial can be implemented as a different decomposition of Sec. 3.1.

图 5: ProdPoly的抽象示意图。左侧输入变量 $_{z}$ 作为 $2^{n d}$ 阶展开的输入；其输出又作为下一个多项式(同样采用 $2^{n d}$ 阶展开)的输入，依此类推。若使用 $N$ 个这样的多项式，最终输出 $G(z)$ 将呈现 $2^{N}$ 阶展开。除了高阶近似能力外，采用多项式乘积的优势在于模型具有灵活性——每个多项式均可实现为第3.1节所述的不同分解形式。

3.3. Task-dependent input/output

3.3. 任务相关的输入/输出

The aforementioned polynomials are a function $\textbf{{x}}=$ $G(z)$ , where the input/output are task-dependent. For a generative task, e.g. learning a decoder, the input ${z}$ is typically some low-dimensional noise, while the output is a high-dimensional signal, e.g. an image. For a disc rim i native task the input ${z}$ is an image; for a domain adaptation task the signal ${z}$ denotes the source domain and $_{x}$ the target domain.

上述多项式是函数 $\textbf{{x}}=$ $G(z)$，其输入/输出取决于具体任务。对于生成式任务（例如学习解码器），输入 ${z}$ 通常是低维噪声，而输出是高维信号（如图像）。对于判别任务，输入 ${z}$ 是图像；对于域适应任务，信号 ${z}$ 表示源域，而 $_{x}$ 表示目标域。

4. Proof of concept

4. 概念验证

In this Section, we conduct motivational experiments in both generative and disc rim i native tasks to demonstrate the expressivity of Π´nets. Specifically, the networks are implemented without activation functions, i.e. only linear operations (e.g. convolutions) and Hadamard products are used. In this setting, the output is linear or multi-linear with respect to the parameters.

在本节中，我们在生成式和判别式任务中进行了动机实验，以证明Π´nets的表达能力。具体而言，这些网络在没有激活函数的情况下实现，即仅使用线性操作（如卷积）和Hadamard积。在此设置下，输出相对于参数是线性或多线性的。

4.1. Linear generation

4.1. 线性生成

One of the most popular generative models is Generative Adversarial Nets (GAN) [12]. We design a GAN, where the generator is implemented as a product of polynomials (using the NCP decomposition), while the disc rim in at or of [37] is used. No activation functions are used in the generator, but a single hyperbolic tangent (tanh) in the image space 5.

最流行的生成模型之一是生成对抗网络 (GAN) [12]。我们设计了一个GAN，其中生成器实现为多项式乘积 (使用NCP分解)，而判别器采用[37]的方案。生成器中没有使用激活函数，但在图像空间5中使用了单个双曲正切 (tanh)。

Figure 6: Linear interpolation in the latent space of ProdPoly (when trained on fashion images [64]). Note that the generator does not include any activation functions in between the linear blocks (Sec. 4.1). All the images are synthesized; the image on the leftmost column is the source, while the one in the rightmost is the target synthesized image.

图 6: ProdPoly (在时尚图像 [64] 上训练时) 潜在空间中的线性插值。注意生成器在线性块之间不包含任何激活函数 (第 4.1 节)。所有图像均为合成图像；最左侧列图像为源图像，最右侧列图像为目标合成图像。

Figure 7: Linear interpolation in the latent space of ProdPoly (when trained on facial images [10]). As in Fig. 6, the generator includes only linear blocks; the image on the leftmost column is the source, while the one in the rightmost is the target image.

图 7: ProdPoly 潜在空间中的线性插值 (在面部图像上训练时 [10])。与图 6 相同，生成器仅包含线性块；最左侧列中的图像是源图像，而最右侧列中的是目标图像。

Two experiments are conducted with a polynomial generator (Fashion-Mnist and YaleB). We perform a linear inter pol ation in the latent space when trained with FashionMnist [64] and with YaleB [10] and visualize the results in Figs. 6, 7, respectively. Note that the linear interpolation generates plausible images and navigates among different categories, e.g. trousers to sneakers or trousers to t-shirts. Equivalently, it can linearly traverse the latent space from a fully illuminated to a partly dark face.

我们使用多项式生成器进行了两项实验（Fashion