COTR: Correspondence Transformer for Matching Across Images

COTR: 跨图像匹配的对应关系Transformer

Abstract

摘要

We propose a novel framework for finding correspond ences in images based on a deep neural network that, given two images and a query point in one of them, finds its corresponden ce in the other. By doing so, one has the option to query only the points of interest and retrieve sparse corresponden ces, or to query all points in an image and obtain dense mappings. Importantly, in order to capture both local and global priors, and to let our model relate between image regions using the most relevant among said priors, we realize our network using a transformer. At inference time, we apply our correspondence network by recursively zooming in around the estimates, yielding a multiscale pipeline able to provide highly-accurate correspondences. Our method significantly outperforms the state of the art on both sparse and dense correspondence problems on multiple datasets and tasks, ranging from wide-baseline stereo to optical flow, without any retraining for a specific dataset. We commit to releasing data, code, and all the tools necessary to train from scratch and ensure reproducibility.

我们提出了一种基于深度神经网络的新型框架，用于在图像中寻找对应关系。该框架在给定两幅图像及其中一幅的查询点时，能在另一幅图像中找到其对应位置。通过这种方式，可以选择仅查询感兴趣的点以获取稀疏对应关系，或查询图像中所有点以获得密集映射。重要的是，为了捕捉局部和全局先验，并让模型利用最相关的先验关联图像区域，我们采用Transformer架构实现网络。在推理阶段，通过递归放大估计区域来应用我们的对应网络，形成一个能够提供高精度对应关系的多尺度流程。我们的方法在多个数据集和任务（从宽基线立体匹配到光流）的稀疏与稠密对应问题上显著优于现有技术，且无需针对特定数据集重新训练。我们承诺公开数据、代码及所有必要工具，确保从头训练的可复现性。

1. Introduction

1. 引言

Finding correspondences across pairs of images is a fundamental task in computer vision, with applications ranging from camera calibration [22, 28] to optical flow [32, 15], Structure from Motion (SfM) [56, 28], visual localization [55, 53, 36], point tracking [35, 68], and human pose estimation [43, 20]. Traditionally, two fundamental research directions exist for this problem. One is to extract sets of sparse keypoints from both images and match them in order to minimize an alignment metric [33, 55, 28]. The other is to interpret correspondence as a dense process, where every pixel in the first image maps to a pixel in the second image [32, 60, 77, 72].

在计算机视觉中，寻找图像对之间的对应关系是一项基础任务，其应用涵盖相机标定 [22, 28]、光流 [32, 15]、运动恢复结构 (SfM) [56, 28]、视觉定位 [55, 53, 36]、点跟踪 [35, 68] 以及人体姿态估计 [43, 20] 等领域。传统上，针对该问题存在两个主要研究方向：一是从两幅图像中提取稀疏关键点集合并通过匹配最小化对齐度量 [33, 55, 28]；二是将对应关系视为密集过程，即第一幅图像的每个像素都映射到第二幅图像的某个像素 [32, 60, 77, 72]。

The divide between sparse and dense emerged naturally from the applications they were devised for. Sparse methods have largely been used to recover a single global camera motion, such as in wide-baseline stereo, using geometrical constraints. They rely on local features [34, 74, 44, 13] and further prune the putative correspondences formed with them in a separate stage with sampling-based robust matchers [18, 3, 12], or their learned counterparts [75, 7, 76, 64, 54]. Dense methods, by contrast, usually model small temporal changes, such as optical flow in video sequences, and rely on local smoothness [35, 24]. Exploiting context in this manner allows them to find correspondences at arbitrary locations, including seemingly texture-less areas.

稀疏与密集方法之间的区分源于它们各自设计的应用场景。稀疏方法主要用于通过几何约束恢复单一的全局相机运动，例如在宽基线立体视觉中。它们依赖于局部特征 [34, 74, 44, 13]，并通过基于采样的鲁棒匹配器 [18, 3, 12] 或其学习型变体 [75, 7, 76, 64, 54] 在独立阶段进一步修剪由这些特征形成的假设对应关系。相比之下，密集方法通常建模微小的时间变化，例如视频序列中的光流，并依赖于局部平滑性 [35, 24]。通过这种方式利用上下文，它们能够在任意位置（包括看似无纹理的区域）找到对应关系。

Figure 1. The Correspondence Transformer – (a) COTR formulates the correspondence problem as a functional mapping from point $x$ to point $\ensuremath{\boldsymbol{x}}^{\prime}$ , conditional on two input images $\pmb{I}$ and $\pmb{I}^{\prime}$ . (b) COTR is capable of sparse matching under different motion types, including camera motion, multi-object motion, and object-pose changes. (c) COTR generates a smooth correspondence map for stereo pairs: given (c.1,2) as input, (c.3) shows the predicted dense correspondence map (color-coded $\mathbf{\hat{\Sigma}}_{\mathbf{X}},$ channel), and (c.4) warps (c.2) onto (c.1) with the predicted correspondences.

图 1: Correspondence Transformer – (a) COTR 将对应关系问题表述为从点 $x$ 到点 $\ensuremath{\boldsymbol{x}}^{\prime}$ 的函数映射，条件是两个输入图像 $\pmb{I}$ 和 $\pmb{I}^{\prime}$。 (b) COTR 能够在不同运动类型下进行稀疏匹配，包括相机运动、多物体运动和物体姿态变化。 (c) COTR 为立体图像对生成平滑的对应关系图：给定 (c.1,2) 作为输入，(c.3) 显示了预测的密集对应关系图（颜色编码的 $\mathbf{\hat{\Sigma}}_{\mathbf{X}},$ 通道），(c.4) 使用预测的对应关系将 (c.2) 扭曲到 (c.1) 上。

In this work, we present a solution that bridges this divide, a novel network architecture that can express both forms of prior knowledge – global and local – and learn them implicitly from data. To achieve this, we leverage the inductive bias that densely connected networks possess in representing smooth functions [1, 4, 48] and use a transformer [73, 10, 14] to automatically control the nature of priors and learn how to utilize them through its attention mechanism. For example, ground-truth optical flow typically does not change smoothly across object boundaries, and simple (attention-agnostic) densely connected networks would have challenges in modelling such a discontinuous correspondence map, whereas a transformer would not. Moreover, transformers allow encoding the relationship between different locations of the input data, making them a natural fit for correspondence problems.

在这项工作中，我们提出了一种弥合这一鸿沟的解决方案——一种新颖的网络架构，能够同时表达全局和局部两种先验知识形式，并从数据中隐式学习这些知识。为实现这一目标，我们利用了密集连接网络在表示平滑函数时具有的归纳偏置 [1, 4, 48]，并采用 transformer [73, 10, 14] 来自动控制先验性质，通过其注意力机制学习如何利用这些先验。例如，真实光流通常在物体边界处不会平滑变化，简单的（不考虑注意力的）密集连接网络难以建模这种不连续的对应关系图，而 transformer 则能胜任。此外，transformer 可以编码输入数据不同位置之间的关系，使其天然适合对应关系问题。

Specifically, we express the problem of finding correspondences between images $\pmb{I}$ and $\pmb{I}^{\prime}$ in functional form, as $x^{\prime}=\mathcal{F}{\Phi}(x\mid I,I^{\prime})$ , where ${\mathcal{F}}{\Phi}$ is our neural network architecture, parameterized by $\Phi$ , ${x}$ indexes a query location in $\pmb{I}$ , and $\mathbf{\Delta}_{x^{\prime}}$ indexes its corresponding location in $\pmb{I}^{\prime}$ ; see Figure 1. Differently from sparse methods, COTR can match arbitrary query points via this functional mapping, predicting only as many matches as desired. Differently from dense methods, COTR learns smoothness implicitly and can deal with large camera motion effectively.

具体而言，我们将图像$\pmb{I}$与$\pmb{I}^{\prime}$间的对应关系搜索问题表述为函数形式$x^{\prime}=\mathcal{F}{\Phi}(x\mid I,I^{\prime})$。其中${\mathcal{F}}{\Phi}$是由$\Phi$参数化的神经网络架构，${x}$表示$\pmb{I}$中的查询位置，$\mathbf{\Delta}_{x^{\prime}}$表示其在$\pmb{I}^{\prime}$中的对应位置（见图1）。与稀疏方法不同，COTR通过这种函数映射可匹配任意查询点，仅需预测所需数量的匹配对。与稠密方法不同，COTR隐式学习平滑性，并能有效处理大幅相机运动。

Our work is the first to apply transformers to obtain accurate correspondences. Our main technical contributions are:

我们的工作是首个应用Transformer实现精确对应关系的研究。主要技术贡献包括：

• we propose a functional correspondence architecture that combines the strengths of dense and sparse methods; • we show how to apply our method recursively at multiple scales during inference in order to compute highlyaccurate correspondences; • we demonstrate that COTR achieves state-of-the-art performance in both dense and sparse correspondence problems on multiple datasets and tasks, without retraining; • we substantiate our design choices and show that the transformer is key to our approach by replacing it with a simpler model, based on a Multi-Layer Perceptron (MLP).

• 我们提出了一种结合稠密与稀疏方法优势的功能对应架构；
• 我们展示了如何在推理过程中递归应用多尺度方法以计算高精度对应关系；
• 实验证明 COTR 在多个数据集和任务中无需重新训练即可实现稠密与稀疏对应问题的当前最优性能；
• 通过用基于多层感知机 (MLP) 的简化模型替换 Transformer，我们验证了设计选择并表明 Transformer 是本方法的核心。

2. Related works

2. 相关工作

We review the literature on both sparse and dense matching, as well as works that utilize transformers for vision.

我们回顾了关于稀疏匹配和稠密匹配的文献，以及利用Transformer进行视觉研究的工作。

Sparse methods. Sparse methods generally consist of three stages: keypoint detection, feature description, and feature matching. Seminal detectors include DoG [34] and FAST [51]. Popular patch descriptors range from handcrafted [34, 9] to learned [42, 66, 17] ones. Learned feature extractors became popular with the introduction of LIFT [74], with many follow-ups [13, 44, 16, 49, 5, 71]. Local features are designed with sparsity in mind, but have also been applied densely in some cases [67, 32]. Learned local features are trained with intermediate metrics, such as descriptor distance or number of matches.

稀疏方法。稀疏方法通常包含三个阶段：关键点检测、特征描述和特征匹配。具有开创性的检测器包括 DoG [34] 和 FAST [51]。流行的块描述符涵盖从手工设计 [34, 9] 到学习型 [42, 66, 17] 的各种方法。随着 LIFT [74] 的引入，学习型特征提取器变得流行起来，并涌现出许多后续研究 [13, 44, 16, 49, 5, 71]。局部特征在设计时考虑了稀疏性，但在某些情况下也被密集应用 [67, 32]。学习型局部特征通过中间指标进行训练，例如描述符距离或匹配数量。

Feature matching is treated as a separate stage, where descriptors are matched, followed by heuristics such as the ratio test, and robust matchers, which are key to deal with high outlier ratios. The latter are the focus of much research, whether hand-crafted, following RANSAC [18, 12, 3], consensus- or motion-based heuristics [11, 31, 6, 37], or learned [75, 7, 76, 64]. The current state of the art builds on attention al graph neural networks [54]. Note that while some of these theoretically allow feature extraction and matching to be trained end to end, this avenue remains largely unexplored. We show that our method, which does not divide the pipeline into multiple stages and is learned end-to-end, can outperform these sparse methods.

特征匹配被视为一个独立阶段，首先进行描述符匹配，随后采用启发式方法（如比率检验）和鲁棒匹配器处理高异常值比率问题。后者是大量研究的核心方向，无论是基于RANSAC [18, 12, 3] 的手工设计方法，基于一致性或运动的启发式算法 [11, 31, 6, 37]，还是学习型方法 [75, 7, 76, 64]。当前最优方法建立在注意力图神经网络 (attention graph neural networks) [54] 基础上。值得注意的是，虽然其中部分方法理论上支持端到端训练特征提取与匹配，但该方向仍存在大量探索空间。我们证明，这种不分割处理流程且采用端到端学习的方法，其性能可超越现有稀疏方法。

Dense methods. Dense methods aim to solve optical flow. This typically implies small displacements, such as the motion between consecutive video frames. The classical LucasKanade method [35] solves for correspondences over local neighbourhoods, while Horn-Schunck [24] imposes global smoothness. More modern algorithms still rely on these principles, with different algorithmic choices [59], or focus on larger displacements [8]. Estimating dense correspond ences under large baselines and drastic appearance changes was not explored until methods such as DeMoN [72] and SfMLearner [77] appeared, which recovered both depth and camera motion – however, their performance fell somewhat short of sparse methods [75]. Neighbourhood Consensus Networks [50] explored 4D correlations – while powerful, this limits the image size they can tackle. More recently, DGC-Net [38] applied CNNs in a coarse-to-fine approach, trained on synthetic transformations, GLU-Net [69] combined global and local correlation layers in a feature pyramid, and GOCor [70] improved the feature correlation layers to disambiguate repeated patterns. We show that we outperform DGC-Net, GLU-Net and GOCor over multiple datasets, while retaining our ability to query individual points.

稠密方法。稠密方法旨在解决光流问题，通常适用于微小位移场景，例如连续视频帧之间的运动。经典LucasKanade方法[35]通过局部邻域求解对应关系，而Horn-Schunck[24]则施加全局平滑约束。现代算法仍基于这些原理，采用不同算法选择[59]，或专注于更大位移场景[8]。直到DeMoN[72]和SfMLearner[77]等方法出现，才首次探索了大基线和剧烈外观变化下的稠密对应估计——这些方法虽能同时恢复深度和相机运动，但性能略逊于稀疏方法[75]。邻域共识网络[50]探索了4D相关性，虽然强大但限制了可处理的图像尺寸。近期DGC-Net[38]采用由粗到细的CNN方法并在合成变换上训练，GLU-Net[69]在特征金字塔中结合全局与局部相关层，GOCor[70]则改进特征相关层以消除重复模式的歧义。我们证明在多个数据集上超越DGC-Net、GLU-Net和GOCor的同时，仍保持单点查询能力。

Attention mechanisms. The attention mechanism enables a neural network to focus on part of the input. Hard attention was pioneered by Spatial Transformers [26], which introduced a powerful differentiable sampler, and was later improved in [27]. Soft attention was pioneered by transformers [73], which has since become the de-facto standard in natural language processing – its application to vision tasks is still in its early stages. Recently, DETR [10] used Transformers for object detection, whereas ViT [14] applied them to image recognition. Our method is the first application of transformers to image correspondence problems.

注意力机制。注意力机制使神经网络能够聚焦于输入的部分内容。硬注意力 (hard attention) 由 Spatial Transformers [26] 首创，该研究引入了强大的可微分采样器，后续在 [27] 中得到改进。软注意力 (soft attention) 由 Transformer [73] 开创，现已成为自然语言处理领域的事实标准——其在视觉任务中的应用仍处于早期阶段。近期，DETR [10] 将 Transformer 应用于目标检测，而 ViT [14] 则将其用于图像识别。我们的方法是 Transformer 在图像对应问题中的首次应用。

Functional methods using deep learning. While the idea existed already, e.g. to generate images [58], using neural networks in functional form has recently gained much traction. DeepSDF [45] uses deep networks as a function that returns the signed distance field value of a query point. These ideas were recently extended by [21] to establish correspondences between incomplete shapes. While not directly related to image correspondence, this research has shown that functional methods can achieve state-of-the-art performance.

基于深度学习的函数式方法。虽然这一想法早已存在，例如用于生成图像[58]，但以函数形式使用神经网络最近获得了广泛关注。DeepSDF[45]将深度网络作为返回查询点有符号距离场值的函数。这些想法近期被[21]扩展应用于建立不完整形状之间的对应关系。尽管与图像对应没有直接关联，该研究证明了函数式方法能够实现最先进的性能。

3. Method

3. 方法

We first formalize our problem (Section 3.1), then detail our architecture (Section 3.2), its recursive use at inference time (Section 3.3), and our implementation (Section 3.4).

我们首先对问题进行形式化描述(第3.1节)，随后详细阐述架构设计(第3.2节)、推理阶段的递归调用机制(第3.3节)以及具体实现方案(第3.4节)。

3.1. Problem formulation

3.1. 问题表述

Let $\pmb{x}\in[0,1]^{2}$ be the normalized coordinates of the query point in image $\pmb{I}$ , for which we wish to find the corresponding point, $\pmb{x}^{\prime}\in[0,1]^{2}$ , in image $\pmb{I}^{\prime}$ . We frame the problem of learning to find correspondences as that of finding the best set of parameters $\Phi$ for a parametric function $\mathcal{F}_{\Phi}\left(x|I,I^{\prime}\right)$ minimizing

设 $\pmb{x}\in[0,1]^{2}$ 为图像 $\pmb{I}$ 中查询点的归一化坐标，我们希望找到其在图像 $\pmb{I}^{\prime}$ 中的对应点 $\pmb{x}^{\prime}\in[0,1]^{2}$。我们将学习寻找对应关系的问题表述为：寻找参数函数 $\mathcal{F}_{\Phi}\left(x|I,I^{\prime}\right)$ 的最优参数集 $\Phi$，以最小化

$$
\begin{array}{r l}&{\underset{\Phi}{\arg\operatorname*{min}}\underset{(\pmb{x},\pmb{x}^{\prime},I,I^{\prime})\sim\mathcal{D}}{\mathbb{E}}~\mathcal{L}{\mathrm{corr}}+\mathcal{L}_{\mathrm{cycle}},}\end{array}
$$

$$
\begin{array}{r l}&{\underset{\Phi}{\arg\operatorname*{min}}\underset{(\pmb{x},\pmb{x}^{\prime},I,I^{\prime})\sim\mathcal{D}}{\mathbb{E}}~\mathcal{L}{\mathrm{corr}}+\mathcal{L}_{\mathrm{cycle}},}\end{array}
$$

$$
\begin{array}{r l}&{\mathcal{L}{\mathrm{corr}}=\left|\pmb{x}^{\prime}-\mathcal{F}{\Phi}\left(\pmb{x}\mid\pmb{I},\pmb{I}^{\prime}\right)\right|{2}^{2},}\ &{\mathcal{L}{\mathrm{cycle}}=\left|\pmb{x}-\mathcal{F}{\Phi}\left(\mathcal{F}{\Phi}\left(\pmb{x}\mid\pmb{I},\pmb{I}^{\prime}\right)|\pmb{I},\pmb{I}^{\prime}\right)\right|_{2}^{2},}\end{array}
$$

$$
\begin{array}{r l}&{\mathcal{L}{\mathrm{corr}}=\left|\pmb{x}^{\prime}-\mathcal{F}{\Phi}\left(\pmb{x}\mid\pmb{I},\pmb{I}^{\prime}\right)\right|{2}^{2},}\ &{\mathcal{L}{\mathrm{cycle}}=\left|\pmb{x}-\mathcal{F}{\Phi}\left(\mathcal{F}{\Phi}\left(\pmb{x}\mid\pmb{I},\pmb{I}^{\prime}\right)|\pmb{I},\pmb{I}^{\prime}\right)\right|_{2}^{2},}\end{array}
$$

where $\mathcal{D}$ is the training dataset of ground correspondences, $\mathcal{L}{\mathrm{corr}}$ measures the correspondence estimation errors, and $\mathcal{L}_{\mathrm{cycle}}$ enforces correspondences to be cycle-consistent.

其中 $\mathcal{D}$ 是地面真实对应关系的训练数据集，$\mathcal{L}{\mathrm{corr}}$ 衡量对应关系估计误差，$\mathcal{L}_{\mathrm{cycle}}$ 强制要求对应关系保持循环一致性。

3.2. Network architecture

3.2. 网络架构

We implement ${\mathcal{F}}_{\Phi}$ with a transformer. Our architecture, inspired by [10, 14], is illustrated in Figure 2. We first crop and resize the input into a $256\times256$ image, and convert it into a down sampled feature map size $16\times16\times256$ with a shared CNN backbone, $\mathcal{E}$ . We then concatenate the representations for two corresponding images side by side, forming a feature map size $16\times32\times256$ , to which we add positional encoding $\mathcal{P}$ (with $N{=}256$ channels) of the coordinate function $\pmb{\Omega}$ (i.e. MeshGrid(0:1, 0:2) of size $16\times32\times2$ ) to produce a context feature map c (of size $16\times32\times256$ ):

我们使用一个Transformer来实现 ${\mathcal{F}}_{\Phi}$ 。我们的架构受到[10, 14]的启发，如图 2 所示。首先将输入裁剪并调整为 $256\times256$ 的图像，通过共享的CNN主干网络 $\mathcal{E}$ 将其转换为下采样特征图，尺寸为 $16\times16\times256$ 。然后将两幅对应图像的表示并排拼接，形成尺寸为 $16\times32\times256$ 的特征图，并为其添加坐标函数 $\pmb{\Omega}$ (即尺寸为 $16\times32\times2$ 的MeshGrid(0:1, 0:2))的位置编码 $\mathcal{P}$ (通道数为 $N{=}256$ )，从而生成上下文特征图c (尺寸为 $16\times32\times256$ ):

$$
\mathbf{c}=[\mathcal{E}(I),\mathcal{E}(I^{\prime})]+\mathcal{P}(\pmb{\Omega}),
$$

$$
\mathbf{c}=[\mathcal{E}(I),\mathcal{E}(I^{\prime})]+\mathcal{P}(\pmb{\Omega}),
$$

where $[\cdot]$ denotes concatenation along the spatial dimension – a subtly important detail novel to our architecture that we discuss in greater depth later on. We then feed the context feature map c to a transformer encoder $\tau_{\varepsilon}$ , and interpret its results with a transformer decoder $\tau_{\mathcal{D}}$ , along with the query point ${x}$ , encoded by $\mathcal{P}$ – the positional encoder used to generate $\pmb{\Omega}$ . We finally process the output of the transformer decoder with a fully connected layer $\mathcal{D}$ to obtain our estimate for the corresponding point, $\mathbf{\Delta}{x^{\prime}}$ .

其中 $[\cdot]$ 表示沿空间维度的拼接操作 (这是我们架构中一个微妙而重要的创新细节，后文将深入探讨)。随后，我们将上下文特征图 c 输入到 Transformer 编码器 $\tau_{\varepsilon}$ 中，并通过 Transformer 解码器 $\tau_{\mathcal{D}}$ 结合查询点 ${x}$ (由位置编码器 $\mathcal{P}$ 编码生成，该编码器用于生成 $\pmb{\Omega}$) 来解读其结果。最后，我们使用全连接层 $\mathcal{D}$ 处理 Transformer 解码器的输出，以获得对应点 $\mathbf{\Delta}{x^{\prime}}$ 的估计值。

$$
\begin{array}{r}{\pmb{x}^{\prime}=\mathcal{F}_{\pmb{\Phi}}\left(\pmb{x}|\pmb{I},\pmb{I}^{\prime}\right)=\mathcal{D}\left(\mathcal{T}_{\mathcal{D}}\left(\mathcal{P}\left(\pmb{x}\right),\mathcal{T}_{\mathcal{E}}\left(\mathbf{c}\right)\right)\right).}\end{array}
$$

$$
\begin{array}{r}{\pmb{x}^{\prime}=\mathcal{F}_{\pmb{\Phi}}\left(\pmb{x}|\pmb{I},\pmb{I}^{\prime}\right)=\mathcal{D}\left(\mathcal{T}_{\mathcal{D}}\left(\mathcal{P}\left(\pmb{x}\right),\mathcal{T}_{\mathcal{E}}\left(\mathbf{c}\right)\right)\right).}\end{array}
$$

For architectural details of each component please refer to supplementary material.

各组件架构详情请参阅补充材料。

Importance of context concatenation. Concatenation of the feature maps along the spatial dimension is critical, as it allows the transformer encoder $\tau_{\varepsilon}$ to relate between locations within the image (self-attention), and across images (cross-attention). Note that, to allow the encoder to distinguish between pixels in the two images, we employ a single positional encoding for the entire concatenated feature map; see Fig. 2. We concatenate along the spatial dimension rather than the channel dimension, as the latter would create artificial relationships between features coming from the same pixel locations in each image. Concatenation allows the features in each map to be treated in a way that is similar to words in a sentence [73]. The encoder then associates and relates them to discover which ones to attend to given their context – which is arguably a more natural way to find correspondences.

上下文拼接的重要性。沿空间维度对特征图进行拼接至关重要，这使得Transformer编码器$\tau_{\varepsilon}$能够建立图像内部位置（自注意力）和跨图像（交叉注意力）之间的关联。需要注意的是，为了让编码器能区分两幅图像中的像素，我们对整个拼接后的特征图采用单一位置编码（参见图2）。选择沿空间维度而非通道维度进行拼接，是因为后者会在来自两幅图像相同像素位置的特征之间建立人为关联。这种拼接方式使每个特征图中的特征能够以类似句子中词语处理的方式被对待[73]。编码器随后会根据上下文对这些特征进行关联和筛选，从而以更自然的方式发现对应关系。

Figure 2. The COTR architecture – We first process each image with a (shared) backbone CNN $\mathcal{E}$ to produce feature maps size 16x16, which we then concatenate together, and add positional encodings to form our context feature map. The results are fed into a transformer $\tau$ , along with the query point(s) ${\pmb{x}}$ . The output of the transformer is decoded by a multi-layer perceptron $\mathcal{D}$ into correspondence(s) $\mathbf{\Delta}_{x^{\prime}}$ .

图 2: COTR架构 - 我们首先使用(共享的)主干CNN网络$\mathcal{E}$处理每张图像，生成16x16大小的特征图，随后将这些特征图拼接在一起并添加位置编码，形成上下文特征图。处理结果与查询点${\pmb{x}}$一起输入到Transformer网络$\tau$中。Transformer的输出通过多层感知机$\mathcal{D}$解码为对应关系$\mathbf{\Delta}_{x^{\prime}}$。

Linear positional encoding. We found it critical to use a linear increase in frequency for the positional encoding, as opposed to the commonly used log-linear strategy [73, 10], which made our optimization unstable; see supplementary material. Hence, for a given location $\pmb{x}=[x,y]$ we write

线性位置编码。我们发现，与常用的对数线性策略 [73, 10] 不同，采用频率线性增长的位置编码对优化稳定性至关重要；详见补充材料。因此，对于给定位置 $\pmb{x}=[x,y]$，我们采用线性编码方式。

$$
\begin{array}{r l}&{\mathcal{P}(\pmb{x})=\left[p_{1}(\pmb{x}),p_{2}(\pmb{x}),\dots,p_{\frac{N}{4}}(\pmb{x})\right],}\ &{p_{k}(\pmb{x})=\left[\sin(k\pi\pmb{x}^{\top}),\cos(k\pi\pmb{x}^{\top})\right],}\end{array}
$$

$$
\begin{array}{r l}&{\mathcal{P}(\pmb{x})=\left[p_{1}(\pmb{x}),p_{2}(\pmb{x}),\dots,p_{\frac{N}{4}}(\pmb{x})\right],}\ &{p_{k}(\pmb{x})=\left[\sin(k\pi\pmb{x}^{\top}),\cos(k\pi\pmb{x}^{\top})\right],}\end{array}
$$

where $N=256$ is the number of channels of the feature map. Note that $p_{k}$ generates four values, so that the output of the encoder $\mathcal{P}$ is size $N$ .

其中 $N=256$ 是特征图的通道数。注意 $p_{k}$ 会生成四个值，因此编码器 $\mathcal{P}$ 的输出尺寸为 $N$。

Querying multiple points. We have introduced our framework as a function operating on a single query point, ${x}$ . However, as shown in Fig. 2, extending it to multiple query points is straightforward. We can simply input multiple queries at once, which the transformer decoder $\tau{\mathcal{D}}$ and the decoder $\mathcal{D}$ will translate into multiple coordinates. Importantly, while doing so, we disallow self attention among the query points in order to ensure that they are solved independently.

查询多点。我们的框架最初是作为针对单个查询点 ${x}$ 的函数提出的。但如图 2 所示，将其扩展到多个查询点非常简单：只需一次性输入多个查询，Transformer解码器 $\tau{\mathcal{D}}$ 和解码器 $\mathcal{D}$ 就会将其转换为多个坐标。关键的是，在此过程中我们会禁止查询点之间的自注意力机制 (self attention) ，以确保各查询点被独立求解。

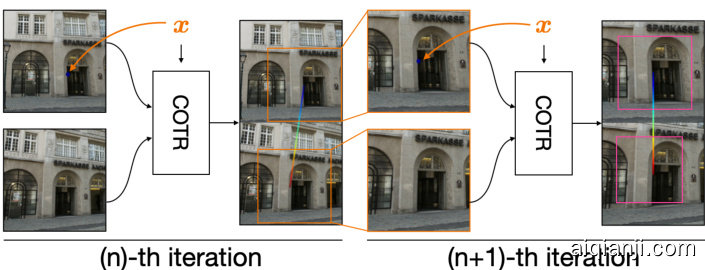
Figure 3. Recursive COTR at inference time – We obtain accurate correspondences by applying our functional approach recursively, zooming into the results of the previous iteration, and running the same network on the pair of zoomed-in crops. We gradually focus on the correct correspondence, with greater accuracy.

图 3: 推理时的递归 COTR —— 我们通过递归应用函数式方法，放大前一次迭代的结果，并在放大后的图像对上运行相同网络，从而获得精确对应关系。随着逐步聚焦于正确对应点，精度也随之提升。

3.3. Inference

3.3. 推理

We next discuss how to apply our functional approach at inference time in order to obtain accurate correspondences.

接下来我们将讨论如何在推理时应用我们的功能方法以获得准确的对应关系。

Inference with recursive with zoom-in. Applying the powerful transformer attention mechanism to vision problems comes at a cost – it requires heavily down sampled feature maps, which in our case naturally translates to poorly localized correspondences; see Section 4.6. We address this by exploiting the functional nature of our approach, applying out network ${\mathcal{F}}_{\Phi}$ recursively. As shown in Fig. 3, we iteratively zoom into a previously estimated correspondence, on both images, in order to obtain a refined estimate. There is a trade-off between compute and the number of zoom-in steps. We ablated this carefully on the validation data and settled on a zoom-in factor of two at each step, with four zoom-in steps. It is worth noting that multiscale refinement is common in many computer vision algorithms [32, 15], but thanks to our functional correspondence model, realizing such a multiscale inference process is not only possible, but also straightforward to implement.

递归放大推理。将强大的Transformer注意力机制应用于视觉问题需要付出代价——它需要大幅下采样的特征图，这在本研究中自然会导致定位对应关系不准确（详见第4.6节）。我们通过利用方法的功能特性，递归应用网络${\mathcal{F}}_{\Phi}$来解决这个问题。如图3所示，我们在两幅图像上对先前估计的对应点进行迭代放大，以获得更精确的估计结果。计算量与放大步骤数之间存在权衡关系，我们在验证数据上进行了细致消融实验，最终确定每步放大两倍，共进行四次放大。值得注意的是，多尺度优化是许多计算机视觉算法的常见策略[32,15]，而得益于我们的函数式对应模型，实现这种多尺度推理过程不仅可行，而且实现起来非常直观。

Compensating for scale differences. While matching images recursively, one must account for a potential mismatch in scale between images. We achieve this by making the scale of the patch to crop proportional to the commonly visible regions in each image, which we compute on the first step, using the whole images. To extract this region, we compute the cycle consistency error at the coarsest level, for every pixel, and threshold it at $\tau_{\mathrm{visible}}{=}5$ pixels on the $256\times256$ image; see Fig. 4. In subsequent stages – the zoom-ins – we simply adjust the crop sizes over $\pmb{I}$ and $\pmb{I}^{\prime}$ so that their relationship is proportional to the sum of valid pixels (the unmasked pixels in Fig. 4).

补偿尺度差异。在递归匹配图像时，必须考虑图像间可能存在的尺度不匹配问题。我们通过使裁剪的图块(patch)尺度与每张图像中共同可见区域成比例来实现这一点，该比例关系在第一步使用完整图像计算得出。为提取该区域，我们在最粗粒度层级为每个像素计算循环一致性误差(cycle consistency error)，并在$256\times256$图像上以$\tau_{\mathrm{visible}}{=}5$像素为阈值进行二值化处理（见图4）。在后续放大阶段，我们仅需调整$\pmb{I}$和$\pmb{I}^{\prime}$的裁剪尺寸，使其比例关系与有效像素（图4中未掩膜像素）数量总和保持一致。

Dealing with images of arbitrary size. Our network expects images of fixed $256\times256$ shape. To process images of arbitrary size, in the initial step we simply resize (i.e. stretch) them to $256\times256$ , and estimate the initial correspondences. In subsequent zoom-ins, we crop square patches from the original image around the estimated points, of a size commensurate with the current zoom level, and resize them to

处理任意尺寸的图像。我们的网络要求输入固定为 $256\times256$ 尺寸的图像。为处理任意尺寸的图像，初始步骤中我们简单地将其缩放（即拉伸）至 $256\times256$ 并估算初始对应关系。在后续的放大步骤中，我们从原始图像中围绕估算点裁剪出与当前缩放级别相匹配的正方形区域，并将其缩放至

Figure 4. Estimating scale by finding co-visible regions – We show two images we wish to put in correspondence, and the estimated regions in common – image locations with a high cycleconsistency error are masked out.

图 4: 通过寻找共视区域估计尺度——我们展示了两幅需要建立对应关系的图像及其估计的共有区域 (cycle-consistency误差较高的图像区域被掩膜处理)。

$256\times256$ . While this may seem a limitation on images with non-standard aspect ratios, our approach performs well on KITTI, which are extremely wide (3.3:1). Moreover, we present a strategy to tile detections in Section 4.4.

$256\times256$。虽然这看似限制了非标准宽高比的图像，但我们的方法在极宽比例(3.3:1)的KITTI数据集上表现良好。此外，我们将在4.4节提出一种分块检测策略。

Discarding erroneous correspondences. What should we do when we query a point is occluded or outside the viewport in the other image? Similarly to our strategy to compensate for scale, we resolve this problem by simply rejecting correspondences that induce a cycle consistency error (3) greater than $\tau_{\mathrm{cycle}}=5$ pixels. Another heuristic we apply is to terminate correspondences that do not converge while zooming in. We compute the standard deviation of the zoom-in estimates, and reject correspondences that oscillate by more than $\tau_{\mathrm{std}}{=}0.02$ of the long-edge of the image.

丢弃错误对应关系。当查询点在另一图像中被遮挡或位于视口外时，我们该如何处理？与补偿尺度的策略类似，我们通过直接拒绝循环一致性误差 (3) 超过 $\tau_{\mathrm{cycle}}=5$ 像素的对应关系来解决此问题。另一个启发式方法是终止在放大过程中未收敛的对应关系。我们计算放大估计的标准差，并拒绝振荡幅度超过图像长边 $\tau_{\mathrm{std}}{=}0.02$ 的对应关系。

Interpolating for dense correspondence. While we could query every single point in order to obtain dense estimates, it is also possible to densify matches by computing sparse matches first, and then interpolating using bary centric weights on a Delaunay triangulation of the queries. This interpolation can be done efficiently using a GPU rasterizer.

插值实现密集对应。虽然我们可以查询每个点来获取密集估计，但也可以通过先计算稀疏匹配，然后在查询点的Delaunay三角剖分上使用重心权重进行插值来实现匹配的密集化。这种插值可以使用GPU光栅化器高效完成。

3.4. Implementation details

3.4. 实现细节

Datasets. We train our method on the MegaDepth dataset [30], which provides both images and corresponding dense depth maps, generated by SfM [56]. These images come from photo-tourism and show large variations in appearance and viewpoint, which is required to learn invariant models. The accuracy of the depth maps is sufficient to learn accurate local features, as demonstrated by [16, 54, 71]. To find co-visible pairs of images we can train with, we first filter out those with no common 3D points in the SfM model. We then compute the common area between the remaining pairs of images, by projecting pixels from one image to the other. Finally, we compute the intersection over union of the projected pixels, which accounts for different image sizes. We keep, for each image, the 20 image pairs with the largest overlap. This simple procedure results in a good combination of images with a mixture of high/low overlap. We use 115 scenes for training and 1 scene for validation.

数据集。我们在MegaDepth数据集[30]上训练我们的方法，该数据集提供了由SfM[56]生成的图像和相应的密集深度图。这些图像来自照片旅游，展示了外观和视角的巨大变化，这是学习不变模型所必需的。如[16,54,71]所示，深度图的准确性足以学习精确的局部特征。为了找到可以训练的共视图像对，我们首先过滤掉SfM模型中没有共同3D点的图像对。然后，我们通过将像素从一个图像投影到另一个图像来计算剩余图像对之间的共同区域。最后，我们计算投影像素的交并比，以考虑不同的图像大小。对于每个图像，我们保留重叠面积最大的20个图像对。这种简单的程序产生了高/低重叠混合的良好图像组合。我们使用115个场景进行训练，1个场景进行验证。

Implementation. We implement our method in PyTorch [46]. For the backbone $\mathcal{E}$ we use a ResNet50 [23], initialized with weights pre-trained on ImageNet [52]. We use the feature map after its fourth down sampling step (after the third residual block), which is of size $16\times16\times1024.$ , which we convert into $16\times16\times256$ with $1\times1$ convolutions. For the transformer, we use 6 layers for both encoder and decoder. Each encoder layer contains a self-attention layer with 8 heads, and each decoder layer contains an encoder-decoder attention layer with 8 heads, but with no self-attention layers, in order to prevent query points from communicating between each other. Finally, for the network that converts the Transformer output into coordinates, $\mathcal{D}$ , we use a 3-layer MLP, with 256 units each, followed by ReLU activation s.

实现。我们使用PyTorch [46] 实现了我们的方法。对于主干网络 $\mathcal{E}$，我们采用了在ImageNet [52] 上预训练的ResNet50 [23]，并取其第四次下采样后的特征图（位于第三个残差块之后），尺寸为 $16\times16\times1024$，随后通过 $1\times1$ 卷积将其转换为 $16\times16\times256$。在Transformer部分，编码器和解码器均使用6层结构。每个编码器层包含一个8头自注意力层，而每个解码器层则包含一个8头编码器-解码器注意力层（不设自注意力层），以避免查询点之间的信息交互。最后，用于将Transformer输出转换为坐标的网络 $\mathcal{D}$ 采用3层MLP（每层256个单元）并接ReLU激活函数。

On-the-fly training data generation. We select training pairs randomly, pick a random query point in the first image, and find its corresponding point on the second image using the ground truth depth maps. We then select a random zoom level among one of ten levels, uniformly spaced, in log scale, between $1\times$ and $10\times$ . We then crop a square patch at the desired zoom level, centered at the query point, from the first image, and a square patch that contains the corresponding point in the second image. Given this pair of crops, we sample 100 random valid correspondences across the two crops – if we cannot gather at least 100 valid points, we discard the pair and move to the next.

动态生成训练数据。我们随机选择训练样本对，在第一张图像中随机选取一个查询点，并使用真实深度图在第二张图像中找到其对应点。随后在$1\times$到$10\times$的对数尺度范围内，从十个均匀分布的缩放级别中随机选择一个级别。接着以查询点为中心，从第一张图像中裁剪出指定缩放倍率的方形图像块，并在第二张图像中裁剪出包含对应点的方形图像块。针对每对图像块，我们在两者之间随机采样100组有效对应点——若无法采集至少100组有效点，则丢弃该样本对并处理下一组数据。

Staged training. Our model is trained in three stages. First, we freeze the pre-trained backbone $\mathcal{E}$ , and train the rest of the network, for $300\mathrm{k\Omega}$ iterations, with the ADAM optimizer [29], a learning rate of $10^{-4}$ , and a batch size of 24. We then unfreeze the backbone and fine-tune everything endto-end with a learning rate of $10^{-5}$ and a batch size of 16, to accommodate the increased memory requirements, for 2M iterations, at which point the validation loss plateaus. Note that in the first two stages we use the whole images, resized to $256\times256$ , as input, which allows us to load the entire dataset into memory. In the third stage we introduce zoom-ins, generated as explained above, and train everything end-to-end for a further $300\mathrm{k}$ iterations.

分阶段训练。我们的模型分三个阶段进行训练。首先，冻结预训练主干网络$\mathcal{E}$，用ADAM优化器[29]、学习率$10^{-4}$、批量大小24训练网络其余部分$300\mathrm{k\Omega}$次迭代。随后解冻主干网络，以学习率$10^{-5}$、批量大小16（为适应更高的内存需求）端到端微调全部网络200万次迭代，直至验证损失趋于平稳。需注意的是，前两个阶段我们使用调整为$256\times256$的完整图像作为输入，这使得我们可以将整个数据集加载到内存中。第三阶段引入上文所述的缩放区域，并端到端训练所有组件额外$300\mathrm{k}$次迭代。

4. Results

4. 结果

We evaluate our method with four different datasets, each aimed for a different type of correspondence task. We do not perform any kind of re-training or fine-tuning. They are:

我们用四个不同的数据集评估了我们的方法，每个数据集针对不同类型的对应任务。我们没有进行任何形式的重新训练或微调。这些数据集包括：

• HPatches [2]: A dataset with planar surfaces viewed under different angles/illumination settings, and ground-truth homograph ies. We use this dataset to compare against dense methods that operate on the entire image. • KITTI [19]: A dataset for autonomous driving, where the ground-truth 3D information is collected via LIDAR. With this dataset we compare against dense methods on complex scenes with camera and multi-object motion. • ETH3D [57]: A dataset containing indoor and outdoor scenes captured using a hand-held camera, registered with SfM. As it contains video sequences, we use it to evaluate how methods perform as the baseline widens by increasing the interval between samples, following [69].

• HPatches [2]: 一个包含不同视角/光照条件下平面表面的数据集，并提供真实单应性变换。我们使用该数据集与基于整幅图像的密集方法进行对比。
• KITTI [19]: 用于自动驾驶的数据集，通过激光雷达 (LIDAR) 采集真实3D信息。我们在此数据集上对比相机和多目标运动复杂场景中的密集方法。
• ETH3D [57]: 包含手持相机拍摄的室内外场景数据集，采用运动恢复结构 (SfM) 进行配准。由于包含视频序列，我们参照 [69] 的方法，通过增加采样间隔来评估基线扩大时各算法的性能表现。

方法	AEPE Ex	PCK-1px↑	PCK-3px↑	PCK-5px↑
LiteFlowNet[25] CVPR'18	118.85	13.91	-	31.64
PWC-Net[61,62] CVPR'18, TPAMI'19	96.14	13.14	-	37.14
DGC-Net [38] WACV'19	33.26	12.00	-	58.06
GLU-Net[69] CVPR'20	25.05	39.55	71.52	78.54
GLU-Net+GOCor[70] NeurIPS'20	20.16	41.55	-	81.43
COTR	7.75	40.91	82.37	91.10
COTR+Interp.	7.98	33.08	77.09	86.33

Table 1. Quantitative results on HPatches – We report Average End Point Error (AEPE) and Percent of Correct Keypoints (PCK) with different thresholds. For PCK-1px and PCK-5px, we use the numbers reported in literature. We bold the best method and underline the second best.

表 1: HPatches定量评估结果 - 我们报告了不同阈值下的平均端点误差 (AEPE) 和正确关键点百分比 (PCK)。对于PCK-1px和PCK-5px指标，我们采用文献报道的数据。最佳方法用粗体标出，次优方法以下划线标示。

• Image Matching Challenge (IMC2020) [28]: A dataset and challenge containing wide-baseline stereo pairs from photo-tourism images, similar to those we use for training (on MegaDepth). It takes matches as input and measures the quality the poses estimated using said matches. We evaluate our method on the test set and compare against the state of the art in sparse methods.

• Image Matching Challenge (IMC2020) [28]: 一个包含来自照片旅游图像的宽基线立体对数据集及挑战赛，与我们用于训练的数据集 (MegaDepth) 类似。它以匹配点作为输入，并评估基于这些匹配点估计的位姿质量。我们在测试集上评估了该方法，并与稀疏方法领域的先进技术进行了对比。

4.1. HPatches

4.1. HPatches

We follow the evaluation protocol of [69, 70], which computes the Average End Point Error (AEPE) for all valid pixels, and the Percentage of Correct Keypoints (PCK) at a given re projection error threshold – we use 1, 3, and 5 pixels. Image pairs are generated taking the first (out of six) images for each scene as reference, which is matched against the other five. We provide two results for our method: ‘COTR’, which uses 1,000 random query points for each image pair, and ‘COTR $^+$ Interp.’, which interpolates correspondences for the remaining pixels using the strategy presented in Section 3.3. We report our results in Table 1.

我们遵循[69, 70]的评估协议，计算所有有效像素的平均端点误差(AEPE)，以及在给定重投影误差阈值下的正确关键点百分比(PCK)——我们使用1、3和5像素作为阈值。图像对生成时，将每个场景的六张图像中的第一张作为参考图像，并与其他五张进行匹配。我们为方法提供了两种结果："COTR"（每对图像使用1,000个随机查询点）和"COTR$^+$ Interp."（使用第3.3节提出的策略对剩余像素的对应关系进行插值）。结果如 表1 所示。

Our method provides the best results, with and without interpolation, with the exception of PCK-1px, where it remains close to the best baseline. We note that the results for this threshold should be taken with a grain of salt, as several scenes do not satisfy the planar assumption for all pixels. To provide some evidence for this, we reproduce the results for GLU-Net [69] using the code provided by the authors to measure PCK at 3 pixels, which was not computed in the paper. 2 COTR outperforms it by a significant margin.

我们的方法在有无插值情况下均能提供最佳结果，唯独在PCK-1px指标上略逊于最优基线。需要说明的是，该阈值下的结果需谨慎看待，因为部分场景的像素并不完全满足平面假设。为佐证这一点，我们使用作者提供的代码复现了GLU-Net[69]在3像素阈值下的PCK指标（原论文未计算该数据），结果显示COTR以显著优势胜出。

4.2. KITTI

4.2. KITTI

To evaluate our method in an environment more complex than simple planar scenes, we use the KITTI dataset [39, 40]. Following [70, 65], we use the training split for this evaluation, as ground-truth for the test split remains private – all methods, including ours, were trained on a separate dataset. We report results both in terms of AEPE, and ‘Fl.’ – the

为了在比简单平面场景更复杂的环境中评估我们的方法，我们使用了KITTI数据集 [39, 40]。参照 [70, 65] 的做法，本次评估采用训练集划分，因为测试集的真实数据仍未公开——包括本方法在内的所有模型均在独立数据集上完成训练。我们同步汇报了AEPE和"Fl."两项指标结果——

Figure 5. Qualitative examples on KITTI – We show the optical flow and its corresponding error map (“jet” color scheme) for three examples from KITTI-2015, with GLU-Net [69] as a baseline. COTR successfully recovers both the global motion in the scene, and the movement of individual objects, even when nearby cars move in opposite directions (top) or partially occlude each other (bottom).

图 5: KITTI定性示例 – 我们展示了KITTI-2015中三个样本的光流及其对应误差图("jet"配色方案)，以GLU-Net [69]作为基线。COTR成功恢复了场景中的全局运动以及单个物体的移动，即使相邻车辆朝相反方向运动(顶部)或部分相互遮挡(底部)。

方法	KITTI-2012	KITTI-2015
	AEPE↓	F1[%]↓
LiteFlowNet[25] CVPR'18	4.00	17.47
PWC-Net[61,62] CVPR'18, TPAMI'19	4.14	20.28
DGC-Net[38] WACV'19	8.50	32.28
GLU-Net[69] CVPR'20	3.34	18.93
RAFT[65] ECCV'20	2.15	9.30
GLU-Net+GOCor[70] NeurIPS'20	2.68	15.43
COTR3	1.28	7.36
COTR+Interp.	2.26	10.50

Table 2. Quantitative results on KITTI – We report the Average End Point