Imagining The Road Ahead: Multi-Agent Trajectory Prediction via Differentiable Simulation
展望前路:基于可微分模拟的多智能体轨迹预测
Abstract— We develop a deep generative model built on a fully differentiable simulator for multi-agent trajectory prediction. Agents are modeled with conditional recurrent variation al neural networks (CVRNNs), which take as input an ego-centric birdview image representing the current state of the world and output an action, consisting of steering and acceleration, which is used to derive the subsequent agent state using a kinematic bicycle model. The full simulation state is then different i ably rendered for each agent, initiating the next time step. We achieve state-of-the-art results on the INTERACTION dataset, using standard neural architectures and a standard variation al training objective, producing realistic multi-modal predictions without any ad-hoc diversity-inducing losses. We conduct ablation studies to examine individual components of the simulator, finding that both the kinematic bicycle model and the continuous feedback from the birdview image are crucial for achieving this level of performance. We name our model ITRA, for “Imagining the Road Ahead”.
摘要—我们开发了一种基于完全可微分模拟器的深度生成模型,用于多智能体轨迹预测。智能体采用条件循环变分神经网络(CVRNN)建模,该网络以代表当前世界状态的以自我为中心的鸟瞰图像作为输入,并输出由转向和加速度组成的动作,通过运动学自行车模型推导出后续智能体状态。随后为每个智能体可微分地渲染完整模拟状态,启动下一时间步。我们在INTERACTION数据集上取得了最先进的结果,使用标准神经架构和标准变分训练目标,无需任何临时多样性诱导损失即可生成真实的多模态预测。我们通过消融实验检验模拟器的各个组件,发现运动学自行车模型和来自鸟瞰图像的连续反馈对于实现此性能水平都至关重要。我们将模型命名为ITRA,意为"预想前方道路"。
I. INTRODUCTION
I. 引言
Predicting where other vehicles and roadway users are going to be in the next few seconds is a critical capability for autonomous vehicles at level three and above [1], [2]. Such models are typically deployed on-board in autonomous vehicles to facilitate safe path planning. Crucially, achieving safety requires such predictions to be diverse and multimodal, to account for all reasonable human behaviors, not just the most common ones. [3], [4].
预测其他车辆和道路使用者未来几秒的行驶位置是三级及以上自动驾驶汽车的关键能力 [1], [2]。这类模型通常部署在自动驾驶车辆的车载系统中,以实现安全的路径规划。关键在于,要确保安全性,这些预测必须具有多样性和多模态性,以涵盖所有合理的人类行为,而不仅仅是最常见的行为 [3], [4]。
Most of the existing approaches to trajectory prediction [5], [6], [7], [8], [9] treat it as a regression problem, encoding past states of the world to produce a distribution over trajectories for each agent in a relatively black-box manner, without accounting for future interactions. Several notable papers [10], [11], [12], [13] explicitly model trajectory generation as a sequential decision-making process, allowing the agents to interact in the future. In this work, we take this approach a step further, embedding a complete, but simple and cheap, simulator into our predictive models. The simulator accounts not only for the positions of different agents, but also their orientations, sizes, kinematic constraints on their motion, and provides a perception mechanism that renders the world as a birdview RGB image. Our entire model, including the simulator, is end-to-end differentiable and runs entirely on a GPU, enabling efficient training by gradient descent.
现有大多数轨迹预测方法 [5], [6], [7], [8], [9] 将其视为回归问题,以相对黑盒的方式编码历史状态来生成每个智能体的轨迹分布,而未考虑未来交互。若干重要论文 [10], [11], [12], [13] 将轨迹生成显式建模为序列决策过程,允许智能体在未来进行交互。本研究进一步推进该方法,将完整但轻量化的模拟器嵌入预测模型。该模拟器不仅考虑不同智能体的位置,还包含其朝向、尺寸、运动学约束,并提供将环境渲染为鸟瞰RGB图像的感知机制。整个模型(含模拟器)端到端可微分且完全在GPU上运行,支持通过梯度下降进行高效训练。
Each agent in our model is a separate conditional variational recurrent neural network (CVRNN), sharing network parameters across agents, which takes as input the birdview image provided by the simulator and outputs an action that is fed into the simulator. We use simple, well-established convolutional and recurrent neural architectures and train them entirely by maximum likelihood, using the tools of variation al inference [14], [15]. We do not rely on any adhoc feat uri z ation, problem-specific neural architectures, or diversity-inducing losses and still achieve new state-of-theart performance and realistic multi-modal predictions, as shown in Figure 1.
我们模型中的每个智能体都是一个独立的条件变分循环神经网络 (CVRNN),各智能体间共享网络参数。该网络以模拟器提供的鸟瞰图像作为输入,输出一个动作反馈给模拟器。我们采用简单成熟的卷积和循环神经网络架构,完全通过最大似然法进行训练,并运用变分推断工具 [14][15]。如图 1 所示,我们无需依赖任何临时特征工程、针对特定问题的神经架构或多样性诱导损失函数,仍能实现最先进的性能表现和真实的多模态预测。
We evaluate the resulting model, which we call ITRA for “Imagining the Road Ahead”, on the challenging INTERACTION dataset [16] which itself is composed of highly interactive motions of road agents in a variety of driving scenarios in locations from different countries. ITRA outperforms all the published baselines, including the winners of the recently completed INTERPRET Challenge [17].
我们在具有挑战性的INTERACTION数据集[16]上评估了最终模型(将其命名为ITRA,即"预判前路(Imagining the Road Ahead)")。该数据集本身由来自不同国家、多种驾驶场景下道路参与者的高度交互运动轨迹组成。ITRA的表现优于所有已发布的基线模型,包括近期结束的INTERPRET挑战赛[17]的优胜方案。
II. BACKGROUND
II. 背景
A. Problem Formulation
A. 问题描述
We assume that there are $N$ agents, where $N$ varies between test cases. At time $t\in{1,\ldots,T}$ each agent $i\in{1,\dots,N}$ is described by a 4-dimensional state vector $s_{t}^{i}=\big(x_{t}^{i},y_{t}^{i},\psi_{t}^{i},v_{t}^{i}\big)$ , which includes the agents’ position, orientation, and speed in a fixed global frame of reference. Each agent is additionally characterised by its immutable length $l^{i}$ and width $w^{i}$ . We write $s_{t}=(s_{t}^{1},\ldots,s_{t}^{N})$ for the joint state of all agents at time $t$ . The goal is to predict future trajectories $s_{t}^{i}$ for $t\in T_{o b s}+1:T$ and $i\in1:N$ , based on past states $1:T_{o b s}$ . This prediction task can technically can be framed as a regression problem, and as such, in principle, could be solved by any regression algorithm. We find, however, that it is beneficial to exploit the natural factorization of the problem in time and across agents, and to incorporate some domain knowledge in a form of a simulator.
我们假设存在 $N$ 个智能体 (agent),其中 $N$ 在不同测试案例中会变化。在时刻 $t\in{1,\ldots,T}$,每个智能体 $i\in{1,\dots,N}$ 由一个4维状态向量 $s_{t}^{i}=\big(x_{t}^{i},y_{t}^{i},\psi_{t}^{i},v_{t}^{i}\big)$ 描述,包含该智能体在固定全局参考系中的位置、朝向和速度。每个智能体还具有不可变的长度 $l^{i}$ 和宽度 $w^{i}$ 属性。我们用 $s_{t}=(s_{t}^{1},\ldots,s_{t}^{N})$ 表示时刻 $t$ 所有智能体的联合状态。目标是根据历史状态 $1:T_{o b s}$,预测未来时段 $t\in T_{o b s}+1:T$ 内所有智能体 $i\in1:N$ 的轨迹 $s_{t}^{i}$。从技术角度看,该预测任务可被表述为回归问题,因此原则上可通过任何回归算法求解。但我们发现,利用该问题在时间和智能体维度上的自然分解特性,并以模拟器 (simulator) 形式融入领域知识会带来显著优势。
B. Kinematic Bicycle Model
B. 运动自行车模型
The bicycle kinematic model [18], depicted in Figure 2, is known to be an accurate model of vehicle motion when not skidding or sliding and we found it to near-perfectly describe the trajectories of vehicles in the INTERACTION dataset. The action space in the bicycle model consists of steering and acceleration. We provide detailed equations of motion and discuss the procedure for fitting the bicycle model in the Appendix.
自行车运动学模型 [18] 如图 2 所示,已知是车辆在不打滑或侧滑时的精确运动模型,我们发现它几乎完美地描述了 INTERACTION 数据集中车辆的轨迹。该自行车模型的动作空间由转向和加速组成。我们在附录中提供了详细的运动方程,并讨论了拟合自行车模型的步骤。
C. Variation al Auto encoders
C. 变分自编码器
Variation al Auto encoders (VAEs) [20] are a very popular class of deep generative models, which consist of a simple latent variable and a neural network which transforms its value into the parameters of a simple likelihood function. The neural network parameters are optimized by gradient ascent on the variation al objective called the evidence lower bound (ELBO), which approximates maximum likelihood learning. To extend this model to a sequential setting, we employ variation al recurrent neural networks (VRNNs) [21]. In our setting, we have additional context provided as input to those models, so they are technically conditional, that is CVAEs and CVRNNs respectively.
变分自编码器 (VAE) [20] 是一类非常流行的深度生成模型,它由一个简单的潜变量和一个神经网络组成,该网络将其值转换为简单似然函数的参数。神经网络参数通过梯度上升法优化变分目标(即证据下界 (ELBO) ),该目标近似于最大似然学习。为了将该模型扩展到序列场景,我们采用了变分循环神经网络 (VRNN) [21]。在我们的设定中,这些模型还有额外的上下文作为输入,因此从技术上讲它们是条件模型,即分别为条件变分自编码器 (CVAE) 和条件变分循环神经网络 (CVRNN)。
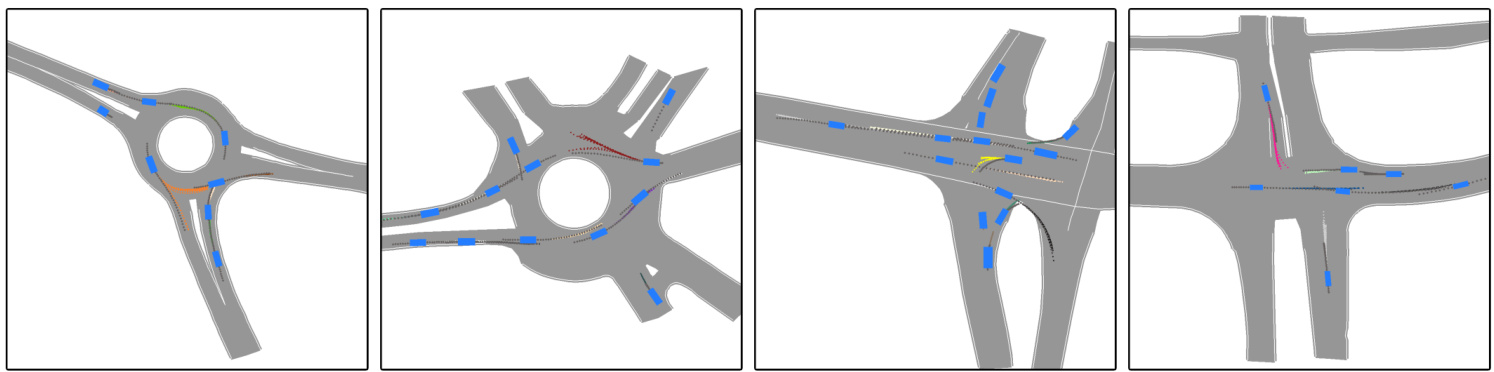
Fig. 1: Example predictions of ITRA for 3 seconds into the future based on a 1 second history. In most cases, the model is able to predict the ground truth trajectory with near certainty, but sometimes, such as when approaching a roundabout exit, there is inherent uncertainty which gives rise to multi-modal predictions. The ground truth trajectory is plotted in dark gray.
图 1: ITRA基于1秒历史数据对未来3秒的预测示例。在多数情况下,该模型能以近乎确定的概率预测真实轨迹,但在某些场景(如接近环岛出口时)会因固有不确定性产生多模态预测。真实轨迹以深灰色标出。
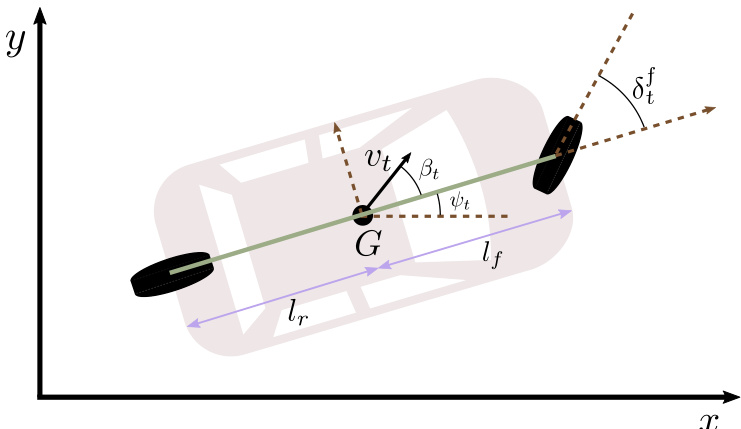
Fig. 2: [19] The kinematic bicycle model. $G$ is the geometric center of the vehicle and $v_{t}$ is its instantaneous velocity. Since our dataset does not contain entries for $\delta_{t}^{f}$ , we regard $\beta_{t}$ as steering directly, which is mathematically equivalent to setting $l_{f}=0$ . We fit $l_{r}$ by grid search for each recorded vehicle trajectory.
图 2: [19] 运动学自行车模型。$G$ 表示车辆的几何中心,$v_{t}$ 为其瞬时速度。由于数据集中未包含 $\delta_{t}^{f}$ 的条目,我们将 $\beta_{t}$ 直接视为转向角,这在数学上等价于设定 $l_{f}=0$。我们通过网格搜索为每条记录的车辆轨迹拟合 $l_{r}$ 值。
III. METHOD
III. 方法
Our model consists of a map specifying the driveable area and a composition of homogeneous agents, whose interactions are mediated by a differentiable simulator. At each timestep $t$ , each agent $i$ chooses an action $a_{t}^{i}$ , which then determines its next state according to a kinematic model $s_{t+1}^{i}~=~k i n(s_{t}^{i},a_{t}^{i})$ , which is usually the bicycle model, but we also explore some alternatives in Section IV-C. The states of all agents are pooled together to form the full state of the world $s_{t}$ , which is presented to each agent as $b_{t}^{i}$ , a rasterized, ego-centered and ego-rotated birdview image, as depicted in Figure 3. This rasterized birdview representation is commonly employed in existing models [22], [8], [11]. We choose to use three RGB channels to reduce the embedding network size. Each agent has its own hidden state $h_{t}^{i}$ , which serves as the agent’s memory, and a source of randomness ${\boldsymbol{z}}_{t}^{i}$ , which is a random variable that is used to generate the agent’s stochastic behavior. The full generative model then factorizes as follows
我们的模型包含一个指定可行驶区域的地图和一组同质智能体 (agent) ,这些智能体之间的交互通过可微分模拟器进行协调。在每个时间步 $t$ ,每个智能体 $i$ 选择一个动作 $a_{t}^{i}$ ,随后根据运动学模型 $s_{t+1}^{i}~=~k i n(s_{t}^{i},a_{t}^{i})$ 确定其下一状态——通常采用自行车模型,但我们也在第 IV-C 节探讨了其他替代方案。所有智能体的状态汇集形成全局世界状态 $s_{t}$ ,并以栅格化、自我中心且随自身旋转的鸟瞰图像 $b_{t}^{i}$ 形式呈现给每个智能体,如图 3 所示。这种栅格化鸟瞰表示法在现有模型 [22][8][11] 中被广泛采用。我们选择使用三个 RGB 通道以减少嵌入网络规模。每个智能体拥有专属的隐藏状态 $h_{t}^{i}$ 作为记忆单元,以及随机源 ${\boldsymbol{z}}_{t}^{i}$ ——该随机变量用于生成智能体的随机行为。完整的生成模型可分解如下:
$$
\begin{array}{l l}{{}}&{{(1)=\qquad\quad}}\ {{}}&{{\displaystyle\int\int\prod_{t=1}^{T}\prod_{i=1}^{N}p(z_{t}^{i})p(a_{t}^{i}|b_{t}^{i},z_{t}^{i},h_{t}^{i})p(s_{t+1}^{i}|s_{t}^{i},a_{t}^{i})d z_{1:T}^{1:N}d a_{1:T}^{1:N}}}\end{array}
$$
$$
\begin{array}{l l}{{}}&{{(1)=\qquad\quad}}\ {{}}&{{\displaystyle\int\int\prod_{t=1}^{T}\prod_{i=1}^{N}p(z_{t}^{i})p(a_{t}^{i}|b_{t}^{i},z_{t}^{i},h_{t}^{i})p(s_{t+1}^{i}|s_{t}^{i},a_{t}^{i})d z_{1:T}^{1:N}d a_{1:T}^{1:N}}}\end{array}
$$
Our model uses additional information about the environment in a form of a map rendered onto the birdview image, but for clarity we omit this from our notation.
我们的模型使用了以鸟瞰图形式渲染的环境地图作为额外信息,但为了清晰起见,我们在表示法中省略了这部分。
In ITRA, the conditional distribution of actions given latent variables and observations $p(a_{t}^{i}|b_{t}^{i},z_{t}^{i},h_{t}^{i})$ is deterministic, the distribution of the latent variables is unit Gaussian $p(z_{t}^{i})=\mathcal{N}(0,1)$ , and the distribution of states is Gaussian with a mean dictated by the kinematic model and a fixed diagonal variance $p(s_{t+1}^{i}|s_{t}^{i},a_{t}^{i})=\mathcal{N}(k i n(s_{t}^{i},a_{t}^{i}),\sigma\mathbf{I})$ , where $\sigma$ is a hyper parameter of the model.
在ITRA中,给定潜在变量和观测值的动作条件分布 $p(a_{t}^{i}|b_{t}^{i},z_{t}^{i},h_{t}^{i})$ 是确定性的,潜在变量的分布为单位高斯分布 $p(z_{t}^{i})=\mathcal{N}(0,1)$,状态分布则是高斯分布,其均值由运动学模型决定,方差为固定对角矩阵 $p(s_{t+1}^{i}|s_{t}^{i},a_{t}^{i})=\mathcal{N}(kin(s_{t}^{i},a_{t}^{i}),\sigma\mathbf{I})$,其中 $\sigma$ 是模型的超参数。
A. Differentiable Simulation
A. 可微分模拟
While the essential modeling of human behavior is performed by the VRNN generating actions, an integral part of ITRA is embedding that VRNN in a simulation consisting of the kinematic model and the procedure for generating birdview images, which is used both at training and test time. The entire model is end-to-end differentiable, allowing the parameters of the VRNN to be trained by gradient descent. For the kinematic model, this is as simple as implementing its equations of motion in PyTorch [23], but the birdview image construction is more involved.
虽然人类行为的基本建模由生成动作的VRNN完成,但ITRA的关键部分是将该VRNN嵌入到包含运动学模型和鸟瞰图生成流程的仿真系统中,这套系统在训练和测试阶段都会使用。整个模型采用端到端可微分设计,使得VRNN参数能够通过梯度下降法进行训练。对于运动学模型而言,只需在PyTorch语言[23]中实现其运动方程即可,但鸟瞰图构建过程则更为复杂。
We use PyTorch3D [24], a PyTorch-based library for differentiable rendering, to construct the birdview images. While the library primarily targets 3D applications, we obtain a simple 2D raster iz ation by applying an orthographic projection camera and a minimal shader that ignores lighting.
我们使用基于PyTorch语言的可微分渲染库PyTorch3D [24]来构建鸟瞰图。虽然该库主要面向3D应用,但通过应用正交投影相机和忽略光照的最小着色器,我们实现了简单的2D光栅化。
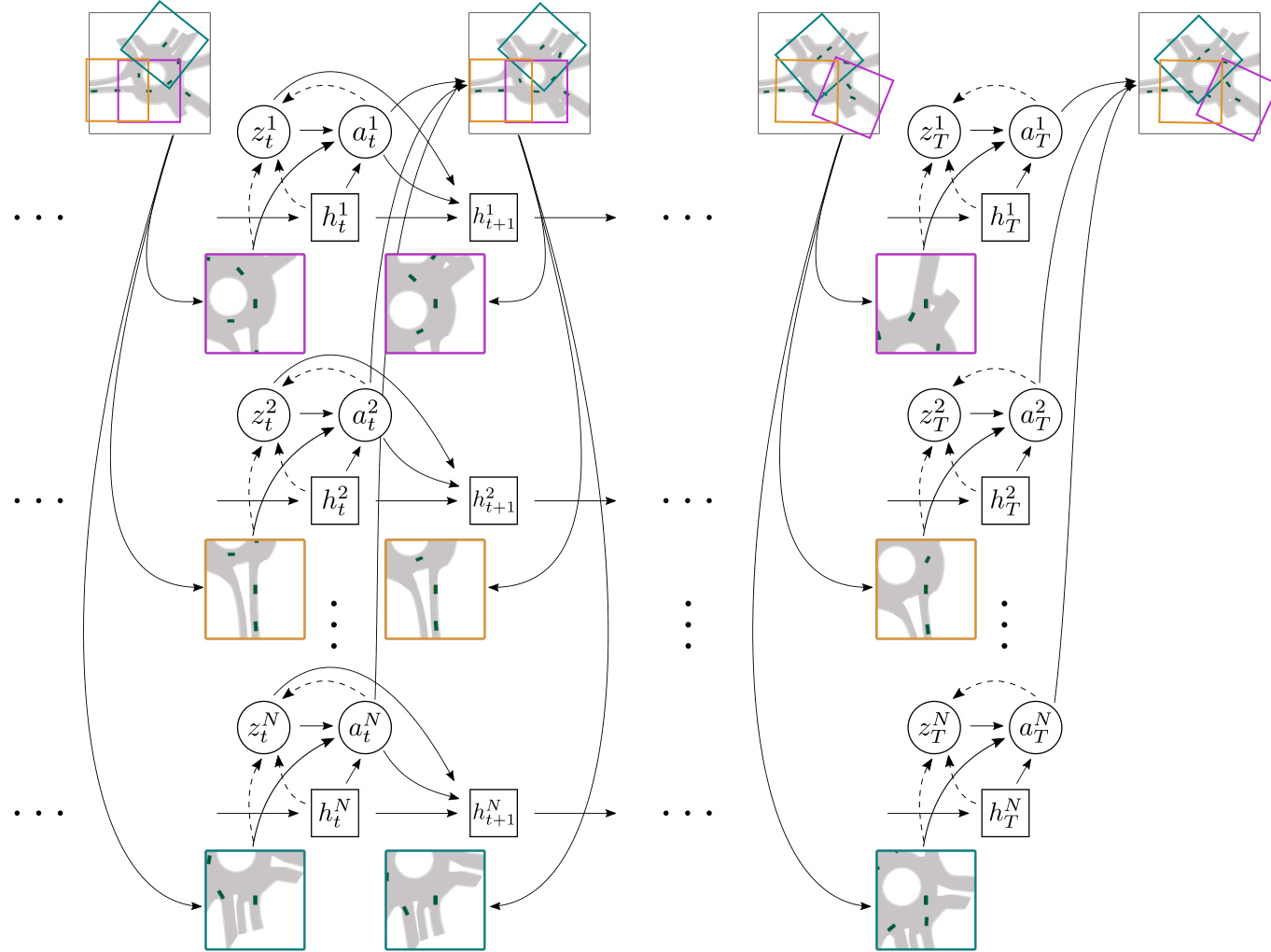
Fig. 3: A schematic illustration of ITRA’s architecture. The agents choose the actions at each time step independently from each other, obtaining information about other agents and the environment only through ego-centered birdview images. This representation naturally accommodates an unbounded, variable number of agents and time steps. The actions are translated into new agent states using a kinematic model not shown on the diagram. The colored bounding boxes illustrate each agent’s field of view in the full scene.
图 3: ITRA架构示意图。各AI智能体在每个时间步独立选择动作,仅通过以自我为中心的鸟瞰图像获取其他智能体及环境信息。这种表示方式天然支持无边界、可变数量的智能体与时间步。动作通过图中未展示的运动学模型转换为新的智能体状态。彩色边界框展示了各智能体在全场景中的视野范围。
To make the process differentiable we use the soft RGB blend algorithm [25].
为了使过程可微分,我们使用了软RGB混合算法 [25]。
B. Neural Networks
B. 神经网络
Each agent is modelled with a two-layer recurrent neural network using the gated recurrent unit (GRU) with a convolutional neural network (CNN) encoder for processing the birdview image. The remaining components are fully connected. We choose the latent dimensions to be 64 for $h$ and 2 for $z$ and we use birdview images in $256\times256$ resolution corresponding to a $100\times100$ meter area. We chose standard, well-established architectures to demonstrate that the improved performance in ITRA comes from the inclusion of a differentiable simulator.
每个智能体采用双层循环神经网络建模,使用门控循环单元 (GRU) 和卷积神经网络 (CNN) 编码器处理鸟瞰图像,其余组件为全连接结构。我们设定潜在维度为:$h$ 取64,$z$ 取2,并使用对应 $100\times100$ 米区域的 $256\times256$ 分辨率鸟瞰图像。选择这些标准成熟架构是为了证明ITRA的性能提升源于可微分模拟器的引入。
as the ground truth action extracted from the data, defining a variation al distribution $q(z_{t}^{i}|a_{t}^{i},b_{t}^{i},h_{t}^{i})$ . The ELBO is then defined as
将数据中提取的真实动作作为基础,定义一个变分分布 $q(z_{t}^{i}|a_{t}^{i},b_{t}^{i},h_{t}^{i})$ 。随后定义ELBO为
$$
\begin{array}{r}{\mathcal{L}=\displaystyle\sum_{i=1}^{N}\sum_{t=1}^{T-1}\bigg(\mathbb{E}{q(z_{t}^{i}|a_{t}^{i},b_{t}^{i},h_{t}^{i})}\left[\log p(s_{t+1}^{i}|b_{t}^{i},z_{t}^{i},h_{t}^{i})\right]}\ {-K L\left[q(z_{t}^{i}|a_{t}^{i},b_{t}^{i},h_{t}^{i})||p(z_{t}^{i})\right]\bigg),}\end{array}
$$
$$
\begin{array}{r}{\mathcal{L}=\displaystyle\sum_{i=1}^{N}\sum_{t=1}^{T-1}\bigg(\mathbb{E}{q(z_{t}^{i}|a_{t}^{i},b_{t}^{i},h_{t}^{i})}\left[\log p(s_{t+1}^{i}|b_{t}^{i},z_{t}^{i},h_{t}^{i})\right]}\ {-K L\left[q(z_{t}^{i}|a_{t}^{i},b_{t}^{i},h_{t}^{i})||p(z_{t}^{i})\right]\bigg),}\end{array}
$$
where $s_{t}^{i}$ are the ground truth states obtained from the dataset. This is the standard setting for training conditional variation al recurrent neural networks (CVRNNs), with a caveat that we introduce a distinction between actions and states.
其中 $s_{t}^{i}$ 是从数据集中获取的真实状态。这是训练条件变分循环神经网络 (CVRNN) 的标准设置,但需要注意我们引入了动作和状态之间的区分。
C. Training and Losses
C. 训练与损失
We train all the network components jointly from scratch using the evidence lower bound (ELBO) as the optimization objective. For this purpose, we use an inference network that parameter ize s a diagonal Gaussian distribution over $z$ given the current observation and recurrent state, as well
我们使用证据下界(ELBO)作为优化目标,从头开始联合训练所有网络组件。为此,我们采用了一个推理网络,该网络基于当前观测值和循环状态对$z$进行对角高斯分布的参数化。
D. Conditional Predictions
D. 条件预测
Typically, trajectory prediction tasks are defined as predicting a future trajectory $T_{o b s}+1:T$ based on a past trajectory $1:T_{o b s}$ . Predicting trajectories from a single frame is unnecessarily difficult and using Eq. 2 naively with a randomly initialized recurrent state $h_{1}$ destabilize s the training process and leads to poor predictions. To make sure the recurrent state is seeded well, we employ teacher forcing for states $s_{t}$ at time $1:T_{o b s}$ but not after $T_{o b s}$ , which corresponds to performing an inference over the state of $h_{T_{o b s}}$ given observations from previous time steps. We do this both at training and test time.
通常,轨迹预测任务被定义为根据过去轨迹 $1:T_{obs}$ 预测未来轨迹 $T_{obs}+1:T$。从单帧预测轨迹会不必要地增加难度,若直接使用公式2并随机初始化循环状态 $h_1$,会导致训练过程不稳定并产生较差预测结果。为确保循环状态良好初始化,我们对 $1:T_{obs}$ 时段的状态 $s_t$ 采用教师强制策略,但在 $T_{obs}$ 之后不使用。这相当于基于先前时间步的观测值对 $h_{T_{obs}}$ 状态进行推断。该策略在训练和测试阶段均被采用。
IV. EXPERIMENTAL RESULTS
IV. 实验结果
For our experiments, we use the INTERACTION dataset [16], which consists of about 10 hours of traffic data containing 36,000 vehicles recorded in 11 locations around the world at intersections, roundabouts, and highway ramps. Our model achieves state-of-the-art performance, as reported in Table I, and we also provide in Table II a more detailed breakdown of the scores it achieves across different scenes to enable a more fine-grained analysis. Finally, we ablate the kinematic bicycle model and the birdview generation for future times, the two key components of ITRA’s simulation, showing that both of them are necessary to achieve the reported performance.
在我们的实验中,我们使用了INTERACTION数据集[16],该数据集包含约10小时的交通数据,记录了全球11个地点(包括交叉路口、环岛和高速公路匝道)的36,000辆车辆。如表I所示,我们的模型实现了最先进的性能,并在表II中提供了更详细的分数细分,以便进行更细粒度的分析。最后,我们对ITRA仿真中的两个关键组件(运动学自行车模型和未来时间的鸟瞰图生成)进行了消融实验,结果表明两者对于实现所报告的性能都是必要的。
Following the recommendation of [11], we apply classmates forcing, where the actions and states of all agents other than the ego vehicle are fixed to ground truth at training time and not generated by the VRNN, which allows us to use batches of diverse examples and stabilizes training. At test time, we predict the motion of all agents in the scene, including bicycles/pedestrians (which are not distinguished from each other in the dataset). For simplicity, we use the same model trained on vehicles to predict all agent types, noting that it could be possible to obtain further improvements by training a separate model for bicycles/pedestrians. We trained all the model components jointly from scratch using the ADAM optimizer [26] with the standard learning rate of 3e-4, using gradient clipping and a batch size of 8. We found the training to be relatively stable with respect to other hyper parameters and have not performed extensive tuning. The training process takes about two weeks on a single NVIDIA Tesla P100 GPU.
遵循[11]的建议,我们采用同学强制(classmates forcing)策略:在训练时将非自车(non-ego vehicle)的所有智能体动作和状态固定为真实值而非由VRNN生成,这使我们能使用多样化样本批次并稳定训练。测试时,我们预测场景中所有智能体(包括自行车/行人,该数据集未对二者区分)的运动。为简化流程,我们使用同一套针对车辆训练的模型预测所有智能体类型,但指出通过为自行车/行人单独训练模型可能获得进一步改进。我们使用ADAM优化器[26]以3e-4标准学习率从头联合训练所有模型组件,采用梯度裁剪和批次大小为8的配置。训练过程对其他超参数相对稳定,未进行大量调参。在单块NVIDIA Tesla P100 GPU上训练耗时约两周。
Finally, we note that we compute ground truth actions used as input to the inference network based on a sequence of ground truth states, independently of what the model predicts at earlier times. We found that this greatly speeds up training and leads to better final performance.
最后,我们注意到,我们基于一系列真实状态计算作为推理网络输入的真实动作,而不依赖于模型在早期时间点的预测。我们发现这能显著加快训练速度并带来更好的最终性能。
A. Evaluation Metrics
A. 评估指标
where $(x_{t}^{i},y_{t}^{i})$ is the ground truth position of agent $i$ at time $t$ . When multiple trajectory predictions can be generated,
其中 $(x_{t}^{i},y_{t}^{i})$ 是智能体 $i$ 在时间 $t$ 的真实位置。当可以生成多个轨迹预测时,
TABLE I: Validation set prediction errors on the INTERACTION Dataset evaluated with the suggested train/validation split. The evaluation is based on six samples, where for each example the trajectory with the smallest error is selected, independently for ADE and FDE. ReCoG only makes deterministic predictions, so its performance would be the same with a single sample. The values for baselines are as reported by their original authors, with the exception of DESIRE and MultiPath, where we present the results reported in [9].
表 1: 基于建议的训练/验证划分在INTERACTION数据集上验证集的预测误差评估。该评估基于六个样本,其中每个样本独立选取ADE和FDE误差最小的轨迹。ReCoG仅进行确定性预测,因此其单样本性能保持不变。基线数据来源于原作者报告,但DESIRE和MultiPath的结果采用[9]中报告的数据。
| 方法 | minADE6 | min FDE6 |
|---|---|---|
| DESIRE [5] | 0.32 | 0.88 |
| MultiPath [3] | 0.30 | 0.99 |
| TNT [9] | 0.21 | 0.67 |
| ReCoG [17] | 0.19 | 0.65 |
| ITRA (ours) | 0.17 | 0.49 |
TABLE II: Breakdown of ITRA’s performance across individual scenes in the INTERACTION dataset. We present evaluation of a single model trained on all scenes jointly, noting that fine-tuning on individual scenes can further improve performance. CHN Merging ZS, which is a congested highway where predictions are relatively easy, is overrepresented in the dataset, lowering the average error across scenes.
表 II: ITRA 在 INTERACTION 数据集中各场景的性能细分。我们展示了在所有场景上联合训练的单一模型评估结果,并指出针对单个场景进行微调可以进一步提升性能。CHN Merging ZS 是一条拥堵的高速公路场景,其预测相对容易,但该场景在数据集中占比过高,从而拉低了跨场景的平均误差。
| 场景 | minADE6 | min FDE6 | MFD6 |
|---|---|---|---|
| CHN Merging ZS | 0.127 | 0.356 | 2.157 |
| CHN RoundaboutLN | 0.199 | 0.549 | 2.354 |
| DEUI Merging MT | 0.226 | 0.678 | 2.178 |
| DEURoundaboutOF | 0.283 | 0.766 | 3.389 |
| USAIntersectionEPO | 0.215 | 0.640 | 3.008 |
| USAIntersectionEP1 | 0.234 | 0.678 | 2.974 |
| USAIntersection GL | 0.203 | 0.611 | 2.750 |
| USAIntersectionMA | 0.212 | 0.634 | 3.430 |
| USARoundaboutEP | 0.234 | 0.690 | 3.094 |
| USARoundaboutFT | 0.219 | 0.661 | 2.932 |
| USARoundaboutSR | 0.178 | 0.525 | 2.451 |
the predicted trajectory with the smallest error is selected for evaluation. In either case, the errors are averaged across agents and test examples.
选择误差最小的预测轨迹进行评估。无论哪种情况,误差都会在智能体和测试样本间取平均值。
$$
\begin{array}{l}{\displaystyle\operatorname*{min}\mathrm{ADE}{K}=\frac{1}{N}\sum_{i=1}^{N}\operatorname*{min}{k}\mathrm{ADE}{k}^{i}}\ {\displaystyle\operatorname*{min}\mathrm{FDE}{K}=\frac{1}{N}\sum_{i=1}^{N}\operatorname*{min}{k}\mathrm{FDE}_{k}^{i}}\end{array}
$$
$$
\begin{array}{l}{\displaystyle\operatorname*{min}\mathrm{ADE}{K}=\frac{1}{N}\sum_{i=1}^{N}\operatorname*{min}{k}\mathrm{ADE}{k}^{i}}\ {\displaystyle\operatorname*{min}\mathrm{FDE}{K}=\frac{1}{N}\sum_{i=1}^{N}\operatorname*{min}{k}\mathrm{FDE}_{k}^{i}}\end{array}
$$
Note that these metrics only score position and not orientation or speed predictions, so most trajectory prediction models only generate position coordinates.
请注意,这些指标仅评估位置预测,而不涉及方向或速度预测,因此大多数轨迹预测模型仅生成位置坐标。
While not directly measuring performance, a useful metric for tracking the diversity of predicted trajectories is the Maximum Final Distance (MFD)
虽然不直接衡量性能,但最大终点距离 (MFD) 是追踪预测轨迹多样性的有效指标
$$
\mathrm{MFD}{K}=\frac{1}{N}\sum_{i=1}^{N}\operatorname*{max}{k,l}\sqrt{(x_{T}^{i,k}-x_{T}^{i,l})^{2}+(y_{T}^{i,k}-y_{T}^{i,l})^{2}},
$$
$$
\mathrm{MFD}{K}=\frac{1}{N}\sum_{i=1}^{N}\operatorname*{max}{k,l}\sqrt{(x_{T}^{i,k}-x_{T}^{i,l})^{2}+(y_{T}^{i,k}-y_{T}^{i,l})^{2}},
$$
which we primarily use to diagnose when the model collapses onto deterministic predictions.
我们主要用它来诊断模型何时坍缩为确定性预测。
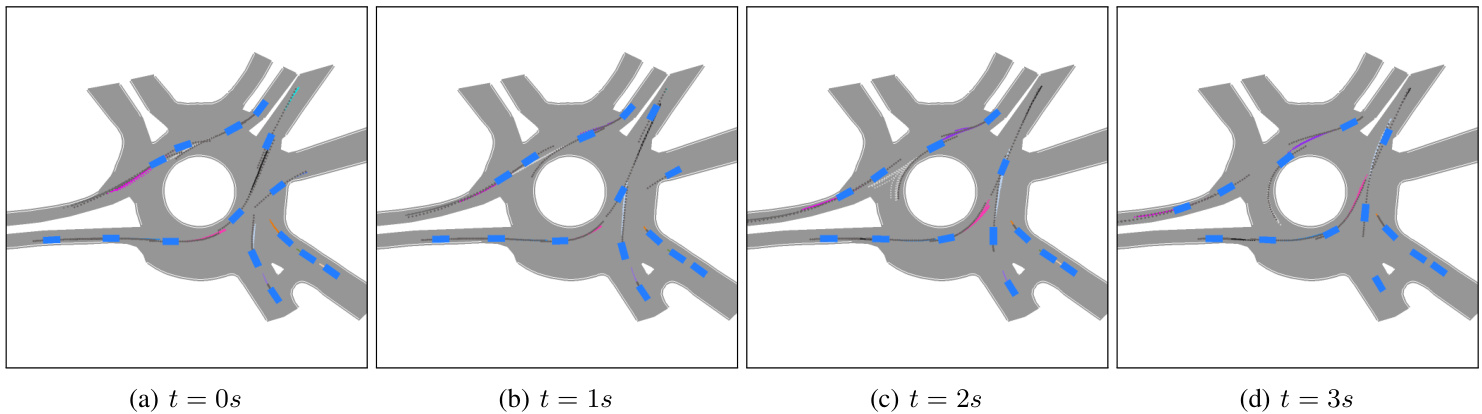
Fig. 4: A sequence of 4 subsequent prediction snapshots spaced 1 second apart. For each vehicle in the scene we show 10 sampled predictions over the subsequent 3 seconds based on the previous 1 second. Notice the car that just entered the roundabout from top-right in 4a, for which ITRA predicts that it will go forward in the roundabout, and as it enters the roundabout in $_{\mathrm{4c}}$ , the prediction diversifies to include both exiting the roundabout and continuing the turn, finally matching the ground truth trajectory (in dark grey) in 4d once the car started turning.
图 4: 间隔1秒的连续4个预测快照序列。针对场景中每辆车,我们基于前1秒数据展示了未来3秒内的10条采样预测轨迹。注意4a中刚从右上角进入环岛的车辆:ITRA最初预测其将直行通过环岛,当车辆进入环岛时(4c),预测轨迹开始分化出"驶离环岛"和"继续转弯"两种可能,最终在车辆开始转弯时(4d)与真实轨迹(深灰色)完全吻合。
B. Ablations on Future Birdview Images
B. 未来鸟瞰图像的消融实验
A key aspect of ITRA is the ongoing simulation throughout the future time
