Synthesizer: Rethinking Self-Attention for Transformer Models
Synthesizer: 重新思考Transformer模型中的自注意力机制
Yi Tay 1 Dara Bahri 1 Donald Metzler 1 Da-Cheng Juan 1 Zhe Zhao 1 Che Zheng
Yi Tay 1 Dara Bahri 1 Donald Metzler 1 Da-Cheng Juan 1 Zhe Zhao 1 Che Zheng
Abstract
摘要
The dot product self-attention is known to be central and indispensable to state-of-the-art Transformer models. But is it really required? This paper investigates the true importance and contribution of the dot product-based self-attention mechanism on the performance of Transformer models. Via extensive experiments, we find that (1) random alignment matrices surprisingly perform quite competitively and (2) learning attention weights from token-token (query-key) in- teractions is useful but not that important after all. To this end, we propose SYNTHESIZER, a model that learns synthetic attention weights without token-token interactions. In our experiments, we first show that simple Synthesizers achieve highly competitive performance when compared against vanilla Transformer models across a range of tasks, including machine translation, language modeling, text generation and GLUE/SuperGLUE benchmarks. When composed with dot product attention, we find that Synthesizers consistently outperform Transformers. Moreover, we conduct additional comparisons of Synthesizers against Dynamic Convolutions, showing that simple Random Synthesizer is not only $60%$ faster but also improves perplexity by a relative $3.5%$ . Finally, we show that simple factorized Synthesizers can outperform Linformers on encoding only tasks.
点积自注意力 (dot product self-attention) 机制被认为是当前最先进 Transformer 模型的核心且不可或缺的组成部分。但它真的必不可少吗?本文研究了基于点积的自注意力机制对 Transformer 模型性能的实际重要性和贡献。通过大量实验,我们发现:(1) 随机对齐矩阵的表现出人意料地具有竞争力;(2) 从 token-token (query-key) 交互中学习注意力权重虽然有用,但最终并不那么重要。为此,我们提出了 SYNTHESIZER——一种无需 token-token 交互即可学习合成注意力权重的模型。在实验中,我们首先证明:与原始 Transformer 模型相比,简单的 Synthesizer 在机器翻译、语言建模、文本生成以及 GLUE/SuperGLUE 基准测试等一系列任务中均能实现极具竞争力的性能。当与点积注意力结合使用时,Synthesizer 始终优于 Transformer。此外,我们将 Synthesizer 与动态卷积 (Dynamic Convolutions) 进行对比,结果表明简单的随机 Synthesizer 不仅速度快 60%,还能将困惑度相对降低 3.5%。最后,我们证明在纯编码任务中,简单的因子分解 Synthesizer 可以超越 Linformer。
1. introduction
1. 引言
Transformer models (Vaswani et al., 2017) have demonstrated success across a wide range of tasks. This has resulted in Transformers largely displacing once popular auto-regressive and recurrent models in recent years. At the heart of Transformer models lies the query-key-value dot product attention. The success of Transformer models is widely attributed to this self-attention mechanism since fully connected token graphs, which are able to model long-range dependencies, provide a robust inductive bias.
Transformer模型 (Vaswani等人, 2017) 已在广泛任务中展现出卓越性能。近年来,Transformer已基本取代曾风靡一时的自回归模型和循环模型。该模型的核心在于查询-键-值点积注意力机制 (query-key-value dot product attention) 。Transformer的成功普遍归功于这种自注意力机制——通过构建全连接的token关系图来建模长程依赖关系,从而形成强大的归纳偏置。
But is the dot product self-attention really so important? Do we need it? Is it necessary to learn attention weights via pairwise dot products? This paper seeks to develop a deeper understanding of the role that the dot product self-attention mechanism plays in Transformer models.
但点积自注意力真的如此重要吗?我们是否需要它?是否必须通过成对点积来学习注意力权重?本文旨在深入理解点积自注意力机制在Transformer模型中的作用。
The fundamental role of dot product self-attention is to learn self-alignment, i.e., to determine the relative importance of a single token with respect to all other tokens in the sequence. To this end, there have been memory metaphors and analogies constructed to support this claim. Indeed, the terms query, keys, and values imply that self-attention emulates a content-based retrieval process which leverages pairwise interactions at its very core.
点积自注意力 (self-attention) 的基本作用是学习自对齐 (self-alignment),即确定序列中单个 token 相对于所有其他 token 的相对重要性。为此,人们构建了记忆隐喻和类比来支持这一观点。实际上,术语 query、key 和 value 暗示自注意力模拟了一个基于内容的检索过程,其核心利用了成对交互。
Moving against convention, this paper postulates that we cannot only do without dot product self-attention but also content-based memory-like self-attention altogether. Traditionally, attention weights are learned at the instance or sample level, where weights are produced by instance-level pairwise interactions. As a result, these instance-specific interactions often fluctuate freely across different instances as they lack a consistent global context.
与传统观点相反,本文提出我们不仅可以摒弃点积自注意力 (dot product self-attention) ,还能完全舍弃基于内容的类记忆自注意力机制。传统方法通常在实例或样本级别学习注意力权重,这些权重通过实例间的成对交互产生。因此,由于缺乏一致的全局上下文,这些特定于实例的交互往往在不同实例间自由波动。
This paper proposes SYNTHESIZER, a new model that learns to synthesize the self-alignment matrix instead of manually computing pairwise dot products. We propose a diverse suite of synthesizing functions and extensively evaluate them. We characterize the source information that these synthesizing functions receive, i.e., whether they receive information from individual tokens, token-token interactions, and/or global task information. Intuitively, different source inputs to the synthesizing functions should capture diverse views, which may be useful when employed in conjunction.
本文提出SYNTHESIZER,这是一种学习合成自对齐矩阵而非手动计算成对点积的新模型。我们提出了一套多样化的合成函数并进行了广泛评估。我们分析了这些合成函数接收的源信息类型,即它们是否接收来自单个token、token间交互和/或全局任务信息。直观来看,合成函数的不同输入源应能捕捉多样化视角,这些视角在联合使用时可能具有价值。
Aside from generalizing the standard Transformer model, we show that it is possible to achieve competitive results with fully global attention weights that do not consider token-token interactions or any instance-level (local) information at all. More specifically, a random matrix SYNTHESIZER model achieves a 27.27 BLEU score on WMT 2014
除了对标准Transformer模型进行泛化外,我们还表明,完全无需考虑token间交互或任何实例级(局部)信息的全局注意力权重也能取得具有竞争力的结果。具体而言,一个随机矩阵SYNTHESIZER模型在WMT 2014上取得了27.27的BLEU分数。
English-German1. Via a set of rigorous experiments, we observe that the popular and well-established dot-product content-based attention can be approximated with simpler variants such as random matrices or dense layers without sacrificing much performance in some cases.
英德1. 通过一系列严格实验,我们观察到在某些情况下,流行且成熟的点积基于内容的注意力机制可以用更简单的变体(如随机矩阵或全连接层)近似替代,而不会显著损失性能。
In our experiments, we also show that our relatively simple Synthesizer models also outperform Dynamic Convolutions (Wu et al., 2019) with a $+3.5%$ relative improvement in perplexity while being $60%$ faster. On encoding tasks, our factorized Synthesizers can outperform other low-rank efficient Transformer models such as Linformers (Wang et al., 2020).
在我们的实验中,我们还展示了相对简单的Synthesizer模型也优于动态卷积 (Dynamic Convolutions) (Wu et al., 2019) ,困惑度相对提升了 +3.5% ,同时速度快了 60% 。在编码任务中,我们的因子化Synthesizer可以超越其他低秩高效的Transformer模型,例如Linformer (Wang et al., 2020) 。
While simple Synthesizer models are able to perform competitively, our experiments show that the pairwise dot product is still ultimately helpful. When composing our synthesizing functions with dot products, we find that they consistently improve the performance of Transformers. In general, we believe our findings will spur further investigation and discussion about the true role and utility of the self-attention mechanism in Transformer models.
虽然简单的合成器(Synthesizer)模型能够表现出竞争力,但我们的实验表明点积运算最终仍具有实际帮助。当将合成函数与点积运算结合时,我们发现它们能持续提升Transformer模型的性能。总体而言,我们相信这些发现将推动关于Transformer模型中自注意力机制真实作用和效用的进一步研究与探讨。
Our Contributions Our key contributions are described as follows:
我们的贡献
我们的主要贡献如下:
2. Related Work
2. 相关工作
Attention-based models are used across a wide spectrum of problem domains. Such models are especially popular, due to their effectiveness, in the language and vision domains. Attention models can be traced back to the machine translation models of (Bahdanau et al., 2014) and (Luong et al., 2015), where attention is employed to learn soft word alignments between language pairs. The intuition behind the attention mechanism is deeply-rooted in the notion of memory-based retrieval (Graves et al., 2014; Weston et al., 2014), in which soft differentiable addressing of memory was initially proposed.
基于注意力(Attention)的模型被广泛应用于各类问题领域。这类模型因其高效性在语言和视觉领域尤为流行。注意力模型可追溯至(Bahdanau et al., 2014)和(Luong et al., 2015)的机器翻译模型,其中采用注意力机制来学习语言对之间的软词对齐。注意力机制背后的直觉深植于基于记忆检索的概念(Graves et al., 2014; Weston et al., 2014),该概念最初提出了可微分软寻址内存的方法。
The paradigm of learning self-alignments, also known as self-attention, has been largely popularized by Transformer models (Vaswani et al., 2017). This technical narrative has also been explored by a number of other recent studies, including those on intra-attention (Parikh et al., 2016), self-matching networks (Wang et al., 2017), and LSTMN (Cheng et al., 2016). To this end, Transformer models, which function primarily based on self-attention and feedforward layers, generally serve as a reliable replacement for auto regressive recurrent models.
学习自对齐(self-attention)的范式主要由Transformer模型(Vaswani等人,2017)推广开来。这一技术路线也被近期多项研究探索过,包括内部注意力(intra-attention)(Parikh等人,2016)、自匹配网络(self-matching networks)(Wang等人,2017)以及LSTMN(Cheng等人,2016)。因此,主要基于自注意力和前馈层运作的Transformer模型,通常能可靠地替代自回归循环模型。
The self-attention layer itself has been the subject of many recent technical innovations. For example, recent studies have investigated improving the layer’s overall efficiency via spars if i cation and reducing the complexity of computing the alignment matrix (Child et al., 2019; Kitaev et al., 2020; Huang et al., 2018; Tay et al., 2020; Beltagy et al., 2020). These methods are tightly coupled with the query-key-value paradigm, employing a form of memory-based content retrieval as an attention mechanism. On the other end of the spectrum, there have been studies that advocate for replacing self-attention with convolution (Wu et al., 2019). The recent surge in interest in simplifying the attention mechanism raises important questions about the role and utility of the pairwise dot products, which are one the defining characteristics of self-attention models. Meanwhile, in the image domain, (Cordonnier et al., 2019) shows connection of Transformers with CNNs.
自注意力层本身已成为许多近期技术创新的研究对象。例如,近期研究探索了通过稀疏化 (sparsification) 和降低对齐矩阵计算复杂度来提升该层的整体效率 (Child et al., 2019; Kitaev et al., 2020; Huang et al., 2018; Tay et al., 2020; Beltagy et al., 2020)。这些方法与查询-键-值范式紧密耦合,采用基于记忆的内容检索形式作为注意力机制。另一方面,也有研究主张用卷积替代自注意力 (Wu et al., 2019)。近期简化注意力机制的研究热潮引发了对点积对作用的深刻思考——这一特性正是自注意力模型的核心特征之一。与此同时,在图像领域,(Cordonnier et al., 2019) 揭示了Transformer与CNN的关联性。
Our work is a new take on the self-attention mechanism in Transformer models. We delve deeper, starting with replacing the pairwise dot products with what we call synthesizing functions that learn attention matrices that may or may not depend on the input tokens. The most closely related work is ((Raganato et al., 2020)), in which the authors propose using fixed (i.e., not learned) attention patterns in Transformer encoders. However, the scope of their work is limited to encoders and relies on manually defined handcrafted patterns that seem to work well. Our work takes this intuition further and expands on this narrative.
我们对Transformer模型中的自注意力机制提出了新的见解。我们进行了更深入的探索,首先用所谓的合成函数替代了成对点积运算,这些函数可以学习到可能依赖也可能不依赖输入token的注意力矩阵。与之最相关的研究是 (Raganato et al., 2020) ,作者提出在Transformer编码器中使用固定(即非学习型)注意力模式。然而,他们的研究范围仅限于编码器,且依赖于人工定义的经验模式。我们的工作进一步发展了这一思路并拓展了其应用范畴。
MLP-Mixers are Random Synthesizers This is an update2 discussing the relationship between Random Synthesizers and recent MLP-Mixers (Tolstikhin et al., 2021). There have been recent work (April 2021) that proposed AllMLP architectures for vision. Although, this work made it’s appearance first in May 2020, a year before the MLP-Mixer was proposed, we show that Random Synthesizers are a form of MLP-Mixers. Random Synthesizers apply a weight matrix $R$ on the length dimension. $R$ is a $L\times L$ matrix and can be seen as a form of projection across the length dimension. This is equivalent to transposing the axis before linear projection in the token-mixer in the MLP-Mixer model. The key difference here is that (1) we use a softmax normalization on the kernel (weights) and (2) Random Synthesizers are a form of multi-headed MLP-Mixers.
MLP-Mixer是随机合成器
这是关于随机合成器与近期MLP-Mixer (Tolstikhin等人,2021) 关系的更新讨论。2021年4月有研究提出了面向视觉的AllMLP架构。尽管本工作最早出现于2020年5月 (比MLP-Mixer提出早一年),但我们证明随机合成器是MLP-Mixer的一种形式。随机合成器在长度维度上应用权重矩阵$R$。$R$是一个$L\times L$矩阵,可视为跨长度维度的投影形式。这等效于在MLP-Mixer模型的token混合器中进行线性投影前转置轴。关键区别在于:(1) 我们在核(权重)上使用softmax归一化;(2) 随机合成器是多头MLP-Mixer的一种形式。
3. The Proposed Method
3. 所提出的方法
This section introduces our proposed SYNTHESIZER model. At its core, our model is essentially a Transformer model with self-attention modules replaced with our Synthetic Attention modules. Figure 3.1 illustrates the key ideas behind (a) Transformer (b) Dense Synthesizers and (c) Random Synthesizers.
本节介绍我们提出的SYNTHESIZER模型。该模型本质上是一个用合成注意力模块(Synthetic Attention)取代自注意力模块的Transformer模型。图3.1展示了(a)Transformer、(b)密集合成器(Dense Synthesizer)和(c)随机合成器(Random Synthesizer)的核心思想。
3.1. Synthesizer Model
3.1. 合成器模型
This section introduces Synthetic Attention, our proposed self-attention module. Our model removes the notion of query-key-values in the self-attention module and directly synthesizes the alignment matrix instead. For simplicity, we describe the per head and per layer computation, which is denoted by $h$ and $\ell$ respectively in most cases.
本节介绍我们提出的合成注意力(Synthetic Attention)模块。该模型摒弃了自注意力(self-attention)模块中查询-键-值(query-key-value)的概念,直接合成对齐矩阵。为简化描述,我们以单头单层计算为例(在多数情况下分别用$h$和$\ell$表示)。
Dense Synthesizer Let us consider the simplest variation of the SYNTHESIZER model which is conditioned on each input token. Overall, our method accepts an input $X_{h,\ell}\in\mathbb{R}^{N\times d}$ and produces an output of $\bar{Y_{h,\ell}}\in\mathbb{R}^{\bar{N}\times d}$ Here, $\ell$ refers to the sequence length and $d$ refers to the dimens ional it y of the model. We first adopt $F_{h,\ell}(.)$ , a parameterized function, for projecting input $X_{i}$ from $d$ dimensions to $N$ dimensions.
密集合成器 (Dense Synthesizer)
让我们考虑SYNTHESIZER模型的最简单变体,该变体以每个输入token为条件。总体而言,我们的方法接受输入 $X_{h,\ell}\in\mathbb{R}^{N\times d}$ 并生成输出 $\bar{Y_{h,\ell}}\in\mathbb{R}^{\bar{N}\times d}$。其中 $\ell$ 表示序列长度,$d$ 表示模型的维度。我们首先采用参数化函数 $F_{h,\ell}(.)$ 将输入 $X_{i}$ 从 $d$ 维投影到 $N$ 维。
$$
B_{i,h,\ell}=F_{h,\ell}(X_{i,h,\ell})
$$
$$
B_{i,h,\ell}=F_{h,\ell}(X_{i,h,\ell})
$$
where $F_{h,\ell}(.)$ is a parameterized function that maps $\mathbb{R}^{d}$ to $\mathbb{R}^{\ell}$ and $i$ is the $i$ -th token of $X_{h,\ell}$ and is applied positionwise (to each vector in the sequence of length $N$ ). Intuitively, this can be interpreted as learning a token-wise projection to the sequence length $N$ . Essentially, with this model, each token predicts weights for each token in the input sequence. In practice, we adopt a simple two layered feed-forward layer with ReLU activation s for $F_{h,\ell}(.)$ :
其中 $F_{h,\ell}(.)$ 是一个将 $\mathbb{R}^{d}$ 映射到 $\mathbb{R}^{\ell}$ 的参数化函数,$i$ 表示 $X_{h,\ell}$ 的第 $i$ 个 token,该函数按位置作用于(长度为 $N$ 的序列中的每个向量)。直观上,这可以理解为学习一个面向序列长度 $N$ 的 token 级投影。本质上,该模型让每个 token 为输入序列中的每个 token 预测权重。实践中,我们采用简单的双层前馈网络(ReLU激活)来实现 $F_{h,\ell}(.)$:
$$
F_{h,\ell}(X_{i,h,\ell})=W_{2,h,\ell}(\sigma_{R}(W_{1,h,\ell}(X_{i,h,\ell}))
$$
$$
F_{h,\ell}(X_{i,h,\ell})=W_{2,h,\ell}(\sigma_{R}(W_{1,h,\ell}(X_{i,h,\ell}))
$$
where $\sigma_{R}$ is the ReLU activation function and $W_{1,h,\ell}\in$ $\mathbb{R}^{d\times d}$ and $W_{2,h,\ell}\in\mathbb{R}^{d\times\ell}$ . Hence, $B_{i,h,\ell}$ is now of $\mathbb{R}^{\ell}$ Given $B_{i,h,\ell}\in\mathbb{R}^{N\times N}$ , we now compute:
其中 $\sigma_{R}$ 是 ReLU 激活函数,$W_{1,h,\ell}\in$ $\mathbb{R}^{d\times d}$ 且 $W_{2,h,\ell}\in\mathbb{R}^{d\times\ell}$。因此,$B_{i,h,\ell}$ 现在是 $\mathbb{R}^{\ell}$ 的。给定 $B_{i,h,\ell}\in\mathbb{R}^{N\times N}$,我们现在计算:
$$
Y_{h,\ell}=\mathop{\mathrm{softmax}}(B_{h,\ell})G_{h,\ell}(X_{h,\ell})
$$
$$
Y_{h,\ell}=\mathop{\mathrm{softmax}}(B_{h,\ell})G_{h,\ell}(X_{h,\ell})
$$
where $G_{h,\ell}(.)$ is another parameterized function of $X$ that is analogous to $V_{h,\ell}$ (value) in the standard Transformer model. This approach eliminates the dot product attention $Y=$ $\mathrm{softmax}(Q_{h,\ell}K_{h,\ell}^{\top})V_{h,\ell}$ altogether by replacing $Q_{h,\ell}K_{h,\ell}^{\top}$ in standard Transformers with the synthesizing function $F_{h,\ell}(.)$ .
其中 $G_{h,\ell}(.)$ 是另一个关于 $X$ 的参数化函数,类似于标准Transformer模型中的 $V_{h,\ell}$ (value)。该方法通过用合成函数 $F_{h,\ell}(.)$ 替代标准Transformer中的 $Q_{h,\ell}K_{h,\ell}^{\top}$,彻底摒弃了点积注意力 $Y=$ $\mathrm{softmax}(Q_{h,\ell}K_{h,\ell}^{\top})V_{h,\ell}$。
Random Synthesizer The previous variant learns synthetic attention by conditioning on each input of $X$ and projecting to $N$ dimensions. Hence, the Dense Synthesizer conditions on each token independently, as opposed to pairwise token interactions in the vanilla Transformer model. We consider another variation of SYNTHESIZER where the attention weights are not conditioned on any input tokens. Instead, the attention weights are initialized to random values. These values can then either be trainable or kept fixed (denoted as Fixed).
随机合成器 (Random Synthesizer)
先前的变体通过以$X$的每个输入为条件并投影到$N$维来学习合成注意力。因此,密集合成器 (Dense Synthesizer) 独立地以每个token为条件,这与原始Transformer模型中的token对交互形成对比。我们考虑SYNTHESIZER的另一种变体,其中注意力权重不以任何输入token为条件。相反,注意力权重被初始化为随机值。这些值可以是可训练的,也可以保持固定 (表示为Fixed)。
Let $R_{h,\ell}$ be a randomly initialized matrix. The Random Synthesizer is defined as:
设 $R_{h,\ell}$ 为一个随机初始化的矩阵。随机合成器 (Random Synthesizer) 的定义如下:
$$
Y_{h,\ell}=\mathrm{softmax}(R_{h,\ell})G_{h,\ell}(X_{h,\ell}).
$$
$$
Y_{h,\ell}=\mathrm{softmax}(R_{h,\ell})G_{h,\ell}(X_{h,\ell}).
$$
where $R_{h,\ell}\in\mathbb{R}^{N\times N}$ . Notably, each head adds $N^{2}$ parameters to the network. The basic idea3 of the Random Synthesizer is to not rely on pairwise token interactions or any information from individual token but rather to learn a task-specific alignment that works well globally across many samples. This is a direct generalization of the recently proposed fixed self-attention patterns (Raganato et al., 2020).
其中 $R_{h,\ell}\in\mathbb{R}^{N\times N}$。值得注意的是,每个头会为网络增加 $N^{2}$ 个参数。Random Synthesizer 的核心思想3是不依赖token间的成对交互或单个token的信息,而是学习一种在多样本中全局有效的任务特定对齐方式。这直接推广了近期提出的固定自注意力模式 (Raganato et al., 2020) [20]。
Factorized Models The Dense Synthesizer adds $d\times N$ parameters to the network. On the other hand, the Random Synthesizer adds $N\times N$ parameters. Here, note that we omit the $Q,K$ projections in the standard Transformer which results in further parameter savings. Despite these savings, synthesized models can be cumbersome to learn when $\ell$ is large. Hence, we propose factorized variations of the SYNTHESIZER models and show that these variants perform comparably in practice.
因子化模型
Dense Synthesizer 为网络增加了 $d\times N$ 个参数,而 Random Synthesizer 则引入了 $N\times N$ 个参数。需要注意的是,我们省略了标准 Transformer 中的 $Q,K$ 投影,从而进一步节省了参数量。尽管如此,当 $\ell$ 较大时,合成模型的学习仍可能变得繁琐。因此,我们提出了 SYNTHESIZER 模型的因子化变体,并证明这些变体在实际应用中表现相当。
Factorized Dense Synthesizer Factorized outputs not only slightly reduce the parameter cost of the SYNTHE- SIZER but also aid in preventing over fitting. The factorized variant of the dense synthesizer can be expressed as follows:
分解式密集合成器
分解式输出不仅能略微降低合成器 (SYNTHESIZER) 的参数成本,还有助于防止过拟合。密集合成器的分解变体可表示为:
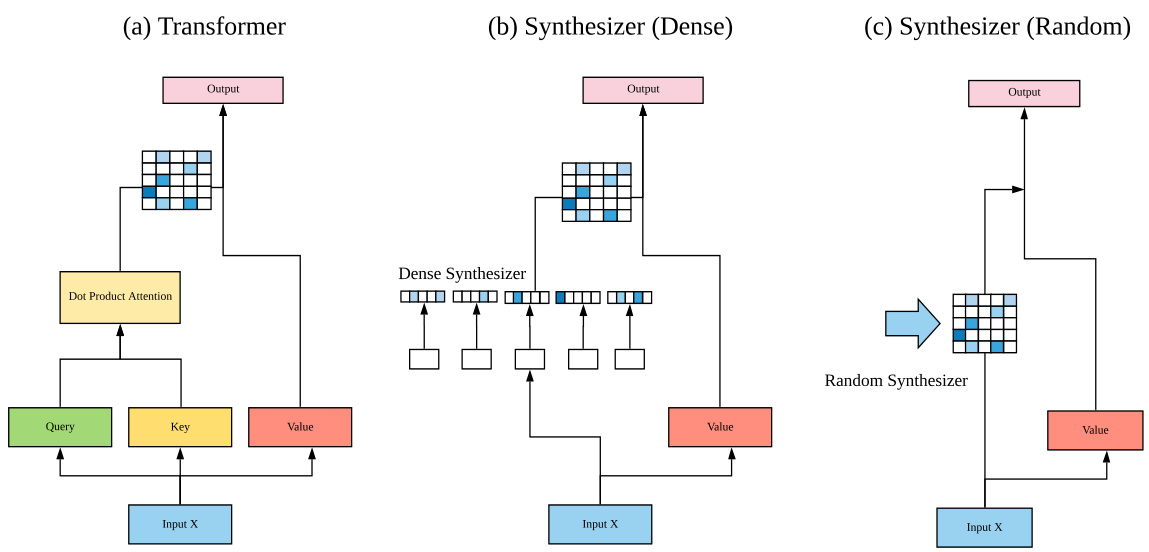
Figure 1. Our proposed SYNTHESIZER model architecture.
图 1: 我们提出的 SYNTHESIZER 模型架构。
$$
A_{h,\ell},B_{h,\ell}=F_{A,h,\ell}(X_{i,h,\ell}),F_{B,h,\ell}(X_{i,h,\ell})
$$
$$
A_{h,\ell},B_{h,\ell}=F_{A,h,\ell}(X_{i,h,\ell}),F_{B,h,\ell}(X_{i,h,\ell})
$$
where $F_{A,h,\ell}(.)$ projects input $X_{i,h,\ell}$ into $a$ dimensions, $F_{B,h,\ell}(.)$ projects $X_{i,h,\ell}$ to $b$ dimensions, and $a\times b=N$ . The output of the factorized module is now written as:
其中 $F_{A,h,\ell}(.)$ 将输入 $X_{i,h,\ell}$ 投影到 $a$ 维空间,$F_{B,h,\ell}(.)$ 将 $X_{i,h,\ell}$ 投影到 $b$ 维空间,且满足 $a\times b=N$。因子化模块的输出现可表示为:
$$
Y_{h,\ell}=\mathrm{softmax}(C_{h,\ell})G_{h,\ell}(X_{h,\ell}).
$$
$$
Y_{h,\ell}=\mathrm{softmax}(C_{h,\ell})G_{h,\ell}(X_{h,\ell}).
$$
where $C_{h,\ell}=H_{A}(A_{h,\ell})*H_{B}(B_{h,\ell})$ where $H_{A},H_{B}$ are tiling functions and $C_{h,\ell}\in\mathbb{R}^{N\times N}$ . The tiling function simply duplicates the vector $k$ times, i.e., $\mathbb{R}^{N}\rightarrow\overset{\cdot}{\mathbb{R}}^{N\times k}$ . In this case, $H_{A}(\cdot)$ is a projection of $\mathbb{R}^{a}\rightarrow\mathbb{R}^{a\times b}$ and $H_{B}(\cdot)$ is a projection of $\mathbb{R}^{b}\rightarrow\mathbb{R}^{b\times a}$ . To avoid having similar values within the same block, we compose the outputs of $H_{A}$ and $H_{B}$ .
其中 $C_{h,\ell}=H_{A}(A_{h,\ell})*H_{B}(B_{h,\ell})$ ,这里 $H_{A},H_{B}$ 是平铺函数,且 $C_{h,\ell}\in\mathbb{R}^{N\times N}$ 。平铺函数简单地将向量复制 $k$ 次,即 $\mathbb{R}^{N}\rightarrow\overset{\cdot}{\mathbb{R}}^{N\times k}$ 。在此情况下, $H_{A}(\cdot)$ 是 $\mathbb{R}^{a}\rightarrow\mathbb{R}^{a\times b}$ 的投影,而 $H_{B}(\cdot)$ 是 $\mathbb{R}^{b}\rightarrow\mathbb{R}^{b\times a}$ 的投影。为了避免同一块内出现相似值,我们对 $H_{A}$ 和 $H_{B}$ 的输出进行组合。
Factorized Random Synthesizer Similar to Factorized Synthesizers, we are also able to factorize $R_{h,\ell}$ into low rank matrices $R_{1,h,\ell},R_{2,h,\ell}\in\mathbb{R}^{N\times k}$ .
因子化随机合成器
与因子化合成器类似,我们也能将 $R_{h,\ell}$ 分解为低秩矩阵 $R_{1,h,\ell},R_{2,h,\ell}\in\mathbb{R}^{N\times k}$。
$$
Y_{h,\ell}=\mathrm{softmax}(R_{1,h,\ell}R_{2,h,\ell}^{\top})G_{h,\ell}(X_{h,\ell}).
$$
$$
Y_{h,\ell}=\mathrm{softmax}(R_{1,h,\ell}R_{2,h,\ell}^{\top})G_{h,\ell}(X_{h,\ell}).
$$
Therefore, it is easy to see that, for each head, this reduces the parameter costs from $N^{2}$ to $2(N k)$ where $k<<N$ and hence helps prevent over fitting. In practice, we use a small value of $k=8$ .
因此,可以明显看出,对于每个头(head),这将参数成本从$N^{2}$降低到$2(N k)$,其中$k<<N$,从而有助于防止过拟合。实际应用中,我们采用较小的$k=8$值。
Mixture of Synthesizers Finally, we note that all of the proposed synthetic attention variants can be mixed in an additive fashion. This can be expressed as:
合成器混合方案
最后需要指出的是,所有提出的合成注意力变体都可以通过加法方式进行混合。其数学表达为:
$$
\begin{array}{r l}&{Y_{h,\ell}=\mathrm{softmax}(\alpha_{1,h,\ell}S_{1,h,\ell}(X_{h,\ell})+}\ &{\cdot\cdot\cdot\alpha_{N,h,\ell}S_{N,h,e l l}(X_{h,\ell}))G_{h,\ell}(X_{h,\ell}).}\end{array}
$$
$$
\begin{array}{r l}&{Y_{h,\ell}=\mathrm{softmax}(\alpha_{1,h,\ell}S_{1,h,\ell}(X_{h,\ell})+}\ &{\cdot\cdot\cdot\alpha_{N,h,\ell}S_{N,h,e l l}(X_{h,\ell}))G_{h,\ell}(X_{h,\ell}).}\end{array}
$$
where $S(.)$ is a parameterized synthesizing function and the $\alpha$ (where $\textstyle\sum\alpha=1)$ are learnable weights. In the case of mixing R andom Factorized with standard Dense Synthesizers, this is expressed as:
其中 $S(.)$ 是一个参数化的合成函数,$\alpha$ (满足 $\textstyle\sum\alpha=1$) 是可学习的权重。在将随机因子化合成器与标准密集合成器混合的情况下,其表达式为:
$$
\begin{array}{r}{Y_{h,\ell}=\operatorname{softmax}(\alpha_{1,h,\ell}R_{1,h,\ell}R_{2,h,\ell}^{\top}+}\ {\alpha_{2,h,\ell}F_{h,\ell}(X_{h,\ell}))G_{h,\ell}(X).}\end{array}
$$
$$
\begin{array}{r}{Y_{h,\ell}=\operatorname{softmax}(\alpha_{1,h,\ell}R_{1,h,\ell}R_{2,h,\ell}^{\top}+}\ {\alpha_{2,h,\ell}F_{h,\ell}(X_{h,\ell}))G_{h,\ell}(X).}\end{array}
$$
We investigate several Mixture of Synthesizers variants in our experiments.
我们在实验中研究了多种混合合成器 (Mixture of Synthesizers) 变体。
On Parameters Depending on Sequence Length Random and dense Synthesizers both rely on parameters that depend on length $\ell$ . In general, we define a maximum length and dynamically truncate to the actual length of each batch. We note that this is in similar spirit to trainable positional encodings which have been common practice in Transformer models. Hence, we do not forsee any issue here. In the case that this is really a problem, one potential solution is to project to a smaller value $b$ and tile $b$ to the maximum sequence length. We leave this exploration to future work.
关于依赖序列长度的参数
随机和密集合成器都依赖于与长度$\ell$相关的参数。通常我们会设定一个最大长度,并根据每批次的实际长度进行动态截断。需要指出的是,这种做法与Transformer模型中常见的可训练位置编码思路相似。因此我们不认为这会带来问题。若确实存在隐患,一种可能的解决方案是将参数投影到较小值$b$,然后将$b$平铺至最大序列长度。我们将此探索留待后续研究。
3.2. Discussion
3.2. 讨论
This paper asks fundamental questions about the attention matrix $A$ and whether it is possible to synthesize $A$ by alternate means other than pairwise attention. It is worth noting that the regular dot product attention can also be subsumed by our SYNTHESIZER framework, i.e., SYNTHESIZER generalizes the Transformer model. In the case of the Transformer, the synthesizing function in question is $S(X)=F_{Q}(X)F_{K}(X)^{\top}$ . Table 1 lists the different model variants explored within our SYNTHESIZER framework. The ’condition on’ column refers to whether the synthesized output is produced as a function of $X_{i}$ or every $X_{i},X_{j}$ pair. The ‘sample‘ column indicates whether a given variant leverages local or global context. Random Synthesizers are global because they share the same global alignment patterns across all samples. Dense Synthesizers are considered to be local as they are conditioned on $X_{i}$ , which makes the alignment pattern dependent on each individual sample. To this end, it is imperative for synthesized models to have multiple heads to be effective.
本文对注意力矩阵$A$提出了根本性问题,探讨是否存在除成对注意力之外的其他方法能合成该矩阵。值得注意的是,常规点积注意力也可被纳入我们的SYNTHESIZER框架,即SYNTHESIZER推广了Transformer模型。在Transformer中,所涉及的合成函数为$S(X)=F_{Q}(X)F_{K}(X)^{\top}$。表1列出了我们在SYNTHESIZER框架中探索的不同模型变体。"condition on"列表示合成输出是作为$X_{i}$的函数还是每个$X_{i},X_{j}$对的函数。"sample"列表示给定变体是利用局部还是全局上下文。随机合成器(Random Synthesizers)属于全局型,因为它们在所有样本间共享相同的全局对齐模式。稠密合成器(Dense Synthesizers)被视为局部型,因其以$X_{i}$为条件,这使得对齐模式取决于每个独立样本。因此,合成模型必须具有多头机制才能有效运作。
表1:
Table 1. Overview of all Synthesizing Functions.
| Model | S(X) | ConditionOn | Sample | Interact | [0] |
| Dot Product | FQ(X)Fk(Xi)T | CA fX | Local | Yes | 2d2 |
| Random | R | N/A | Global | No | N2 |
| Fac.Random | R1R | N/A | Global | No | 2Nk |
| Dense | Fio(F2(Xi)) | Xi | Local | No | d² + dN |
| Fac. Dense | HA(FA(Xi))) *HB(FB(Xi))) | Xi | Local | No | d² + d(k1 + k2) |
表 1: 所有合成函数概述
| 模型 | S(X) | ConditionOn | Sample | Interact | [0] |
|---|---|---|---|---|---|
| 点积 (Dot Product) | FQ(X)Fk(Xi)T | CA fX | 局部 (Local) | 是 (Yes) | 2d2 |
| 随机 (Random) | R | N/A | 全局 (Global) | 否 (No) | N2 |
| 因子随机 (Fac.Random) | R1R | N/A | 全局 (Global) | 否 (No) | 2Nk |
| 密集 (Dense) | Fio(F2(Xi)) | Xi | 局部 (Local) | 否 (No) | d² + dN |
| 因子密集 (Fac. Dense) | HA(FA(Xi))) *HB(FB(Xi))) | Xi | 局部 (Local) | 否 (No) | d² + d(k1 + k2) |
4. Experiments
4. 实验
This section outlines our experimental setup and results. We first conduct experiments on five tasks to evaluate the effec ti ve ness 4 of different Synthesizer variants along with how they compare to the vanilla Transformer. Specifically, we conduct experiments on (1) machine translation (EnDe, EnFr) (2) auto regressive language modeling (LM1B) (3) text generation (sum mari z ation and dialogue modeling and (4) multi-task natural language processing (GLUE/SuperGLUE). Details of each experiments can be found in the appendix.
本节概述了我们的实验设置和结果。我们首先在五个任务上进行实验,以评估不同Synthesizer变体的有效性,并与原始Transformer进行比较。具体而言,我们在以下任务上进行了实验:(1) 机器翻译(EnDe, EnFr) (2) 自回归语言建模(LM1B) (3) 文本生成(摘要和对话建模) (4) 多任务自然语言处理(GLUE/SuperGLUE)。每个实验的详细信息可在附录中找到。
Notation of Variants We use R to denote Random, D to denote Dense and V to denote vanilla dot product attention. Fix to represent Fixed Random, FR to represent Factorized Random and FD to represent Factorized random. For Mixture Synthesizers, we use $^+$ to denote that two methods are mixed.
变体表示法
我们用 R 表示随机 (Random),D 表示稠密 (Dense),V 表示原始点积注意力 (vanilla dot product attention)。Fix 表示固定随机 (Fixed Random),FR 表示因子化随机 (Factorized Random),FD 表示因子化稠密 (Factorized Dense)。对于混合合成器 (Mixture Synthesizers),我们使用 $^+$ 表示两种方法的混合。
4.1. Comparing Synthesizer Variants and Transformer Models
4.1. 合成器变体与Transformer模型对比
This section dives into a detailed study of multiple Synthesizer variants and the base Transformer model.
本节深入研究多种Synthesizer变体及基础Transformer模型。
Experimental Results on MT/LM First, we observe that our Random Synthesizer baseline achieves 27.27 on EnDe and 41.12 on EnFr. The non-trainable (i.e., fixed) variant performs substantially worse, but still yields surprisingly strong $\approx24$ BLEU with fixed random attention weights. Most other SYNTHESIZER variants achieve competitive performance, although with slight performance degradation compared to Transformers. An interesting finding is that the Mixture model of Random $+$ Dense synthesizer performs comparably to vanilla Transformers on EnDe. When mixing the standard dot product attention, performance further increases by $+0.8$ BLEU points (EnDe). In general, the performance of SYNTHESIZER variants are competitive with Transformers for this task. On LM1b, We find that the Random Synthesizers perform within $1{-}2\mathrm{PPL}$ points away from the vanilla Transformer model. The best performing model is the Synthesizer $\mathrm{(D+V)}$ , which achieves the best performance on this setting.
MT/LM实验结果
首先,我们观察到随机合成器(Random Synthesizer)基线在英德(EnDe)任务上达到27.27分,在英法(EnFr)任务上达到41.12分。不可训练(即固定)变体表现明显较差,但使用固定随机注意力权重仍能获得约24 BLEU的惊人成绩。大多数其他合成器变体都取得了有竞争力的性能,尽管相比Transformer略有下降。一个有趣的发现是:随机+稠密合成器(Random+Dense synthesizer)的混合模型在英德任务上与原始Transformer表现相当。当混合标准点积注意力时,性能进一步提升+0.8 BLEU分(英德)。总体而言,合成器变体在此任务中的性能与Transformer不相上下。
在LM1b任务中,我们发现随机合成器的性能与原始Transformer模型相差1-2 PPL分。表现最佳的模型是合成器(D+V)变体,在该设定下取得了最优性能。
Results on Text Generation For sum mari z ation, we find that the (R) and (D) variants do not outperform Transformers. The performance of the (D) model is $\approx2$ Rouge-L points below Transformers. Hence, we postulate that the local sample-wise pairwise interactions are important for the sum mari z ation task. On the other hand, the utility of synthesized attention can also be observed, i.e., the $(\mathsf{R}+\mathsf{V})$ and $\left(\mathrm{R+D}\right)$ models both outperform Transformers. On the dialogue task, Synthesizers (R) and (D) both outperform vanilla Transformers by a reasonable margin $(\approx1-3)$ points across most/all metrics. The best performing model here is the (D) variant. Surprisingly, unlike most other tasks, the $(+\mathsf{V})$ variants do not perform well, signifying that dot product self-attention may actually be harmful for this task.
文本生成实验结果
在摘要任务中,我们发现(R)和(D)变体未能超越Transformer。(D)模型的Rouge-L分数比Transformer低约2分。因此,我们推测局部样本间成对交互对该任务至关重要。另一方面,合成注意力的优势依然可见:(R+V)和(R+D)模型均优于Transformer。在对话任务中,Synthesizer的(R)和(D)变体在所有/大部分指标上均以1-3分的优势超越原始Transformer,其中(D)变体表现最佳。值得注意的是,与其他任务不同,(V)变体在此表现不佳,这表明点积自注意力机制可能对该任务存在负面影响。
Table 3. Experimental results on Abstract ive Sum mari z ation (CNN/Dailymail) and Dialogue Generation (Person a Chat). We report on RL (Rouge-L), B4 (Bleu-4), Met. (Meteor) and CIDr.
| Model | Sum. RL B4 | RL | Dialogue Met. | CIDr |
| Trans. | 35.77 | 3.20 | 13.38 5.89 | 18.94 |
| SynthesizerModels | ||||
| R | 33.10 | 2.25 15.00 | 6.42 | 19.57 |
| D | 33.70 | 4.02 | 15.22 6.61 | 20.54 |
| D+V | 36.02 | 3.57 | 14.22 6.32 | 18.87 |
| R+V | 35.95 | 2.28 | 14.79 6.39 | 19.09 |
表 3: 摘要生成 (CNN/Dailymail) 和对话生成 (Persona Chat) 的实验结果。我们报告了 RL (Rouge-L)、B4 (Bleu-4)、Met. (Meteor) 和 CIDr 的指标。
| 模型 | Sum. RL B4 | RL | Dialogue Met. | CIDr |
|---|---|---|---|---|
| Trans. | 35.77 | 3.20 | 13.38 5.89 | 18.94 |
| SynthesizerModels | ||||
| R | 33.10 | 2.25 | 15.00 6.42 | 19.57 |
| D | 33.70 | 4.02 | 15.22 6.61 | 20.54 |
| D+V | 36.02 | 3.57 | 14.22 6.32 | 18.87 |
| R+V | 35.95 | 2.28 | 14.79 6.39 | 19.09 |
Comparing Synthesizers with Dynamic Convolutions To ascertain the competitiveness of Synthesizers, we also compare them with Dynamic convolutions (Wu et al., 2019).
比较合成器与动态卷积
为了验证合成器的竞争力,我们将其与动态卷积 (Dynamic convolutions) (Wu et al., 2019) 进行了对比。
| Model | NMT (BLEU) | LM (PPL) | |||
| [0] | EnDe | EnFr | [0] | LM | |
| Transformer' Transformer | 67M 67M | 27.30 27.67 | 38.10 41.57 | 70M | 38.21 |
| Synthesizer (Fixed Random) | 61M | 23.89 | 38.31 | 53M | 50.52 |
| Synthesizer (Random) | 67M | 27.27 | 41.12 | 58M | 40.60 |
| Synthesizer (Factorized Random) | 61M | 27.30 | 41.12 | 53M | 42.40 |
| Synthesizer (Dense) | 62M | 27.43 | 41.39 | 53M | 40.88 |
| Synthesizer(Factorized Dense) | 61M | 27.32 | 41.57 | 53M | 41.20 |
| Synthesizer (Random + Dense) | 67M | 27.68 | 41.21 | 58M | 42.35 |
| Synthesizer (Dense +Vanilla) | 74M | 27.57 | 41.38 | 70M | 37.27 |
| Synthesizer (Random + Vanilla) | 73M | 28.47 | 41.85 | 70M | 40.05 |
Table 2. Experimental Results on WMT’14 English-German, WMT’14 English-French Machine Translation tasks and Language Modeling One Billion (LM1B). $^\dagger$ denotes original r
