Parallel Scaling Law for Language Models

语言模型的并行扩展定律

Abstract

摘要

It is commonly believed that scaling language models should commit a significant space or time cost, by increasing the parameters (parameter scaling) or output tokens (inferencetime scaling). We introduce the third and more inference-efficient scaling paradigm: increasing the model’s parallel computation during both training and inference time. We apply $P$ diverse and learnable transformations to the input, execute forward passes of the model in parallel, and dynamically aggregate the $P$ outputs. This method, namely parallel scaling (PARSCALE), scales parallel computation by reusing existing parameters and can be applied to any model structure, optimization procedure, data, or task. We theoretically propose a new scaling law and validate it through large-scale pre-training, which shows that a model with $P$ parallel streams is similar to scaling the parameters by ${\mathcal{O}}(\log P)$ while showing superior inference efficiency. For example, PARSCALE can use up to $22\times$ less memory increase and $6\times$ less latency increase compared to parameter scaling that achieves the same performance improvement. It can also recycle an off-theshelf pre-trained model into a parallelly scaled one by post-training on a small amount of tokens, further reducing the training budget. The new scaling law we discovered potentially facilitates the deployment of more powerful models in low-resource scenarios, and provides an alternative perspective for the role of computation in machine learning.

人们普遍认为，扩展语言模型需要通过增加参数（参数扩展）或输出token（推理时间扩展）来付出显著的空间或时间成本。我们提出了第三种更具推理效率的扩展范式：在训练和推理期间同步增加模型的并行计算量。我们对输入施加$P$种多样化且可学习的变换，并行执行模型前向传播，并动态聚合$P$个输出。这种方法称为并行扩展（PARSCALE），通过复用现有参数实现并行计算扩展，可应用于任何模型结构、优化流程、数据或任务。我们理论上提出了新的扩展定律，并通过大规模预训练验证：具有$P$个并行流的模型相当于将参数扩展${\mathcal{O}}(\log P)$量级，同时展现出更优的推理效率。例如，在达到相同性能提升时，PARSCALE相比参数扩展可减少高达$22\times$的内存增长和$6\times$的延迟增长。该方法还能通过少量token的后训练，将现成预训练模型转化为并行扩展版本，进一步降低训练成本。我们发现的新扩展定律有望促进低资源场景下部署更强大的模型，并为计算在机器学习中的作用提供新视角。

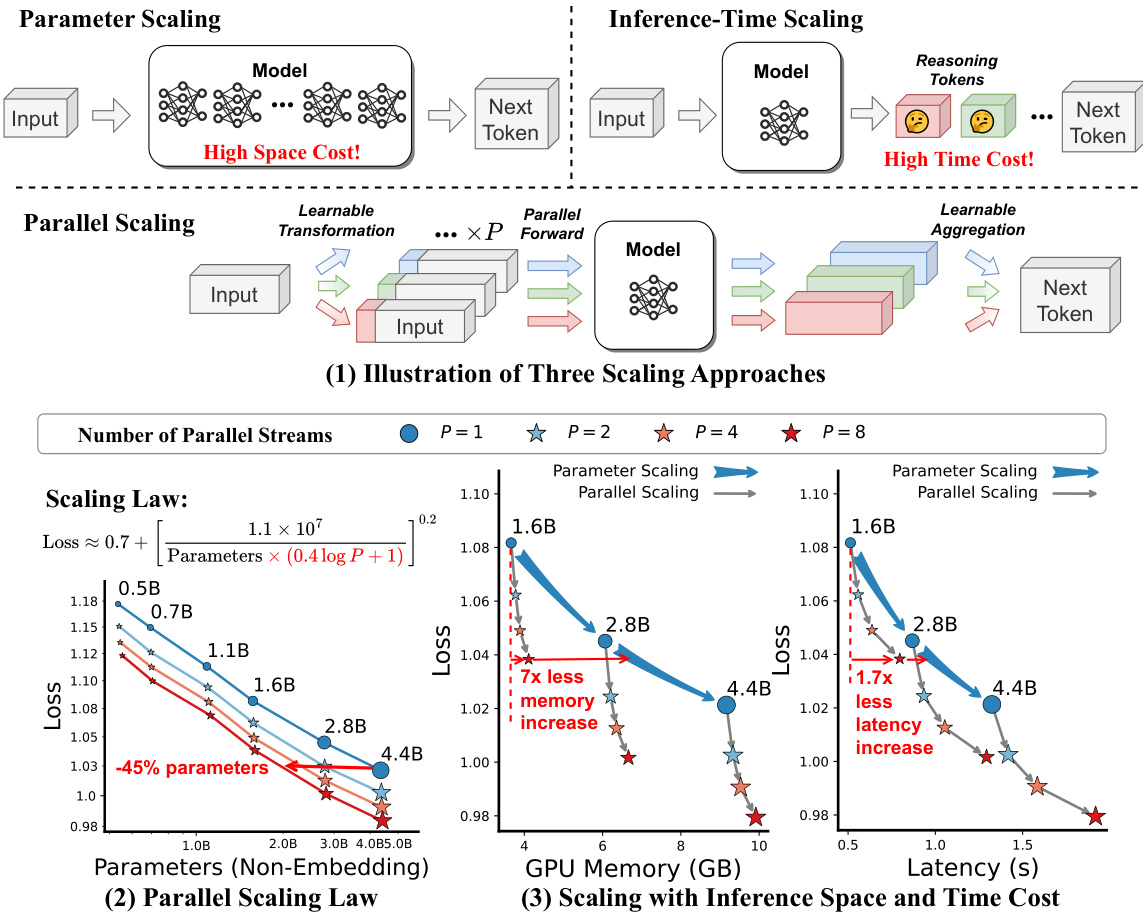
Figure 1: (1) Illustrations of our proposed parallel scaling (PARSCALE). (2) Parallel scaling laws for pre-training models on 42B tokens from Stack-V2 (Python subset). (3) Loss scaling curve with inference cost. Results are averaged from batch size $\in{1,2,4,\dot{8}}$ and input $^+$ output tokens $\check{\in}{128,256,512,1024}$ .

图 1: (1) 我们提出的并行扩展 (PARSCALE) 示意图。(2) 在 Stack-V2 (Python子集) 42B tokens 上预训练模型的并行扩展规律。(3) 推理成本随损失变化的缩放曲线。结果来自批量大小 $\in{1,2,4,\dot{8}}$ 和输入 $^+$ 输出 tokens $\check{\in}{128,256,512,1024}$ 的平均值。

1 Introduction

1 引言

Recent years have witnessed the rapid scaling of large language models (LLMs) (Brown et al., 2020; OpenAI, 2023; Llama Team, 2024; Qwen Team, 2025b) to narrow the gap towards Artificial General Intelligence (AGI). Mainstream efforts focus on parameter scaling (Kaplan et al., 2020), a practice that requires substantial space overhead. For example, DeepSeek-V3 (Liu et al., 2024a) scales the model size up to 672B parameters, which imposes prohibitive memory requirements for edge deployment. More recently, researchers have explored inference-time scaling (OpenAI, 2024) to enhance the reasoning capability by scaling the number of generated reasoning tokens. However, inference-time scaling is limited to certain scenarios and necessitates specialized training data (DeepSeek-AI, 2025; Qin et al., 2024), and typically imposes significant time costs. For example, Chen et al. (2024b) find that the most powerful models can generate up to 900 reasoning tokens for trivial problems like $^{\prime\prime}2+3{=}?^{\prime\prime}$ . This motivates the question: Is there a universal and efficient scaling approach that avoids excessive space and time costs?

近年来，大语言模型 (LLM) (Brown et al., 2020; OpenAI, 2023; Llama Team, 2024; Qwen Team, 2025b) 的快速扩展缩小了与通用人工智能 (AGI) 的差距。主流研究方向集中于参数扩展 (Kaplan et al., 2020) ，这种方法需要巨大的空间开销。例如，DeepSeek-V3 (Liu et al., 2024a) 将模型规模扩展至6720亿参数，这对边缘部署提出了极高的内存要求。最近，研究人员探索了推理时扩展 (OpenAI, 2024) ，通过增加生成推理 token 的数量来提升推理能力。然而，推理时扩展仅适用于特定场景，且需要专门的训练数据 (DeepSeek-AI, 2025; Qin et al., 2024) ，通常会带来显著的时间成本。例如，Chen et al. (2024b) 发现，最强大的模型针对简单问题 (如 $^{\prime\prime}2+3{=}?^{\prime\prime}$ ) 可生成多达900个推理 token 。这引发了一个问题：是否存在一种通用且高效的扩展方法，能够避免过高的空间和时间成本？

We draw inspiration from classifier-free guidance (CFG) (Ho & Salimans, 2022), a widely used trick during the inference phase of diffusion models (Ho et al., 2020), with similar concepts also developed in the NLP community (Sanchez et al., 2024; Li et al., 2023). Unlike traditional methods that use a single forward pass, CFG utilizes two forward passes during inference: it first performs a normal forward pass to obtain the first stream of output, then perturbs the input (e.g., by discarding conditions in the input) to get a second stream of output. The two streams are aggregated based on predetermined contrastive rules, yielding superior performance over single-pass outputs. Despite its widespread use, the theoretical guarantee of CFG remains an open question. In this paper, we hypothesize that the effectiveness of CFG lies in its double computation. We further propose the following hypothesis:

我们从无分类器引导 (CFG) (Ho & Salimans, 2022) 中获得灵感，这是扩散模型 (Ho et al., 2020) 推理阶段广泛使用的技巧，类似概念也在 NLP 领域得到发展 (Sanchez et al., 2024; Li et al., 2023)。与传统单次前向传播方法不同，CFG 在推理时采用两次前向传播：先执行正常前向传播获得第一路输出，再扰动输入（例如丢弃输入条件）获得第二路输出。两路输出根据预设的对比规则进行聚合，其性能优于单次传播输出。尽管 CFG 被广泛使用，但其理论保证仍是一个开放性问题。本文假设 CFG 的有效性源于其双重计算机制，并进一步提出以下假设：

Hypothesis 1. Scaling parallel computation (while maintaining the nearly constant parameters) enhances the model’s capability, with similar effects as scaling parameters.

假设1. 扩展并行计算规模 (同时保持参数几乎恒定) 能提升模型能力，其效果与扩展参数规模类似。

We propose a proof-of-concept scaling approach called parallel scaling (PARSCALE) to validate this hypothesis on language models. The core idea is to increase the number of parallel streams while making the input transformation and output aggregation learnable. We propose appending $P$ different learnable prefixes to the input and feeding them in parallel into the model. These $\bar{P}$ outputs are then aggregated into a single output using a dynamic weighted sum, as shown in Figure 1(1). This method efficiently scales parallel computation during both training and inference time by recycling existing parameters, which applies to various training algorithms, data, and tasks.

我们提出了一种名为并行扩展 (PARSCALE) 的概念验证扩展方法，用于验证大语言模型上的这一假设。其核心思想是在保持输入转换和输出聚合可学习的同时增加并行流数量。具体实现是为输入附加 $P$ 个不同的可学习前缀 (learnable prefix) ，并并行输入模型，随后通过动态加权求和将这 $\bar{P}$ 个输出聚合成单一输出，如图 1(1) 所示。该方法通过复用现有参数，在训练和推理阶段高效扩展并行计算能力，适用于各类训练算法、数据及任务。

Our preliminary theoretical analysis suggests that the loss of PARSCALE may follow a power law similar to the Chinchilla scaling law (Hoffmann et al., 2022). We then carry out large-scale pre-training experiments on the Stack-V2 (Lozhkov et al., 2024) and Pile (Gao et al., 2021) corpus, by ranging $P$ from 1 to 8 and model parameters from 500M to 4.4B. We use the results to fit a new parallel scaling law that generalizes the Chinchilla scaling law, as depicted in Figure 1(2). It shows that parallel i zing into $\mathbf{P}$ streams equates to scaling the model parameters by ${\mathcal{O}}(1{\bf o g}P)$ . Results on comprehensive tasks corroborate this conclusion. Unlike parameter scaling, PARSCALE introduces negligible parameters and increases only a little space overhead. It also leverages GPU-friendly parallel computation, shifting the memory bottleneck in LLM decoding to a computational bottleneck and, therefore, does not notably increase latency. For example, for a 1.6B model, when scaling to $P=8$ using PARSCALE, it uses $\bf{22\times}$ less memory increase and $6\times$ less latency increase compared to parameter scaling that achieves the same model capacity (batch size $=1$ , detailed in Section 3.3). Figure 1(3) illustrates that PARSCALE offers superior inference efficiency.

我们的初步理论分析表明，PARSCALE的损失可能遵循类似于Chinchilla缩放律 (Hoffmann et al., 2022) 的幂律。随后我们在Stack-V2 (Lozhkov et al., 2024) 和Pile (Gao et al., 2021) 语料库上进行了大规模预训练实验，将$P$从1调整到8，模型参数从500M调整到4.4B。我们利用这些结果拟合了一个新的并行缩放律，该定律推广了Chinchilla缩放律，如图1(2)所示。结果表明，将模型并行化为$\mathbf{P}$个流相当于将模型参数缩放${\mathcal{O}}(1{\bf o g}P)$。在综合任务上的结果验证了这一结论。与参数缩放不同，PARSCALE引入的参数可忽略不计，仅略微增加空间开销。它还利用了对GPU友好的并行计算，将大语言模型解码中的内存瓶颈转移为计算瓶颈，因此不会显著增加延迟。例如，对于一个1.6B的模型，当使用PARSCALE缩放到$P=8$时，与达到相同模型容量的参数缩放相比 (批大小$=1$，详见第3.3节)，其内存增加量减少了$\bf{22\times}$，延迟增加量减少了$6\times$。图1(3)展示了PARSCALE具有更优的推理效率。

Furthermore, we show that the high training cost of PARSCALE can be reduced by a two-stage approach: the first stage employs traditional training with most of the training data, and PARSCALE is applied only in the second stage with a small number of tokens. Based on this, we train 1.8B models with various $\dot{P}$ and scale the training data to 1T tokens. The results of 21 downstream benchmarks indicate the efficacy of this strategy. For example, when scaling to $P=8$ , it yields a $34%$ relative improvement for GSM8K and $23%$ relative improvement for MMLU using exactly the same training data. We also implement PARSCALE on an off-the-shelf model, Qwen-2.5 (Qwen Team, 2024), and demonstrate that PARSCALE is effective in both full and parameter-efficient fine-tuning settings. This also shows the viability of dynamic parallel scaling, which allows flexible adjustment of $\breve{P}$ during deployment while freezing the backbone weights, to fit different application scenerios.

此外，我们还展示了降低PARSCALE高训练成本的二阶段方案：第一阶段使用传统方法训练大部分数据，仅在第二阶段对少量token应用PARSCALE。基于此，我们训练了1.8B参数的多种 $\dot{P}$ 模型，并将训练数据规模扩展至1T token。21个下游基准测试结果表明该策略的有效性。例如当扩展到 $P=8$ 时，在完全相同的训练数据下，GSM8K相对提升34%，MMLU相对提升23%。我们还在现成模型Qwen-2.5 (Qwen Team, 2024)上实现了PARSCALE，证明其在全参数微调和参数高效微调场景均有效。这也展示了动态并行扩展的可行性——部署时在冻结主干权重的前提下灵活调整 $\breve{P}$ ，以适应不同应用场景。

Table 1 compares PARSCALE with other mainstream scaling strategies. Beyond introducing an efficient scaling approach for language models, our research also tries to address a more fundamental question in machine learning: Is a model’s capacity determined by the parameters or by the computation, and what is their individual contribution? Traditional machine learning models typically scale both parameters and computation simultaneously, making it difficult to determine their contribution ratio. The PARSCALE and the fitted parallel scaling law may offer a novel and quantitative perspective on this problem.

表 1 比较了 PARSCALE 与其他主流缩放策略。除了为语言模型引入一种高效的缩放方法外，我们的研究还试图解决机器学习中一个更基础的问题：模型的能力是由参数还是计算决定的，它们各自的贡献是什么？传统机器学习模型通常会同时缩放参数和计算，因此难以确定它们的贡献比例。PARSCALE 和拟合的并行缩放定律可能为这个问题提供一个新颖的定量视角。

Table 1: Comparisons of mainstream LLM scaling strategies. We subdivide parameter scaling into traditional Dense Scaling and Mixture-of-Expert (MoE) Scaling (Fedus et al., 2022) for comparison. Inference-Time Scaling: Enhancing the reasoning ability through large-scale reinforcement learning (RL) to scale reasoning tokens during inference.

表 1: 主流大语言模型扩展策略对比。我们将参数扩展细分为传统密集扩展 (Dense Scaling) 和混合专家扩展 (Mixture-of-Expert Scaling, MoE) (Fedus et al., 2022) 进行对比。推理时扩展 (Inference-Time Scaling): 通过大规模强化学习 (RL) 提升推理能力，在推理过程中扩展推理 token。

方法	推理时间	推理空间	训练成本	专用策略
密集扩展	中等	高	仅需预训练	无
混合专家扩展	极低	高	仅需预训练	负载均衡
推理时扩展	高	中等	需后训练	强化学习/奖励数据
并行扩展	中等	中等	需预训练或后训练	无

We posit that large computing can foster the emergence of large intelligence. We hope our work can inspire more ways to scaling computing towards AGI and provide insights for other areas of machine learning. Our key findings in this paper can be summarized as follows:

我们认为大规模计算能够促进大规模智能的出现。希望我们的工作能激发更多通过扩展计算实现通用人工智能 (AGI) 的方法，并为机器学习其他领域提供启示。本文的核心发现可归纳如下:

Our code and 67 trained model checkpoints are publicly available at https://github.com/QwenLM/ ParScale and https://hugging face.co/ParScale.

我们的代码和67个训练好的模型检查点已在 https://github.com/QwenLM/ParScale 和 https://huggingface.co/ParScale 公开提供。

2 Background and Methodology

2 背景与方法论

Classifier-Free Guidance (CFG) CFG (Ho & Salimans, 2022) has become a de facto inference-time trick in diffusion models (Ho et al., 2020), with similar concepts also developed in NLP (Sanchez et al., 2024; Li et al., 2023). At a high level, these lines of work can be summarized as follows: given an input $x\in\mathbb{R}^{d_{i}}$ and a trained model $f_{\theta}:\mathbb{R}^{d_{i}}\rightarrow\mathbb{R}^{d_{o}}$ , where $\theta$ is the parameter and $d_{i},d_{o}$ are dimensions, we transform $x$ into a $\mathrm{^{//}b a d^{\prime\prime}}$ version $x^{\prime}$ based on some heuristic rules (e.g., removing conditions), obtaining two parallel outputs $f_{\boldsymbol{\theta}}(\boldsymbol{x})$ and $f_{\boldsymbol\theta}(x^{\prime})$ . The final output $g_{\boldsymbol{\theta}}(\boldsymbol{x})$ is aggregated based on the following rule:

无分类器引导 (CFG)
CFG (Ho & Salimans, 2022) 已成为扩散模型 (Ho et al., 2020) 中实际采用的推理技巧，类似概念也在自然语言处理领域得到发展 (Sanchez et al., 2024; Li et al., 2023)。高层次来看，这些工作可概括为：给定输入 $x\in\mathbb{R}^{d_{i}}$ 和训练好的模型 $f_{\theta}:\mathbb{R}^{d_{i}}\rightarrow\mathbb{R}^{d_{o}}$ ，其中 $\theta$ 是参数，$d_{i},d_{o}$ 是维度，我们基于某些启发式规则 (例如移除条件) 将 $x$ 转换为 $\mathrm{^{//}b a d^{\prime\prime}}$ 版本 $x^{\prime}$ ，获得两个并行输出 $f_{\boldsymbol{\theta}}(\boldsymbol{x})$ 和 $f_{\boldsymbol\theta}(x^{\prime})$ 。最终输出 $g_{\boldsymbol{\theta}}(\boldsymbol{x})$ 按以下规则聚合：

$$
g_{\theta}(x)=f_{\theta}(x)+w\left(f_{\theta}(x)-f_{\theta}(x^{\prime})\right).
$$

$$
g_{\theta}(x)=f_{\theta}(x)+w\left(f_{\theta}(x)-f_{\theta}(x^{\prime})\right).
$$

Here, $w>0$ is a pre-set hyper parameter. Intuitively, Equation (1) can be seen as starting from a “good” prediction and moving $w$ steps in the direction away from a “bad” prediction. Existing research shows that $g_{\boldsymbol{\theta}}(\boldsymbol{x})$ can perform better than the vanilla $f_{\boldsymbol{\theta}}(\boldsymbol{x})$ in practice (Saharia et al., 2022).

这里，$w>0$ 是一个预设的超参数。直观上，式 (1) 可以看作是从一个"好"的预测开始，然后朝着远离"坏"预测的方向移动 $w$ 步。现有研究表明，$g_{\boldsymbol{\theta}}(\boldsymbol{x})$ 在实践中表现优于原始模型 $f_{\boldsymbol{\theta}}(\boldsymbol{x})$ (Saharia et al., 2022)。

Motivation In Equation (1), $x^{\prime}$ is simply a degraded version of $x,$ suggesting that $g_{\boldsymbol{\theta}}(\boldsymbol{x})$ does not gain more useful information than $f_{\boldsymbol{\theta}}(x)$ . This raises the question: why is $f_{\boldsymbol{\theta}}(x)$ unable to learn the capability of $g_{\boldsymbol{\theta}}(\boldsymbol{x})$ during training, despite both having the same parameters? We hypothesize that the fundamental reason lies in $g_{\boldsymbol{\theta}}(\boldsymbol{x})$ having twice the computation as $f_{\boldsymbol{\theta}}(\boldsymbol{\bar{x}})$ . This inspires us to further expand Equation (1) into the following form:

动机 在公式 (1) 中，$x^{\prime}$ 仅是 $x$ 的退化版本，这表明 $g_{\boldsymbol{\theta}}(\boldsymbol{x})$ 并未获得比 $f_{\boldsymbol{\theta}}(x)$ 更有用的信息。这引发了一个问题：为什么 $f_{\boldsymbol{\theta}}(x)$ 在训练期间无法学习 $g_{\boldsymbol{\theta}}(\boldsymbol{x})$ 的能力，尽管两者具有相同的参数？我们假设根本原因在于 $g_{\boldsymbol{\theta}}(\boldsymbol{x})$ 的计算量是 $f_{\boldsymbol{\theta}}(\boldsymbol{\bar{x}})$ 的两倍。这启发我们将公式 (1) 进一步扩展为以下形式：

$$
g_{\theta}(x)=w_{1}f_{\theta}(x_{1})+w_{2}f_{\theta}(x_{2})+\cdot\cdot\cdot+w_{P}f_{\theta}(x_{P}),
$$

$$
g_{\theta}(x)=w_{1}f_{\theta}(x_{1})+w_{2}f_{\theta}(x_{2})+\cdot\cdot\cdot+w_{P}f_{\theta}(x_{P}),
$$

where $P$ denotes the number of parallel streams. $x_{1},\cdots,x_{P}$ are $P$ distinct transformations of $x,$ and $w_{1},\cdots,w_{P}$ are aggregation weights. We term Equation (2) as a parallel scaling (PARSCALE) of the model $f_{\theta}$ with $P$ streams. This scaling strategy does not require changing the structure of $f_{\theta}$ and training data. In this paper, we focus on Transformer language models (Vaswani et al., 2017; Brown et al., 2020), and regard the stacked Transformer layers as $f_{\theta}\breve{(\cdot)}$ .

其中 $P$ 表示并行流的数量。$x_{1},\cdots,x_{P}$ 是 $x$ 的 $P$ 种不同变换，$w_{1},\cdots,w_{P}$ 是聚合权重。我们将公式 (2) 称为模型 $f_{\theta}$ 的 $P$ 流并行扩展 (PARSCALE)。这种扩展策略无需改变 $f_{\theta}$ 的结构和训练数据。本文聚焦于 Transformer 语言模型 (Vaswani et al., 2017; Brown et al., 2020)，并将堆叠的 Transformer 层视为 $f_{\theta}\breve{(\cdot)}$。

Implementation Details and Pivot Experiments We apply Equation (2) in both training and inference time, and perform a series of pivot experiments to determine the best input transformation and output aggregation strategies (refer to Appendix A). The findings revealed that variations in these strategies minimally affect model performance; the significant factor is the number of computations (i.e., P). Finally, for input transformation, we employ prefix tuning (Li & Liang, 2021) as the input transformation, which is equivalent to using different KV-caches to distinguish different streams. For output aggregation, we employ a dynamic weighted average approach, utilizing an MLP to convert outputs from multiple streams into aggregation weights. This increases about $0.2%$ additional parameters for each stream.

实现细节与关键实验
我们在训练和推理阶段均应用公式(2)，并通过一系列关键实验确定最佳输入转换与输出聚合策略（详见附录A）。研究发现这些策略的差异对模型性能影响甚微，关键影响因素是计算量（即P值）。最终，在输入转换方面采用前缀调优(Li & Liang, 2021)技术，其效果等同于使用不同的KV缓存区分不同数据流；输出聚合则采用动态加权平均法，通过MLP将多流输出转换为聚合权重。该方法为每个流增加约$0.2%$的额外参数量。

3 Parallel Scaling Law

3 并行扩展定律

This section focuses on the in-depth comparison of scaling parallel computation with scaling parameters. In Section 3.1, we theoretically demonstrate that parallel scaling is equivalent to increasing parameters by a certain amount. In Section 3.2, we validate this with a practical scaling law through large-scale experiments. Finally, in Section 3.3, we analyze latency and memory usage during inference to show that parallel scaling is more efficient.

本节重点深入比较并行计算扩展与参数扩展的效果。在3.1节中，我们从理论上证明并行扩展等效于增加一定数量的参数。在3.2节中，我们通过大规模实验用实际扩展定律验证了这一结论。最后在3.3节中，我们分析了推理过程中的延迟和内存使用情况，表明并行扩展效率更高。

3.1 Theoretical Analysis: Can PARSCALE Achieve Similar Effects as Parameter Scaling?

3.1 理论分析：PARSCALE能否实现与参数缩放(Parameter Scaling)类似的效果？

From another perspective, PARSCALE can be seen as an ensemble of multiple different next token predictions, despite the ensemble components sharing most of the parameters. Existing theory in literature finds that the ensembling performance depends on the diversity of different components (Breiman, 2001; Lobacheva et al., 2020b). In this section, we further validate this finding by theoretically proposing a new scaling law that generalizes existing language model scaling laws, and demonstrate that PARSCALE can achieve similar effects as parameter scaling.

从另一个角度来看，PARSCALE 可视为多个不同下一 Token 预测的集成，尽管这些集成组件共享大部分参数。现有文献理论发现，集成性能取决于不同组件的多样性 (Breiman, 2001; Lobacheva et al., 2020b)。本节中，我们通过理论提出一种能泛化现有大语言模型缩放律的新缩放律，进一步验证这一发现，并证明 PARSCALE 能实现与参数缩放类似的效果。

We consider a special case that $w_{1}=w_{2}=\cdot\cdot\cdot=1/P$ to simplify our analysis. This is a degraded version of PARSCALE, therefore, we can expect that the full version of PARSCALE is at least not worse than the theoretical results we can obtain (See Appendix A for further numeric comparison). Let ${\hat{p}}_{i}(\cdot\mid x)=f_{\theta}(x_{i})$ denote the next token distribution for the input sequence $x$ predicted by the $i$ -th stream. Based on Equation (2), the final prediction ${\hat{p}}(\cdot\mid x)=g_{\theta}{\dot{(x)}}$ is the average across ${\hat{p}}_{i},$ i.e., $\hat{p}(\cdot\mid x)=1/{\cal P}\sum_{i}\hat{p}_{i}(\cdot\mid x)$ . Chinchilla (Hoffmann et al., 2022) proposes that the loss $\mathcal{L}$ of a language model with $N$ parameters is a function of $N$ after convergence. We assume the prediction of each stream adheres to the Chinchilla scaling law, as follows:

我们考虑一个特殊情况 $w_{1}=w_{2}=\cdot\cdot\cdot=1/P$ 以简化分析。这是 PARSCALE 的简化版本，因此可以预期完整版 PARSCALE 至少不会逊色于我们获得的理论结果（具体数值比较参见附录 A）。设 ${\hat{p}}_{i}(\cdot\mid x)=f_{\theta}(x_{i})$ 表示第 $i$ 个流对输入序列 $x$ 预测的下一 token 分布。根据公式 (2)，最终预测 ${\hat{p}}(\cdot\mid x)=g_{\theta}{\dot{(x)}}$ 是各 ${\hat{p}}_{i}$ 的平均值，即 $\hat{p}(\cdot\mid x)=1/{\cal P}\sum_{i}\hat{p}_{i}(\cdot\mid x)$。Chinchilla (Hoffmann et al., 2022) 提出，大语言模型收敛后的损失 $\mathcal{L}$ 是其参数量 $N$ 的函数。我们假设每个流的预测都遵循 Chinchilla 缩放律，如下所示：

Lemma 3.1 (Chinchilla Scaling Law (Hoffmann et al., 2022)). The language model cross-entropy loss $\mathcal{L}_{i}$ for the i-th stream prediction (with $N$ parameters) when convergence is:

引理 3.1 (Chinchilla 缩放定律 (Hoffmann et al., 2022))。当收敛时，第i个流预测（具有$N$个参数）的语言模型交叉熵损失$\mathcal{L}_{i}$为：

$$
\mathcal{L}_{i}=\left(\frac{A}{N}\right)^{\alpha}+E,\quad1\leq i\leq P,
$$

$$
\mathcal{L}_{i}=\left(\frac{A}{N}\right)^{\alpha}+E,\quad1\leq i\leq P,
$$

where ${A,E,\alpha}$ are some positive constants. $E$ is the entropy of natural text, and $N$ is the number of parameters.1

其中 ${A,E,\alpha}$ 为正常数。$E$ 表示自然文本的熵，$N$ 为参数量。1

Based on Lemma 3.1, we theoretically derive that after aggregating $P$ streams, the prediction follows a new type of scaling law, as follows:

根据引理3.1，我们从理论上推导出聚合$P$个流后，预测遵循一种新型的缩放定律，如下所示：

Proposition 1 (Theoretical Formula for Parallel Scaling Law). The loss $\mathcal{L}$ for PARSCALE (with $P$ streams and $N$ parameters) is

命题 1 (并行扩展律的理论公式). PARSCALE (含 $P$ 个数据流和 $N$ 个参数) 的损失 $\mathcal{L}$ 满足

$$
{\mathcal{L}}=\left({\frac{A}{N\cdot P^{1/\alpha}\cdot{\mathrm{DIVERSITY}}}}\right)^{\alpha}+E.
$$

$$
{\mathcal{L}}=\left({\frac{A}{N\cdot P^{1/\alpha}\cdot{\mathrm{DIVERSITY}}}}\right)^{\alpha}+E.
$$

We define DIVERSITY as:

我们将DIVERSITY定义为：

$$
\begin{array}{r}{\mathrm{DIVERSITY}=\left[(P-1)\rho+1\right]^{-1/\alpha},}\end{array}
$$

$$
\begin{array}{r}{\mathrm{DIVERSITY}=\left[(P-1)\rho+1\right]^{-1/\alpha},}\end{array}
$$

where $\rho$ is the correlation coefficient between random variables $\Delta{{p}{i}}$ and $\Delta p_{j}(i\neq j),$ and $\Delta{{p}{i}}$ is the relative residuals for the i-th stream prediction, i.e., $\Delta p_{i}=\lceil\hat{p}_{i}(y|x)-p(y|x)\rceil/p(y|x)$ . $p(y\mid x)$ is the real next token probability.

其中 $\rho$ 是随机变量 $\Delta{{p}{i}}$ 和 $\Delta p_{j}(i\neq j)$ 之间的相关系数，$\Delta{{p}{i}}$ 是第i个流预测的相对残差，即 $\Delta p_{i}=\lceil\hat{p}_{i}(y|x)-p(y|x)\rceil/p(y|x)$。$p(y\mid x)$ 是真实的下一个token概率。

Proof for Proposition 1 is elaborated in Appendix B. From it, we can observe two key insights:

命题1的证明详见附录B。由此我们可以得出两个关键结论:

1. When $\rho=1$ , predictions across different streams are identical, at which point we can validate that Equation (4) degenerates into Equation (3). Random initialization on a small number of parameters introduced (i.e., prefix embeddings) is sufficient to avoid this situation in our experiments, likely due to the impact being magnified by the extensive computation of LLMs.
2. 当 $\rho=1$ 时，不同流之间的预测结果相同，此时可以验证方程 (4) 退化为方程 (3)。在我们的实验中，仅需对少量引入的参数（即前缀嵌入）进行随机初始化即可避免这种情况，这可能是由于大语言模型 (LLM) 的庞大计算量放大了影响效果。
3. When $\rho\neq1$ , $\mathcal{L}$ is inversely correlated to $P$ . Notably, when $\rho=0.$ , residuals are independent between streams and the training loss exhibits a power-law relationship with $P$ (i.e., $\mathcal{L}\propto P^{-1}$ ). This aligns with findings in Lobacheva et al. (2020b). When $\rho$ is negative, the loss can further decrease and approach zero. This somewhat de mystifies the effectiveness of CFG: by widening the gap between $'^{\prime\prime}\mathrm{good}^{\prime\prime}$ input $x$ and “bad” input $x^{\prime}$ , we force the model to “think” from two distinct perspectives, which can increase the diversity between the two outputs.
4. 当 $\rho\neq1$ 时，$\mathcal{L}$ 与 $P$ 呈负相关。值得注意的是，当 $\rho=0.$ 时，流之间的残差相互独立，训练损失与 $P$ 呈现幂律关系 (即 $\mathcal{L}\propto P^{-1}$)。这一发现与 Lobacheva 等人 (2020b) 的研究结果一致。当 $\rho$ 为负值时，损失可以进一步降低并趋近于零。这在一定程度上解释了分类器无关引导 (CFG) 的有效性：通过扩大“好”输入 $x$ 与“坏”输入 $x^{\prime}$ 之间的差距，我们迫使模型从两个不同角度进行“思考”，从而增加两个输出之间的多样性。

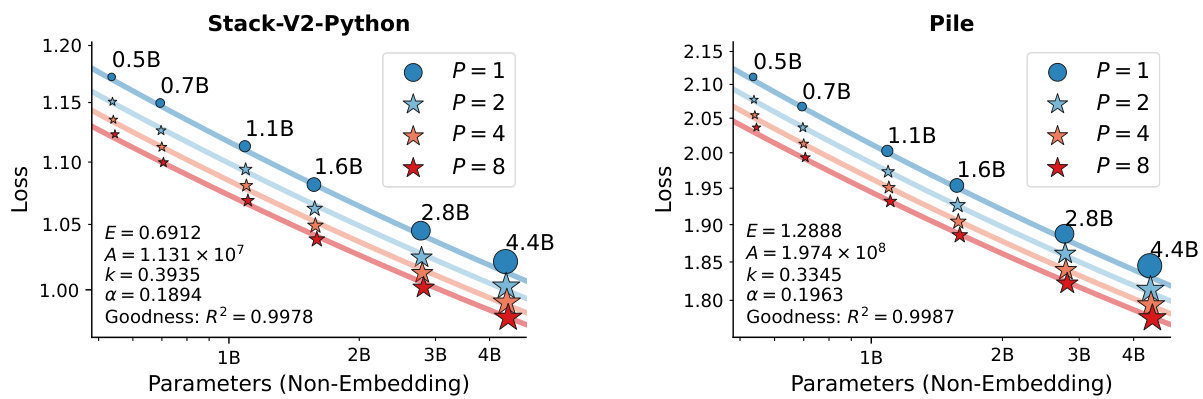
Figure 2: Loss of LLMs scaled on parameters and number of parallel streams $P$ trained on 42B tokens. Each point depicts the loss from a training run. The fitted scaling law curve from Equation (5) is displayed, with annotated fitted parameters $\left(E,A,k,\alpha\right)$ and the goodness of fit $R^{2}$ .

图 2: 大语言模型 (LLM) 在参数量和并行流数量 $P$ 下的损失变化 (基于 42B token 训练) 。每个点代表一次训练运行的损失值。图中展示了根据公式 (5) 拟合的缩放律曲线，并标注了拟合参数 $\left(E,A,k,\alpha\right)$ 以及拟合优度 $R^{2}$ 。

Despite the difficulty in further modeling $\rho_{,}$ Proposition 1 suggests that scaling $P$ times of parallel computation is equivalent to scaling the model parameter count, by a factor of ( $P^{\Psi\alpha}$ ·DIVERSITY). This motivates us to go further, by empirically fitting a practical parallel scaling law to validate Hypothesis 1.

尽管难以进一步建模 $\rho_{,}$，但命题 1 表明，将并行计算规模扩展 $P$ 倍，等效于将模型参数量按 ( $P^{\Psi\alpha}$ ·DIVERSITY) 的系数进行扩展。这激励我们通过实证拟合实用的并行扩展定律来进一步验证假设 1。

3.2 Practical Parallel Scaling Laws

3.2 实际并行扩展定律

Experiment Setup To fit a parallel scaling law in practice, we pre-train Transformer language models with the Qwen-2.5 dense architecture and tokenizer (Qwen Team, 2024) from scratch on the open-source corpus. Models have up to 4.7 billion parameters (with 4.4B non-embedding parameters) and 8 parallel streams. We primarily focus on the relationship between parallel scaling and parameter scaling. Therefore, we fix the training data size at 42 billion tokens without data repeat2. We introduce the results for more training tokens in the next section, and leave the impact of data scale on our scaling laws for future work. We use a batch size of 1024 and a sequence length of 2048, resulting in 20K training steps. For models with $P>1$ , we incorporate prefix embeddings and aggregation weight, as introduced in Appendix A. No additional parameters are included for $P=\stackrel{\smile}{1}$ models to maintain alignment with existing architectures. We report the last step training loss using exponential moving average, with a smoothing weight of 0.95. Other hyper parameters follow existing works (Mu en nigh off et al., 2023) and are detailed in Appendix C.

实验设置
为在实践中拟合并行扩展规律，我们使用Qwen-2.5密集架构和分词器（Qwen Team, 2024）从头开始在开源语料库上预训练Transformer语言模型。模型参数规模最高达47亿（含44亿非嵌入参数），支持8个并行流。我们主要关注并行扩展与参数扩展之间的关系，因此将训练数据量固定为420亿token且不重复使用数据。更多训练token的结果将在下一节展示，数据规模对扩展规律的影响留待未来研究。我们采用1024的批次大小和2048的序列长度，共进行2万次训练步。对于$P>1$的模型，如附录A所述，我们加入了前缀嵌入和聚合权重。$P=\stackrel{\smile}{1}$模型则未引入额外参数以保持与现有架构的一致性。训练损失采用平滑权重为0.95的指数移动平均法记录最终步结果。其余超参数遵循现有研究（Muennighoff et al., 2023），详见附录C。

Our pre-training is conducted on two widely utilized datasets: Stack-V2 (Python subset) (Lozhkov et al., 2024) and Pile (Gao et al., 2021). Pile serves as a general corpus aimed at enhancing common sense and memorization skills, while Stack-V2 focuses on code comprehension and reasoning skills. Analyzing PARSCALE across these contexts can assess how parameters and computations contribute to different skills.

我们的预训练基于两个广泛使用的数据集：Stack-V2 (Python子集) (Lozhkov等人，2024) 和 Pile (Gao等人，2021)。Pile作为通用语料库旨在提升常识记忆能力，而Stack-V2专注于代码理解与推理能力。通过在这些场景下分析PARSCALE，可以评估参数与计算对不同技能的影响。

Parametric Fitting We plot the results in Figure 2, where each point represents the loss of a training run, detailed in Appendix F. We observe that increasing $P$ yields benefits following a logarithmic trend. Similar gains are seen when raising $P$ from 1 to 2, 2 to 4, and 4 to 8. Thus, we preliminarily try the following form:

参数化拟合
我们将结果绘制在图 2 中，其中每个点代表一次训练运行的损失（详见附录 F）。我们观察到，增加 $P$ 会带来对数趋势的收益。当 $P$ 从 1 提升到 2、2 到 4 以及 4 到 8 时，也观察到了类似的增益。因此，我们初步尝试以下形式：

$$
{\mathcal{L}}=\left({\frac{A}{N\cdot(k\log P+1)}}\right)^{\alpha}+E,
$$

$$
{\mathcal{L}}=\left({\frac{A}{N\cdot(k\log P+1)}}\right)^{\alpha}+E,
$$

where we assume that $P^{1/\alpha}\cdot{\mathrm{DIVERSITY}}=k\log P+1$ in Equation (4) based on the finding of the logarithmic trend. $\left(A,k,\alpha,E\right)$ are parameters to fit, and we use the natural logarithm (base e). We follow the fitting procedure from Hoffmann et al. (2022); Mu en nigh off et al. (2023), detailed in Appendix E.

我们假设在公式(4)中 $P^{1/\alpha}\cdot{\mathrm{DIVERSITY}}=k\log P+1$ ，这一假设基于对数趋势的发现。 $(A,k,\alpha,E)$ 是需要拟合的参数，我们使用自然对数(以e为底)。我们遵循Hoffmann等人(2022)和Muennighoff等人(2023)的拟合流程，具体细节见附录E。

Figure 2 illustrates the parallel scaling law fitted for two training datasets. It shows a high goodness of fit ( $\mathrm{\ddot{\Delta}R}^{2}$ up to 0.998), validating the effectiveness of Equation (5). Notably, we can observe that the $k$ value for Stack-V2 (0.39) is higher than for Pile (0.33). Recall that $k$ reflects the benefits of increased parallel computation. Since Stack-V2 emphasizes coding and reasoning abilities while Pile emphasizes memorization capacity, we propose an intuitive conjecture that model parameters mainly impact the memorization skills, while computation mainly impacts the reasoning skills. This aligns with recent findings on inference-time scaling (Geiping et al., 2025). Unlike those studies, we further quantitatively assess the ratio of contribution to model performance between parameters and computation through our proposed scaling laws.

图 2: 展示了针对两个训练数据集拟合的并行扩展规律。结果显示高拟合优度 ( $\mathrm{\ddot{\Delta}R}^{2}$ 最高达0.998) ，验证了公式(5) 的有效性。值得注意的是，Stack-V2的 $k$ 值(0.39) 高于Pile(0.33) 。回顾 $k$ 反映的是增加并行计算带来的收益。由于Stack-V2侧重编码和推理能力，而Pile侧重记忆能力，我们提出一个直观猜想：模型参数主要影响记忆技能，而计算量主要影响推理技能。这与近期关于推理时扩展的研究结论一致 (Geiping et al., 2025) 。不同于这些研究，我们进一步通过提出的扩展规律定量评估了参数和计算对模型性能的贡献比例。

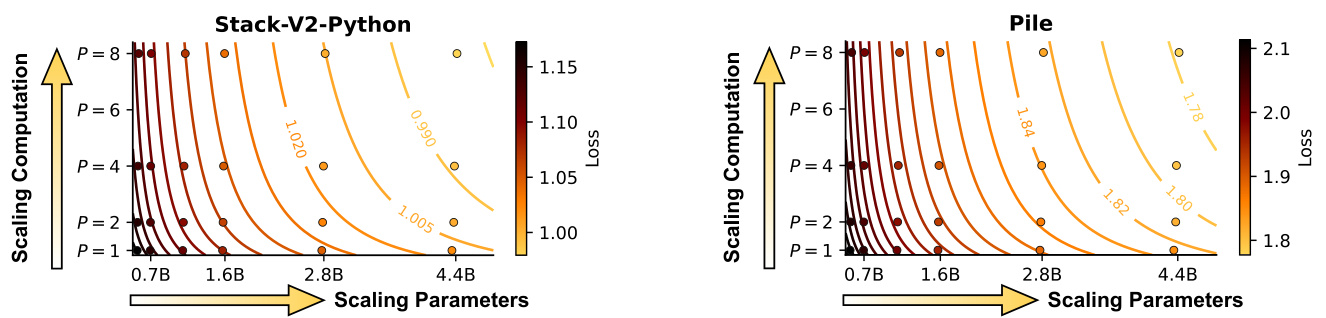
Figure 3: Predicted loss contours for PARSCALE. Each contour line indicates a combination of (parameter, $P$ ) with similar performance.

图 3: PARSCALE的预测损失等高线图。每条等高线表示一组具有相似性能的 (参数, $P$) 组合。

Table 2: Average performance $(%)$ on two code generation tasks, HumanEval $(+)$ and ${\mathrm{MBPP}}(+),$ after pre-training on the Stack-V2-Python dataset.

表 2: 在 Stack-V2-Python 数据集上预训练后，两个代码生成任务 HumanEval (+) 和 MBPP (+) 的平均性能 $(%)$。

N	0.5B	0.7B	1.1B	1.6B	2.8B	4.4B
P=1	26.7	28.4	31.6	33.9	36.9	39.2
P=2	30.3	32.4	33.6	37.4	39.4	42.6
P=4	30.1	32.5	34.1	37.6	40.7	42.6
P=8	32.3	34.0	37.2	39.1	42.1	45.4

Table 3: Average performance $(%)$ on six general lm-evaluation-harness tasks after pre-training on the Pile dataset.

表 3: 在 Pile 数据集上预训练后，六个通用 lm-evaluation-harness 任务的平均性能 $(%)$

N	0.5B	0.7B 1.1B		1.6B	2.8B	4.4B
P = 1	49.1	50.6	52.1	53.1	55.2	57.2
P = 2	49.9	51.0	52.4	54.4	57.0	58.5
P = 4	50.6	51.8	53.3	55.0	57.8	59.1
P = 8	50.7	51.8	54.2	55.7	58.1	59.6

Recall that Equation (5) implies scaling $P$ equates to increasing parameters by $\mathcal{O}(N\log P)$ . It suggests that models with more parameters benefit more from PARSCALE. Figure 3 more intuitively displays the influence of computation and parameters on model capacity. As model parameters increase, the loss contours flatten, showing greater benefits from increasing computation.

回想一下，式 (5) 表明缩放 $P$ 相当于将参数增加 $\mathcal{O}(N\log P)$ 。这表明参数更多的模型从 PARSCALE 中获益更大。图 3 更直观地展示了计算量和参数对模型能力的影响。随着模型参数增加，损失等高线趋于平缓，显示出增加计算量带来的更大收益。

Downstream Performance Tables 2 and 3 illustrate the average performance on downstream tasks (coding tasks for Stack-V2-Python and general tasks for Pile) after pre-training, with comprehensive results in Appendix G. It shows that increasing the number of parallel streams $P$ consistently boosts performance, which confirms that PARSCALE is able to enhance the model capabilities and similar to scale the parameters. Notably, PARSCALE offers more substantial improvements for coding tasks compared to general tasks. For example, as shown in Table 2, the coding ability of the 1.6B model for $P={\hat{8}}$ aligns with the 4.4B model, while Table 3 indicates that such setting performs comparably to the 2.8B model on general tasks that focusing on common-sense memorization. These findings affirm our previous hypothesis that the number of parameters impacts the memorization capacity, while computation impacts the reasoning capacity.

下游性能
表 2 和表 3 分别展示了预训练后在下游任务（Stack-V2-Python 的编程任务和 Pile 的通用任务）上的平均性能，完整结果见附录 G。结果表明，增加并行流数量 $P$ 能持续提升性能，这证实 PARSCALE 可以有效增强模型能力，其效果类似于扩大参数量。值得注意的是，与通用任务相比，PARSCALE 对编程任务的提升更为显著。例如，表 2 显示，当 $P={\hat{8}}$ 时，1.6B 模型的编程能力与 4.4B 模型相当；而表 3 表明，该设置在侧重常识记忆的通用任务上表现与 2.8B 模型相近。这些发现验证了我们先前的假设：参数量影响记忆能力，而计算量影响推理能力。

3.3 Inference Cost Analysis

3.3 推理成本分析

We further compare the inference efficiency between parallel scaling and parameter scaling at equivalent performance levels. Although some work uses FLOPS to measure the inference cost (Hoffmann et al., 2022; Sardana et al., 2024), we argue that this is not an ideal metric. Most Transformer operations are bottle necked by memory access rather than computation during the decoding stage (Ivanov et al., 2021). Some work (such as flash attention (Dao et al., 2022)) incurs more FLOPS but achieves lower latency by reducing memory access. Therefore, we use memory and latency to measure the inference cost, based on the llm-analysis framework (Li, 2023). Memory determines the minimum hardware requirements, while latency measures the time overhead from input to output.

我们进一步比较了在同等性能水平下并行扩展与参数扩展的推理效率差异。尽管部分研究采用FLOPS衡量推理成本 (Hoffmann et al., 2022; Sardana et al., 2024)，我们认为这并非理想指标——在解码阶段，大多数Transformer运算的瓶颈在于内存访问而非计算量 (Ivanov et al., 2021)。某些工作（如flash attention (Dao et al., 2022)）虽增加FLOPS，但通过减少内存访问实现了更低延迟。因此我们基于llm-analysis框架 (Li, 2023)，采用内存占用和延迟时间作为推理成本度量标准：内存决定最低硬件要求，延迟则衡量从输入到输出的时间开销。

We analyze the inference cost across various inference batch sizes. It is worth mentioning that all models in our experiments feature the same number of layers, differing only in parameter width and parallel streams (detailed in Appendix C). This enables a more fair comparison of the efficiencies.

我们分析了不同推理批次大小下的推理成本。值得一提的是，实验中所有模型的层数相同，仅在参数宽度和并行流数量上存在差异（详见附录C），这使得效率对比更加公平。

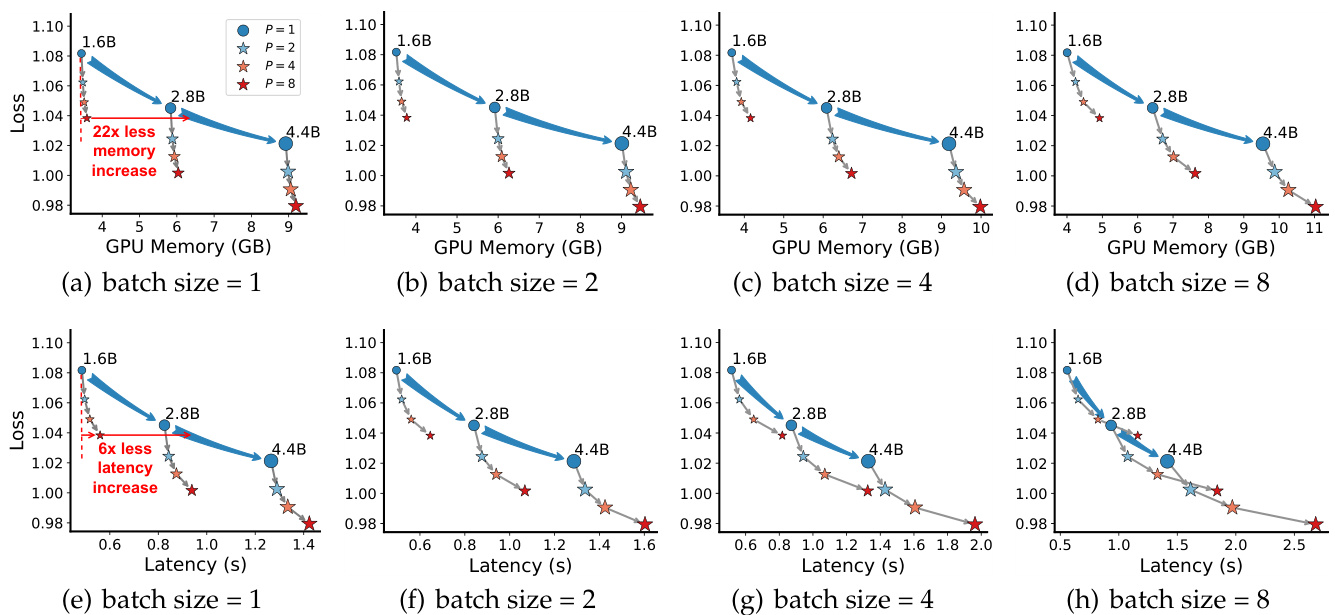
Figure 4: Model capacity (indicated by loss) scales on the inference space-time cost, with three parameters (1.6B, 2.8B, and 4.4B) and batch sizes $\in{1,2,4,8}$ . Results are averaged from input / output tokens $\in{64,128,256,512}$ . Blue arrows indicate parameter scaling; gray arrows represent parallel scaling.

图 4: 模型容量(以损失值表示)随推理时空成本的变化趋势，展示了三种参数量(1.6B/2.8B/4.4B)和批处理规模 $\in{1,2,4,8}$ 的关系。结果由输入/输出 tokens $\in{64,128,256,512}$ 的平均值得出。蓝色箭头表示参数量缩放，灰色箭头表示并行扩展。

Space Cost Figures 4(a) to 4(d) compare the inference memory usage of two scaling strategies, where we utilize loss on Stack-V2-Python as an indicator for model capacity. It shows that PARSCALE only marginally increases memory usage, even with larger batch sizes. This is because PARSCALE introduces negligible amounts of additional parameters (i.e., prefix tokens and aggregation weights, about $0.2%$ parameters per stream) and increases KV cache size (expanded by $\breve{P}$ times with $P$ streams), which generally occupies far less GPU memory than model parameters. As the input batch size increases, the KV cache size also grows; however, PARSCALE continues to demonstrate significantly better memory efficiency compared to parameter scaling. This suggests that PARSCALE maximizes the utility of memory through parameter reusing, while parameter scaling employs limited computation per parameter and cannot fully exploit computation resources.

空间成本
图4(a)至4(d)对比了两种扩展策略的推理内存占用情况，其中我们使用Stack-V2-Python数据集上的损失作为模型能力的指标。结果显示，即使批次规模增大，PARSCALE仅略微增加内存使用量。这是因为PARSCALE引入的额外参数量可忽略不计（即前缀token和聚合权重，每条流约占总参数的$0.2%$），同时增大的KV缓存（扩展为$\breve{P}$倍，共$P$条流）通常远少于模型参数占用的GPU内存。随着输入批次规模增大，KV缓存也会增长；但与参数扩展相比，PARSCALE始终展现出显著更优的内存效率。这表明PARSCALE通过参数复用最大化内存利用率，而参数扩展策略中每个参数的计算量有限，无法充分挖掘计算资源。

Time Cost Figures 4(e) to $4(\mathrm{h})$ compare the inference time of two scaling strategies. It shows that PARSCALE adds minimal latency at smaller batch sizes since the memory bottlenect is converted tothe computation bottleneck. Given that parallel computation introduced by PARSCALE is friendly to GPUs, it will not significantly raise latency. As batch sizes increase, decoding shifts from a memory to a computation bottleneck, resulting in higher costs for PARSCALE, but it remains more efficient than parameter scaling up to a batch size of 8.

时间成本 图 4(e) 到 $4(\mathrm{h})$ 比较了两种扩展策略的推理时间。结果表明，PARSCALE 在较小批量大小时增加的延迟极小，因为内存瓶颈被转化为计算瓶颈。鉴于 PARSCALE 引入的并行计算对 GPU 友好，它不会显著增加延迟。随着批量大小的增加，解码从内存瓶颈转变为计算瓶颈，导致 PARSCALE 的成本更高，但在批量大小达到 8 之前，它仍然比参数扩展更高效。

The above analysis indicates that PARSCALE is ideal for low-resource edge devices like smartphones, smart cars, and robots, where queries are typically few and batch sizes are small. Given limited memory resources in these environments, PARSCALE effectively utilizes memory and latency advantages at small batch sizes. When batch size is 1, for a 1.6B model and scaling to $\mathrm{P}\overset{\cdot}{=}8$ using PARSCALE, it uses $22\times$ less memory increase and $6\times$ less latency increase compared to parameter scaling that achieves the same performance. We anticipate that the future LLMs will gradually shift from centralized server deployments to edge deployments with the popularization of artificial intelligence. This suggests the promising potential of PARSCALE in the future.

上述分析表明，PARSCALE非常适合智能手机、智能汽车和机器人等资源有限的边缘设备，这些场景通常查询量少且批量较小。鉴于此类环境内存资源有限，PARSCALE能有效利用小批量下的内存和延迟优势。当批量大小为1时，对于16亿参数的模型，使用PARSCALE扩展到$\mathrm{P}\overset{\cdot}{=}8$的情况下，与达到相同性能的参数扩展方法相比，内存增量减少22倍，延迟增量降低6倍。我们预计，随着人工智能的普及，未来大语言模型将逐渐从集中式服务器部署转向边缘部署。这表明PARSCALE在未来具有广阔的应用前景。

4 Scaling Training Data

4 扩展训练数据

Due to our limited budget, our previous experiments on scaling laws focus on pre-training with 42 billion tokens. In this section, we will train a 1.8B model (with 1.6B non-embedding parameters) and scale the training data to 1T tokens, to investigate whether PARSCALE is effective for production-level training. We also apply PARSCALE to an off-the-shelf model, Qwen-2.5 (Qwen Team, 2024) (which is pre-trained on 18T tokens), under two settings: continual pre-training and parameter-efficient fine-tuning (PEFT).

由于预算有限，我们此前关于缩放定律的实验仅基于420亿token的预训练。本节将训练18亿参数模型（非嵌入参数16亿）并将训练数据扩展至1万亿token，以验证PARSCALE在生产级训练中的有效性。我们还在现成模型Qwen-2.5（Qwen Team, 2024）（预训练数据18万亿token）上应用PARSCALE，测试两种场景：持续预训练和参数高效微调（PEFT）。

Table 4: Performance comparison of the 1.8B models after training on 1T tokens from scratch using the two-stage strategy. We incorporate recent strong baselines (less than 2B parameters) as a comparison to validate that our $\mathrm{\Delta}P=1$ baseline is well-trained. The best performance and its comparable performance (within $0.5%$ ) is bolded. Appendix G elaborates the evaluation details. $@1$ : Pass $@1$ . $@10$ : Pass@10.

表 4: 采用两阶段策略从头训练 1T token 后 1.8B 模型的性能对比。我们引入近期强基线 (参数小于 2B) 进行对比，以验证 $\mathrm{\Delta}P=1$ 基线训练充分。最优性能及其可比性能 (误差在 $0.5%$ 内) 已加粗。附录 G 详述评估细节。$@1$: Pass@1, $@10$: Pass@10。

模型	Token	数据	平均	数学	代码	通用	MMLU	WinoGrande	Hellaswag	OBQA	PiQA	ARC
gemma-3-1B	2T	私有	53.4	1.9	14.9	26.4	61.4		63.0	37.8	75.6	56.2
Llama-3.2-1B	15T	私有	54.8	4.7	30.1	30.8	62.1		65.7	39.2	75.9	55.3
Qwen2.5-1.5B	18T	私有	63.6	52.3	55.8	61.0	65.6		68.0	42.6	76.6	67.9
SmolLM-1.7B	1T	公开	57.0	6.0	37.9	29.7	61.8		67.3	42.8	77.3	63.3
SmolLM2-1.7B	12T	公开	63.3	24.3	41.6	50.1	68.2		73.1	42.6	78.3	67.3
Baseline (P=1)	1T	公开	56.0	25.5	45.6	28.5	61.9		65.0	40.6	75.2	64.8
PARSCALE (P=2)	1T	公开	56.2	27.1	47.4	29.0	62.4		64.7	42.0	74.9	64.3
PARSCALE (P=4)	1T	公开	57.2	30.0	48.6	30.0	63.4		65.9	42.0	75.6	66.3
PARSCALE (P=8)	1T	公开	58.6	32.8 49.9	35.1	64.9		76.1	66.0

模型	Token	数据	GSM8K	GSM8K +CoT	Minerva Math	HumanEval @1	@10	HumanEval+ @1	@10	MBPP @1 @10	MBPP+ @1 @10
gemma-3-1B	2T	私有	1.8	2.3	1.5	6.7	15.9	6.1 14.6		13.0 29.1	10.8 23.0
Llama-3.2-1B	15T	私有	5.1	7.2	1.8	16.5	27.4	14.0 25.0	33.1	54.5	27.0 43.4
Qwen2.5-1.5B	18T	私有	61.7	67.2	28.1	36.0	62.8	31.1 55.5		61.9 79.6 66.4	50.8 68.5
SmolLM-1.7B	1T	公开	6.4	8.3	3.2	20.1	35.4	15.9 32.3		40.7 45.2	34.7 57.4
SmolLM2-1.7B	12T	公开	30.4	30.8	11.8	23.8	44.5	18.9 37.8		68.5	36.0 57.9
Baseline (P=1)	1T	公开	28.7	35.9	12.0	26.8	44.5	20.7 38.4		51.6 75.9	43.9 62.7
PARSCALE (P=2)	1T	公开	32.6	35.6	13.0	26.2	50.0	20.1 42.1		52.9 77.0	45.0 65.6
PARSCALE (P=4)	1T	公开	34.7	40.8	14.5	27.4	47.6	23.8 43.9		55.3 77.0	47.1 66.7
PARSCALE (P=8)	1T	公开	38.4	43.7	16.4	28.7	50.6	24.4 44.5		56.3 379.1	48.1 67.2

4.1 Two-Stage Pre training

4.1 两阶段预训练

While PARSCALE is efficient for the inference stage (as we discuss in Section 3.3), it still introduces about $P$ times of floating-point operations and significantly increases overhead in the computation-intensive training processes. To address this limitation, we propose a two-stage strategy: in the first stage, we use traditional pre-training methods with 1 trillion tokens; in the second stage, we conduct PARSCALE training with 20 billion tokens. Since the second stage accounts for only $2%$ of the first stage, this strategy can greatly reduce training costs. This two-stage strategy is similar to long-context fine-tuning (Ding et al., 2024), which also positions the more resource-intensive phase at the end. In this section, we will examine the effectiveness of this strategy.

虽然PARSCALE在推理阶段非常高效(如第3.3节所述)，但它仍会引入约$P$倍的浮点运算量，显著增加计算密集型训练过程的开销。为解决这一限制，我们提出两阶段策略：第一阶段使用传统预训练方法处理1万亿token；第二阶段采用PARSCALE训练200亿token。由于第二阶段仅占第一阶段的$2%$，该策略可大幅降低训练成本。这种两阶段策略类似于长上下文微调(Ding et al., 2024)，同样将资源消耗更大的阶段置于最后。本节我们将验证该策略的有效性。

Setup We follow Allal et al. (2025) and use the Warmup Stable Decay (WSD) learning rate schedule (Hu et al., 2024; Zhai et al., 2021). In the first stage, employing a 2K step warm-up followed by a fixed learning rate of 3e-4. In the second stage, the learning rate is annealed from 3e-4 to 1e-5. The rest of the hyper parameters remain consistent with the previous experiments (see Appendix C).

设置
我们遵循 Allal 等人的研究 [20]，采用 Warmup Stable Decay (WSD) 学习率调度策略 (Hu 等人 [21], Zhai 等人 [22])。第一阶段使用 2K 步的预热，随后固定学习率为 3e-4。第二阶段，学习率从 3e-4 退火至 1e-5。其余超参数与先前实验保持一致 (参见附录 C)。

In the first phase, we do not employ the PARSCALE technique. We refer to the recipe proposed by Allal et al. (2025) to construct our training data, which consists of 370B general data, 80B mathematics data, and 50B code data. We train the model for two epochs to consume 1T tokens. Among the general text, there are 345B from FineWeb-Edu (Penedo et al., 2024) and 28B from Cosmopedia 2 (Ben Allal et al., 2024); the mathematics data includes 80B from FineMath (Allal et al., 2025); and the code data comprises 47B from Stack-V2-Python and 4B from Stack-Python-Edu.

在第一阶段，我们不采用PARSCALE技术。我们参考Allal等人 (2025) 提出的方案构建训练数据，该数据集包含3700亿通用数据、800亿数学数据和500亿代码数据。我们训练模型两个周期以消耗1万亿token。其中通用文本包含3450亿来自FineWeb-Edu (Penedo等人, 2024) 和280亿来自Cosmopedia 2 (Ben Allal等人, 2024) 的数据；数学数据包含800亿来自FineMath (Allal等人, 2025) 的数据；代码数据包含470亿来自Stack-V2-Python语言和40亿来自Stack-Python-Edu的数据。

In the second phase, we use the trained model from the first phase as the backbone and introduce additional parameters from PARSCALE, which are randomly initialized using a standard deviation of 0.02 (based on the initialization of Qwen-2.5). Following (Allal et al., 2025), in this phase, we increase the proportion of mathematics and code data, finally including a total of 7B general text data, 7B mathematics data, and 7B Stack-Python-Edu data.

在第二阶段，我们使用第一阶段训练好的模型作为主干，并引入来自PARSCALE的额外参数，这些参数采用标准差为0.02进行随机初始化（基于Qwen-2.5的初始化方式）。根据 (Allal et al., 2025) 的研究，在此阶段我们提高了数学和代码数据的比例，最终包含总计70亿通用文本数据、70亿数学数据以及70亿Stack-Python-Edu数据。

Training Loss Figure 5 intuitively demonstrates the loss curve during our two-stage training. We find that at the beginning of the second phase, the loss for $P>1$ initially exceed those for $P=1$ due to the introduction of randomly initialized parameters. However, after processing a small amount of data (0.0002T tokens), the model quickly adapts to these newly introduced parameters and remains stable thereafter. This proves that PARSCALE can take effect rapidly with just a little data. We can also find that in the later stages, PARSCALE yields similar logarithmic gains. This aligns with previous scaling law findings, suggesting that our earlier conclusions for from-scratch pre-training — parallelism with $P$ streams equates to a ${\check{\mathcal{O}}}(N\log(P))$ increase in parameters — also applies to continued pre training. Additionally, larger $P$ (such as $P=8$ ) can gradually widen the gap compared to smaller $P$ values (such as $P=4^{\cdot}$ ). This demonstrates that parallel scaling can also benefit from data scaling.

训练损失
图 5 直观展示了两阶段训练过程中的损失曲线。我们发现，在第二阶段初期，由于引入随机初始化参数，$P>1$ 的损失值会暂时超过 $P=1$ 的情况。但在处理少量数据（0.0002T tokens）后，模型迅速适应新增参数并保持稳定。这证明 PARSCALE 仅需极少量数据即可快速生效。后期阶段中，PARSCALE 产生了相似的对数级收益，这与先前扩展律的研究结论一致，表明我们关于从零开始预训练的结论——$P$ 路并行等价于参数增加 ${\check{\mathcal{O}}}(N\log(P))$——同样适用于持续预训练。此外，较大 $P$ 值（如 $P=8$）相比小 $P$ 值（如 $P=4^{\cdot}$）会逐渐拉开差距，说明并行扩展也能从数据扩展中获益。

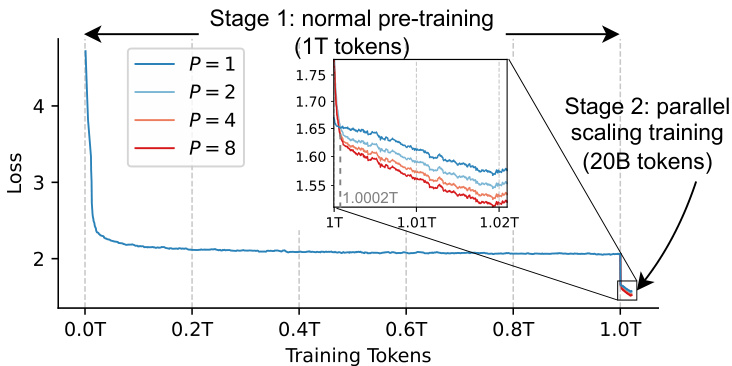
Figure 5: Loss for two-stage training, smoothing using an exponential moving average with a weight of 0.95.

图 5: 两阶段训练的损失函数，采用权重为0.95的指数移动平均进行平滑处理。

Table 5: Comparison of the performance of different Instruct models, where the few-shot examples are treated as a multi-turn conversation.

表 5: 不同Instruct模型性能对比，其中少样本示例被视为多轮对话。

	IFEval MMLU 零样本 5样本	GSM8K 4样本
SmolLM-1.7B-Inst	16.3 28.4	2.0
Baseline-Inst (P=1)	54.1 34.2	50.3
PARSCALE-Inst (P=2)	55.8 35.1	55.3
PARSCALE-Inst (P=4)	58.4 38.2	54.8
PARSCALE-Inst (P=8)	59.5 41.7	56.1

Downstream Performance In Table 4, we report the downstream performance of the model after finishing two-stage training, across 7 general tasks, 3 math tasks, and 8 coding tasks. It can be observed that with the increase of $P$ , the performance presents an upward trend for most of the benchmarks, which validates the effectiveness of PARSCALE trained on the large dataset. Specifically, when $P$ increases from 1 to 8, PARSCALE improves by $2.6%$ on general tasks, and by $7.3%$ and $4.3%$ on math and code tasks, respectively. It achieves a $10%$ improvement $34%$ relative improvement) on GSM8K. This reaffirms that PARSCALE can more effectively address reasoning-intensive tasks. Moreover, in combination with CoT, it achieves about an $8%$ improvement on GSM8K, suggesting that parallel scaling can be used together with inference-time scaling to achieve better results. Compared to the SmolLM-1.7B model, which was also trained on 1T tokens, our $P=1$ baseline achieves comparable results on general tasks and significantly outperforms on math and code tasks. One explanation is that SmolLM training set focuses more on commonsense and world knowledge corpus, while lacking high-quality math and code data. This validates the effectiveness of our dataset construction and training strategy, and further enhances the credibility of our experimental results.

下游性能

在表4中，我们报告了模型完成两阶段训练后在7个通用任务、3个数学任务和8个编程任务上的下游性能。可以观察到，随着$P$值的增加，大多数基准测试的性能呈现上升趋势，这验证了在大规模数据集上训练的PARSCALE的有效性。具体而言，当$P$从1增加到8时，PARSCALE在通用任务上提升了$2.6%$，在数学和编程任务上分别提升了$7.3%$和$4.3%$。在GSM8K上实现了$10%$的绝对提升（相对提升$34%$），这再次证实PARSCALE能更有效地解决推理密集型任务。此外，结合思维链(CoT)技术，模型在GSM8K上实现了约$8%$的提升，表明并行缩放可以与推理时缩放技术结合使用以获得更好效果。与同样训练了1T token的SmolLM-1.7B模型相比，我们的$P=1$基线在通用任务上取得了相当的结果，而在数学和编程任务上显著优于前者。一个可能的解释是SmolLM的训练集更侧重于常识和世界知识语料，而缺乏高质量的数学和编程数据。这验证了我们数据集构建和训练策略的有效性，并进一步增强了实验结果的可靠性。

Instruction Tuning We follow standard practice to post-train the base models, to explore whether PARSCALE can enhance performance during the post-training stage. We conducted instruction tuning on four checkpoints $(P\in{1,2,4,8})$ from the previous pre-training step, increasing the sequence length from 2048 to 8192 and the RoPE base from 10,000 to 100,000, while keeping other hyper parameters constant. We used 1 million SmolTalk (Allal et al., 2025) as the instruction tuning data and trained for 2 epochs. We refer to these instruction models as PARSCALE-Inst.

指令微调
我们遵循标准实践对基础模型进行后训练，以探究PARSCALE能否在后训练阶段提升性能。我们在预训练阶段的四个检查点$(P\in{1,2,4,8})$上进行指令微调，将序列长度从2048增至8192，并将RoPE基数从10,000调整至100,000，同时保持其他超参数不变。我们使用100万条SmolTalk (Allal et al., 2025)数据作为指令微调数据集，训练2个周期。这些经过指令微调的模型称为PARSCALE-Inst。

The experimental results in Table 5 show that when $P$ increases from 1 to 8, our method achieves a $5%$ improvement on the instruction-following benchmark IFEval, along with substantial gains in the general task MMLU and the reasoning task GSM8K. This demonstrates that the proposed PARSCALE performs effectively during the post-training phase.

表 5 中的实验结果表明，当 $P$ 从 1 增加到 8 时，我们的方法在指令跟随基准 IFEval 上实现了 $5%$ 的提升，同时在通用任务 MMLU 和推理任务 GSM8K 上也取得了显著进步。这表明所提出的 PARSCALE 在后训练阶段表现高效。

4.2 Applying to the Off-the-Shelf Pre-Trained Model

4.2 应用于现成的预训练模型

We further investigate applying PARSCALE to off-the-shelf models under two settings: continual pretraining and parameter-efficient fine-tuning (PEFT). Specifically, we use Pile and Stack-V2 (Python) to continue pre-training the Qwen-2.5 (3B) model. The training settings remain consistent with Appendix C, with the only difference being that we initialize with Qwen2.5-3B weights and adjust the RoPE base to the preset 1,000,000.

我们进一步研究了在持续预训练和参数高效微调 (PEFT) 两种设置下将 PARSCALE 应用于现成模型的效果。具体而言，我们使用 Pile 和 Stack-V2 (Python语言) 对 Qwen-2.5 (3B) 模型进行持续预训练。训练设置与附录 C 保持一致，唯一区别在于我们使用 Qwen2.5-3B 权重进行初始化，并将 RoPE base 调整为预设值 1,000,000。

Continual Pre-Training Figures 6(a) and $6(\mathrm{b})$ illustrates the training loss after continuous pre-training on Stack-V2 (Python) and Pile. Notably, Qwen2.5 has already been pre-trained on 18T of data, which possibly have significant overlap with both Pile and Stack-V2. This demonstrates that improvements can still be achieved even with a thoroughly trained foundation model and commonly used training datasets.

持续预训练
图 6(a) 和 $6(\mathrm{b})$ 展示了在 Stack-V2 (Python语言) 和 Pile 数据集上持续预训练后的损失曲线。值得注意的是，Qwen2.5 已在 18T 数据上完成预训练，这些数据很可能与 Pile 和 Stack-V2 存在显著重叠。这表明即使基础模型经过充分训练且使用常见训练数据集，仍能实现性能提升。

Parameter-Efficient Fine-Tuning We further utilize PEFT to fine-tune the introduced parameters while freezing the backbone weights. Figure 6(c) shows that this strategy can still significantly improve downstream code generation performance. Moreover, this demonstrates the promising prospects of dynamic parallel scaling: we can deploy the same backbone and flexibly switch between different numbers of parallel streams in various scenarios (e.g., high throughput and low throughput), which enables quick transitions between different levels of model capacities.

参数高效微调 (Parameter-Efficient Fine-Tuning)
我们进一步利用PEFT对引入的参数进行微调，同时冻结主干网络权重。图6(c)显示该策略仍能显著提升下游代码生成性能。此外，这证明了动态并行扩展的广阔前景：我们可以部署相同的主干网络，在不同场景(如高吞吐和低吞吐)中灵活切换并行流数量，从而实现不同级别模型容量的快速切换。

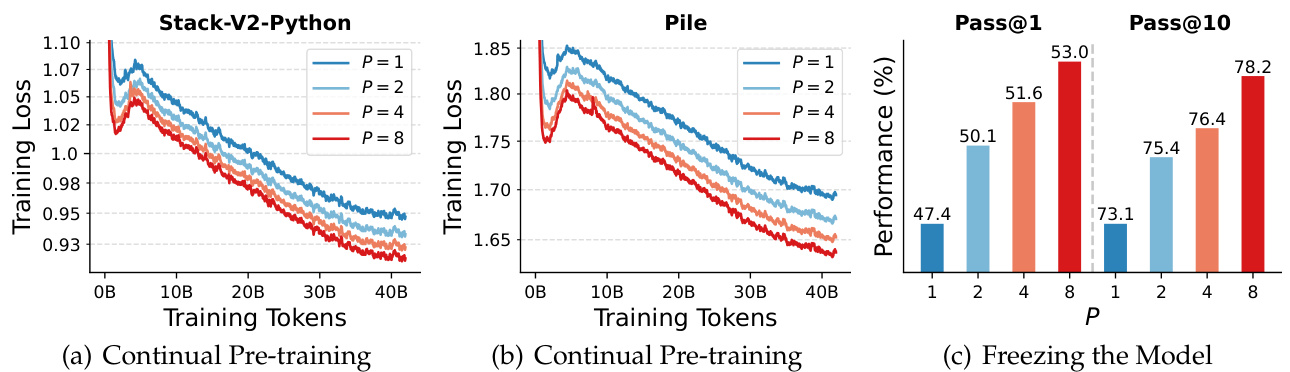
Figure 6: (a)(b) Loss for continual pre-training the Qwen-2.5-3B model on the two datasets. (c) Code generation performance after fine-tuning on Stack-V2 (Python), averaged from HumanEval $(+)$ and $\mathrm{{\check{M}B P P}}(+)$ . We only fine-tune the introduced parameters (prefix tokens and aggregation weights), with different $P$ sharing exactly the same Qwen2.5-3B pre-trained weights.

图 6: (a)(b) Qwen-2.5-3B模型在两个数据集上持续预训练的损失。(c) 在Stack-V2 (Python语言)微调后的代码生成性能，取HumanEval $(+)$ 和 $\mathrm{{\check{M}B P P}}(+)$ 的平均值。我们仅微调引入的参数(前缀token和聚合权重)，不同 $P$ 共享完全相同的Qwen2.5-3B预训练权重。

5 Related Work

5 相关工作

Beyond language modeling, our work can be connected to various machine learning domains. First, scaling computation while maintaining parameters is also the core idea of inference-time scaling. Second, as previously mentioned, PARSCALE can be viewed as a dynamic and scalable classifier-free guidance. Third, our method can be seen as a special case of model ensemble. Lastly, the parallel scaling law we explore is a generalization of the existing language model scaling laws.

除了语言建模，我们的工作还可以与多个机器学习领域相关联。首先，在保持参数不变的情况下扩展计算量也是推理时扩展 (inference-time scaling) 的核心思想。其次，如前所述，PARSCALE 可视为一种动态且可扩展的无分类器引导 (classifier-free guidance) 方法。第三，我们的方法可视为模型集成 (model ensemble) 的一种特例。最后，我们探索的并行扩展定律是对现有大语言模型扩展定律的广义推广。

Inference-Time Scaling The notable successes of reasoning models, such as GPT-o1 (OpenAI, 2024), DeepSeek-R1 (DeepSeek-AI, 2025), QwQ (Qwen Team, 2025a), and Kimi k1.5 (Kimi Team, 2025) have heightened interest in inference-time scaling. These lines of work (Wei et al., 2022; Madaan et al., 2023; Zhou et al., 2023a) focus on scaling serial computation to increase the length of the chain-of-thought (Wei et al., 2022). Despite impressiveness, it results in inefficient inference and sometimes exhibits over thinking problems (Chen et al., 2024b; Sui et al., 2025).

推理时扩展
GPT-o1 (OpenAI, 2024)、DeepSeek-R1 (DeepSeek-AI, 2025)、QwQ (Qwen Team, 2025a) 和 Kimi k1.5 (Kimi Team, 2025) 等推理模型的显著成功，引发了人们对推理时扩展的浓厚兴趣。这些研究工作 (Wei et al., 2022; Madaan et al., 2023; Zhou et al., 2023a) 侧重于扩展串行计算以增加思维链 (Wei et al., 2022) 的长度。尽管效果令人印象深刻，但它会导致推理效率低下，有时还会表现出过度思考的问题 (Chen et al., 2024b; Sui et al., 2025)。

Other lines of approaches focus on scaling parallel computation. Early methods such as beam search (Wiseman & Rush, 2016), self-consistency (Wang et al., 2023b), and majority voting (Chen et al., 2024a) require no additional training. We also provide an experimental comparison with Beam Search in Appendix H, which shows the importance of scaling parallel computing during the training stage. Recently, the proposal-verifier paradigm has gained attention, by employing a trained verifier to select from multiple parallel outputs (Brown et al., 2024; Wu et al., 2025; Zhang et al., 2024b). However, these methods are limited to certain application scenarios (i.e., generation tasks) and specialized training data (i.e., reward signals).

其他研究方向聚焦于扩展并行计算。早期方法如束搜索 (beam search) (Wiseman & Rush, 2016)、自洽性 (self-consistency) (Wang et al., 2023b) 和多数投票 (majority voting) (Chen et al., 2024a) 无需额外训练。我们还在附录 H 中提供了与束搜索的实验对比，结果表明训练阶段扩展并行计算的重要性。近期，提案-验证范式 (proposal-verifier paradigm) 通过训练验证器从多个并行输出中选择 (Brown et al., 2024; Wu et al., 2025; Zhang et al., 2024b) 而受到关注，但这些方法仅适用于特定应用场景 (即生成任务) 和专用训练数据 (即奖励信号)。

More recently, Geiping et al. (2025) introduce training LLMs to reason within the latent space and scale sequential computation, applicable to any application scenarios without needing specialized datasets. However, this method demands significant serial computation scaling (e.g., 64 times the looping) and invasive model modifications, necessitating training from scratch and complicating integration with existing trained LLMs.

近期，Geiping等人 (2025) 提出了一种训练大语言模型 (LLM) 在潜在空间中进行推理并扩展序列计算的方法，该方法无需专用数据集即可适用于任何应用场景。然而，这种方法需要大量的串行计算扩展 (例如64倍循环) 和侵入式的模型修改，必须从头开始训练，并且难以与现有训练好的大语言模型集成。

Classifier-Free Guidance Classifier-Free Guidance (CFG) stems from Classifier Guided Diffusion (Dhariwal & Nichol, 2021), which uses an additional classifier to guide image generation using diffusion models (Ho et al., 2020). By using the generation model itself as a classifier, CFG (Ho & Salimans, 2022) further eliminates dependency on the classifier and leverage two forward passes. Similar concepts have emerged in NLP, such as Coherence Boosting (Malkin et al., 2022), PREADD (Pei et al., 2023), ContextAware Decoding (Shi et al., 2024), and Contrastive Decoding (Li et al., 2023). Recently, Sanchez et al. (2024) proposed transferring CFG to language models. However, due to constraints of human-designed heuristic rules, these techniques cannot leverage the power of training-time scaling (Kaplan et al., 2020) and the performance is limited.

无分类器引导 (Classifier-Free Guidance, CFG) 源自分类器引导扩散模型 (Classifier Guided Diffusion) [Dhariwal & Nichol, 2021]，该方法通过额外分类器指导扩散模型 (diffusion models) [Ho et al., 2020] 的图像生成。CFG [Ho & Salimans, 2022] 利用生成模型自身作为分类器，进一步消除对分类器的依赖，并通过两次前向计算实现引导。类似概念在自然语言处理领域相继出现，例如一致性增强 (Coherence Boosting) [Malkin et al., 2022]、PREADD [Pei et al., 2023]、上下文感知解码 (ContextAware Decoding) [Shi et al., 2024] 以及对比解码 (Contrastive Decoding) [Li et al., 2023]。近期 Sanchez 等人 [2024] 提出将 CFG 迁移至语言模型，但由于人工设计启发式规则的局限性，这些技术无法充分发挥训练时扩展 (training-time scaling) [Kaplan et al., 2020] 的潜力，性能存在上限。

Model Ensemble Model ensemble is a classic research field in machine learning and is also employed in the context of LLMs (Chen et al., 2025). In traditional model ensembles, most ensemble components do not share parameters. Some recent work consider setups with partially shared parameters. For example, Monte Carlo dropout (Gal & Ghahramani, 2016) employs multiple different random dropouts during the inference phase, while Batch Ensemble (Wen et al., 2020; Tran et al., 2022) and LoRA ensemble (Wang et al., 2023a) use distinct low-rank matrix factorization s for model weights to differentiate different streams (we also experimented with this technique as input transformation in Appendix A). Weight sharing (Yang et al., 2021; Lan et al., 2019) is another line of work, where some weights of a model are shared across different components and participate in multiple computations. However, these works have not explored the scaling law of parallel computation from the perspective of model capacity. As we discuss in Appendix A, we find that the specific differentiation technique had a minimal impact, and the key factor is the scaling in parallel computation.

模型集成
模型集成是机器学习中的经典研究领域，也被应用于大语言模型 (Chen et al., 2025)。在传统模型集成中，大多数集成组件不共享参数。近期部分研究探索了参数部分共享的配置，例如蒙特卡洛dropout (Gal & Ghahramani, 2016) 在推理阶段采用多种不同的随机丢弃策略，而批集成 (Wen et al., 2020; Tran et al., 2022) 和LoRA集成 (Wang et al., 2023a) 则通过不同的低秩矩阵分解方式区分模型权重流 (我们在附录A中也尝试将该技术作为输入变换)。权重共享 (Yang et al., 2021; Lan et al., 2019) 是另一类研究方向，即模型的某些权重在不同组件间共享并参与多次计算。但这些工作尚未从模型容量的角度探索并行计算的缩放规律。如附录A所述，我们发现具体区分技术的影响微乎其微，关键因素在于并行计算的规模扩展。

Scaling Laws for Language Models Many researchers explore the predictable relationships between LLM training performance and various factors under different settings, such as the number of parameters and data (Hestness et al., 2017; Kaplan et al., 2020; Hoffmann et al., 2022; DeepSeek-AI, 2024; Frantar et al., 2024), data repetition cycles (Mu en nigh off et al., 2023; Hernandez et al., 2022), data mixing (Ye et al., 2025; Que et al., 2024), and fine-tuning (Zhang et al., 2024a). By extending the predictive empirical scaling laws developed from smaller models to larger models, we can significantly reduce exploration costs. Recently, some studies have investigated the scaling effects during inference (Sardana et al., 2024), noting a log-linear relationship between sampling number and performance (Brown et al., 2024; Snell et al., 2025). But they are limited to certain application scenarios. Our work extends the Chinchilla scaling law (Hoffmann et al., 2022) by introducing the intrinsic quantitative relationship between parallel scaling and parameter scaling. Existing literature has also identified a power-law relationship between the number of ensembles and loss in model ensemble scaling laws (Lobacheva et al., 2020a), which can be considered a special case of Proposition 1 when $\rho=0$ .

大语言模型的扩展规律
许多研究者探索了大语言模型(LLM)训练性能与不同设置下各因素之间的可预测关系，例如参数量与数据量 (Hestness et al., 2017; Kaplan et al., 2020; Hoffmann et al., 2022; DeepSeek-AI, 2024; Frantar et al., 2024)、数据重复周期 (Mu en nigh off et al., 2023; Hernandez et al., 2022)、数据混合 (Ye et al., 2025; Que et al., 2024) 以及微调 (Zhang et al., 2024a)。通过将从小型模型总结的预测性经验扩展规律延伸至大型模型，我们能显著降低探索成本。近期部分研究开始关注推理阶段的扩展效应 (Sardana et al., 2024)，发现采样数量与性能呈对数线性关系 (Brown et al., 2024; Snell et al., 2025)，但这些发现仅适用于特定应用场景。我们的工作通过引入并行扩展与参数扩展之间的内在量化关系，扩展了Chinchilla扩展规律 (Hoffmann et al., 2022)。现有文献还发现模型集成扩展规律中集成数量与损失之间存在幂律关系 (Lobacheva et al., 2020a)，这可以视为命题1在 $\rho=0$ 时的特例。

6 Discussion and Future Work

6 讨论与未来工作

Training Inference-Optimal Language Models Chinchilla (Hoffmann et al., 2022) explored the scaling law to determine the training-optimal amounts for parameters and training data under a training FLOP budget. On the other hands, modern LLMs are increasingly interested on inference-optimal models. Some practitioners use much more data than the Chinchilla recommendation to train small models due to their high inference efficiency (Qwen Team, 2024; Allal et al., 2025; Sardana et al., 2024). Recent inference-time scaling efforts attempt to provide a computation-optimal strategy during the inference phase (Wu et al., 2025; Snell et al., 2025), but most rely on specific scenarios and datasets. Leveraging the proposed PARSCALE, determining how to allocate the number of parameters and parallel computation under various inference budgets (e.g., memory, latency, and batch size) to extend inference-optimal scaling laws (Sardana et al., 2024) is a promising direction.

训练推理最优的语言模型
Chinchilla (Hoffmann et al., 2022) 探索了缩放定律，以确定在给定训练 FLOP 预算下参数和训练数据的最优训练量。另一方面，现代大语言模型越来越关注推理最优的模型。由于推理效率高，一些实践者使用远超 Chinchilla 建议的数据量来训练小模型 (Qwen Team, 2024; Allal et al., 2025; Sardana et al., 2024)。最近的推理时缩放研究尝试在推理阶段提供计算最优策略 (Wu et al., 2025; Snell et al., 2025)，但大多依赖于特定场景和数据集。利用提出的 PARSCALE，确定如何在不同的推理预算 (如内存、延迟和批量大小) 下分配参数数量和并行计算，以扩展推理最优缩放定律 (Sardana et al., 2024)，是一个有前景的方向。

Further Theoretical Analysis for Parallel Scaling Laws One of our contributions is quantitatively computing the impact of parameters and computation on model capability. Although we present some theoretical results (Proposition 1), the challenge of directly modeling DIVERSITY limits us to using extensive experiments to fit parallel scaling laws. Why the diversity is related to ${\log}P,$ is there a growth rate that exceeds $\mathcal{O}(\log P)$ , and whether there is a performance upper bound for $\bar{P}\gg8$ , remain open questions.

并行扩展定律的进一步理论分析

我们的贡献之一是定量计算参数和计算对模型能力的影响。尽管我们提出了一些理论结果 (Proposition 1)，但直接建模 DIVERSITY 的挑战迫使我们通过大量实验来拟合并行扩展定律。为何多样性会与 ${\log}P$ 相关、是否存在超过 $\mathcal{O}(\log P)$ 的增长率，以及当 $\bar{P}\gg8$ 时是否存在性能上限，这些问题仍有待探索。

Optimal Division Point of Two-Stage Strategy Considering that PARSCALE is inefficient in the training phase, we introduced a two-stage strategy and found that LLMs can still learn to leverage parallel computation for better capacity with relatively few tokens. We currently employ a 1T vs. 20B tokens as the division point. Whether there is a more optimal division strategy and its trade-off with performance is also an interesting research direction.

考虑PARSCALE在训练阶段效率较低的问题，我们引入两阶段策略并发现大语言模型(LLM)仍能通过相对较少的token学习利用并行计算来提升能力。当前采用1T与20B tokens作为分界点，是否存在更优划分策略及其与性能的权衡也是值得研究的方向。

Application to MoE Architecture Similar to the method proposed by Geiping et al. (2025), PARSCALE is a computation-heavy (but more efficient) strategy. This is somewhat complementary to sparse MoE (Fedus et al., 2022; Shazeer et al., 2017), which is parameter-heavy. Considering that MoE is latencyfriendly while PARSCALE is memory-friendly, exploring whether their combination can yield more efficient and high-performing models is worth investigating.

应用于MoE架构
与Geiping等人 (2025) 提出的方法类似，PARSCALE是一种计算密集型（但更高效）的策略。这与参数密集型的稀疏MoE (Fedus等人, 2022; Shazeer等人, 2017) 形成一定互补。考虑到MoE对延迟友好而PARSCALE对内存友好，探索二者结合能否产生更高效、更高性能的模型值得研究。

Application to Other Machine Learning Domains Although we focus on language models, PARSCALE is a more general method that can be applied to any model architecture, training algorithm, and training data. Exploring PARSCALE in other areas and even proposing new scaling laws is also a promising direction for the future.

应用于其他机器学习领域
尽管我们专注于语言模型，但PARSCALE是一种更通用的方法，可应用于任何模型架构、训练算法和训练数据。在其他领域探索PARSCALE甚至提出新的扩展定律也是未来一个很有前景的方向。

7 Conclusions

7 结论

In this paper, we propose a new type of scaling strategy, PARSCALE, for training LLMs by reusing existing parameters for multiple times to scale the parallel computation. Our theoretical analysis and extensive experiments propose a parallel scaling law, showing that a model with $N$ parameters and $P\times$ parallel computation can be comparable to a model with $\mathcal{O}(\breve{N}\log{P})$ parameters. We scale the training data to 1T tokens to validate PARSCALE in the real-world practice based on the proposed two-stage strategy, and show that PARSCALE remains effective with frozen main parameters for different $P$ . We also demonstrate that parallel scaling is more efficient than parameter scaling during the inference time, especially in low-resource edge scenarios. As artificial intelligence becomes increasingly widespread, we believe that future LLMs will progressively transition from centralized server deployments to edge deployments, and PARSCALE could emerge as a promising technique for these scenarios.

本文提出了一种新型扩展策略PARSCALE，通过重复利用现有参数实现并行计算的多次扩展来训练大语言模型。我们的理论分析和大量实验提出了一条并行扩展定律：具有$N$个参数和$P\times$并行计算的模型，其性能可与具有$\mathcal{O}(\breve{N}\log{P})$个参数的模型相媲美。基于提出的两阶段策略，我们将训练数据扩展到1T token以验证PARSCALE在实际应用中的有效性，结果表明在不同$P$值下冻结主要参数时PARSCALE仍保持优势。我们还证明了在推理阶段，尤其是边缘低资源场景中，并行扩展比参数扩展更具效率。随着人工智能的普及，我们相信未来大语言模型将逐渐从集中式服务器部署转向边缘部署，而PARSCALE有望成为这些场景的关键技术。

Acknowledgement

致谢

This research is partially supported by Zhejiang Provincial Natural Science Foundation of China (No. LZ 25 F 020003) and the National Natural Science Foundation of China (No. 62202420). The authors would like to thank Jiquan Wang, Han Fu, Zhiling Luo, and Yusu Hong for their early idea discussions and inspirations, as well as Lingzhi Zhou for the discussions on efficiency analysis.

本研究部分得到浙江省自然科学基金 (No. LZ25F020003) 和国家自然科学基金 (No. 62202420) 的资助。作者感谢王继全、傅涵、罗志玲和洪雨素在早期想法讨论与灵感启发方面的贡献，以及周凌志在效率分析方面的探讨。

References

参考文献

Leo Breiman. Random forests. Mach. Learn., 45(1):5–32, October 2001. ISSN 0885-6125. doi: 10.1023/A: 1010933404324. URL https://doi.org/10.1023/A:1010933404324.

Leo Breiman. 随机森林 (Random Forests). Mach. Learn., 45(1):5–32, 2001年10月. ISSN 0885-6125. doi: 10.1023/A:1010933404324. URL https://doi.org/10.1023/A:1010933404324.

Bradley Brown, Jordan Juravsky, Ryan Ehrlich, Ronald Clark, Quoc V. Le, Christopher Ré, and Azalia Mirhoseini. Large language monkeys: Scaling inference compute with repeated sampling. arXiv preprint arXiv:2407.21787, 2024. URL https://arxiv.org/abs/2407.21787.

Bradley Brown、Jordan Juravsky、Ryan Ehrlich、Ronald Clark、Quoc V. Le、Christopher Ré 和 Azalia Mirhoseini。大语言模型猴子：通过重复采样扩展推理计算。arXiv预印本 arXiv:2407.21787，2024。URL https://arxiv.org/abs/2407.21787。

Andrei Ivanov, Nikoli Dryden, Tal Ben-Nun, Shigang Li, and Torsten Hoefler. Data movement is all you need: A case study on optimizing transformers. In A. Smola, A. Dimakis, and I. Stoica (eds.), Proceedings of Machine Learning and Systems, volume 3, pp. 711–732, 2021. URL https://proceedings. mlsys.org/paper files/paper/2021/file/bc 86 e 95606 a 6392 f 51 f 95 a 8 de 106728 d-Paper.pdf.

Andrei Ivanov、Nikoli Dryden、Tal Ben-Nun、Shi