Exploiting Local Geometry for Feature and Graph Construction for Better 3D Point Cloud Processing with Graph Neural Networks
利用局部几何特征和图结构优化基于图神经网络的3D点云处理
Abstract— We propose simple yet effective improvements in point representations and local neighborhood graph construction within the general framework of graph neural networks (GNNs) for 3D point cloud processing. As a first contribution, we propose to augment the vertex representations with important local geometric information of the points, followed by nonlinear projection using a MLP. As a second contribution, we propose to improve the graph construction for GNNs for 3D point clouds. The existing methods work with a $k$ -NN based approach for constructing the local neighborhood graph. We argue that it might lead to reduction in coverage in case of dense sampling by sensors in some regions of the scene. The proposed methods aims to counter such problems and improve coverage in such cases. As the traditional GNNs were designed to work with general graphs, where vertices may have no geometric interpretations, we see both our proposals as augmenting the general graphs to incorporate the geometric nature of 3D point clouds. While being simple, we demonstrate with multiple challenging benchmarks, with relatively clean CAD models, as well as with real world noisy scans, that the proposed method achieves state of the art results on benchmarks for 3D classification (ModelNet40) , part segmentation (ShapeNet) and semantic segmentation (Stanford 3D Indoor Scenes Dataset). We also show that the proposed network achieves faster training convergence, i.e. $\sim40%$ less epochs for classification. The project details are available at https://siddha rth sri vast ava. github.io/publication/geomgcnn/
摘要—我们在用于3D点云处理的图神经网络(GNN)通用框架中,提出了简单而有效的点表示方法和局部邻域图构建改进方案。首先,我们提出通过加入点的关键局部几何信息来增强顶点表示,随后使用多层感知机(MLP)进行非线性投影。其次,我们改进了3D点云的GNN图构建方法。现有方法采用基于k近邻($k$-NN)的局部邻域图构建策略,我们认为在场景某些区域存在传感器密集采样时,这可能导致覆盖范围缩减。所提方法旨在解决此类问题并提升覆盖率。由于传统GNN设计初衷是处理无几何特性的通用图结构,我们将这两项改进视为对通用图的几何特性增强,以适应3D点云的几何本质。尽管方法简洁,但我们在多个具有挑战性的基准测试中(包括相对干净的CAD模型和真实噪声扫描数据)证明,所提方法在3D分类(ModelNet40)、部件分割(ShapeNet)和语义分割(Stanford 3D室内场景数据集)基准上达到了最先进水平。实验还表明该网络能实现更快的训练收敛,分类任务所需训练轮次减少约40%。项目详情见https://siddha rth sri vast ava. github.io/publication/geomgcnn/
I. INTRODUCTION
I. 引言
Significant progress has been made recently towards designing neural network architectures for directly processing unstructured 3D point clouds [1]. Since 3D point clouds are obtained as the native output from commonly available scanning sensors, the ability to process them and apply machine learning methods directly to them is interesting, and allows for many useful applications [2]. Like many other input modalities, both handcrafted and learning based methods are available for extracting meaningful information from 3D point clouds. The current state-of-the-art techniques for extracting such information are mostly based on deep neural networks.
近期在直接处理非结构化3D点云的神经网络架构设计方面取得了重大进展[1]。由于3D点云是常见扫描传感器的原生输出数据,直接对其进行处理并应用机器学习方法具有重要价值,可实现多种实用应用[2]。与其他输入模态类似,从3D点云提取有效信息既可采用人工设计方法,也可使用基于学习的方法。当前最先进的信息提取技术主要基于深度神经网络。
As the point clouds are unordered, it is difficult to use CNNs with them. The popular ways of overcoming the problem of unstructured point clouds have been to either (i) voxelize them, e.g. [3] or (ii) learn a permutation invariant mapping, e.g. [4]. Point clouds can also be seen as graphs with potential edges defined between neighboring points. Therefore, utilizing graph neural networks (GNN) for processing point cloud data emerges as a natural choice. Most of the earlier GNN methods [5] considered the points in isolation, and did not explicitly utilize the information from local neighborhoods. While such local geometric information can be helpful for higher level tasks, these methods expected the network to learn the important intricacies directly from isolated points as inputs. However, the Dynamic EdgeConv network [6] showed that local geometric properties are important for learning feature representations from point clouds. They proposed to use the differences between the 3D points and their neighbors, which can be interpreted as a 3D direction vector, to encode the local structure. In addition, they converted the point cloud to a graph using a $k$ -NN based construction, which is another way of encoding local geometric structure for use by the method. By doing this they were able to close the gap between GNN based methods and other state-of-the-art point cloud processing methods.
由于点云是无序的,很难对其使用CNN。解决非结构化点云问题的流行方法包括:(i) 体素化处理 [3] ,或 (ii) 学习置换不变映射 [4] 。点云也可视为具有邻近点间潜在连边的图结构,因此采用图神经网络 (GNN) 处理点云数据成为自然选择。早期多数GNN方法 [5] 孤立处理各点,未显式利用局部邻域信息。虽然此类局部几何信息对高层任务有帮助,但这些方法期望网络直接从孤立输入点学习重要几何特征。动态边卷积网络 (Dynamic EdgeConv) [6] 证明局部几何属性对点云特征学习至关重要,其通过计算三维点与其邻域点的差值(可解释为三维方向向量)来编码局部结构。此外,该方法采用基于 $k$ 近邻的构图方式将点云转化为图,这是另一种可供模型使用的局部几何结构编码方式。该研究成功缩小了基于GNN的方法与其他最先进点云处理方法之间的性能差距。
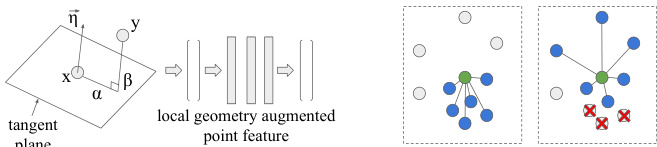
Fig. 1. We propose two components which work within the framework of graph neural networks for 3D point cloud processing. First, we propose to augment the point representations, not just by point features (e.g. coordinates) but also with local geometric information such as the in and out plane distances $\alpha,\beta$ (shown in left), w.r.t. the tangent plane of point $\mathbf{x}$ , to the nearby points, e.g. y. We further propose to non linearly project the resulting feature with a small neural network. Second, we propose to construct the local neighborhood graph in a geometrically aware way. While in the usual $k$ -NN based construction, the local graph can get biased towards a certain local neighborhood in the case of selective dense sampling, the proposed method aims to avoid that (shown in the two right blocks), by selecting the neighbors in a geometrically aware fashion. Best viewed in color.
图 1: 我们提出了两个在三维点云处理的图神经网络框架中工作的组件。首先,我们建议不仅通过点特征(如坐标)增强点表示,还加入局部几何信息,如相对于点 $\mathbf{x}$ 切平面的平面内外距离 $\alpha,\beta$ (如左图所示)到邻近点(如 y)。我们进一步提出使用小型神经网络对生成的特征进行非线性投影。其次,我们建议以几何感知的方式构建局部邻域图。在常规的 $k$ 近邻构建中,局部图在选择性密集采样情况下可能偏向特定邻域,而所提方法旨在通过几何感知方式选择邻居来避免这种情况(如右侧两个模块所示)。建议彩色查看。
Along the lines of Dynamic EdgeConv, we believe that presenting more geometric information encoded in a task relevant way is important for the success of GNNs for point cloud processing. The generic graph networks [5] were designed to work with general graphs, e.g. citation networks, social network graphs etc. In such graphs there is no notion of geometric relations between vertices. However, point cloud data is inherently geometric and one could expect the performance to increase when the two natural properties of the point cloud data, i.e. graph like structure, and geometric information, are co-exploited. We see Dynamic EdgeConv work as a step along, and propose to go further in this direction.
与 Dynamic EdgeConv 的思路一致,我们认为以任务相关的方式呈现更多编码的几何信息对于图神经网络 (GNN) 在点云处理中的成功至关重要。通用图网络 [5] 是为处理一般图结构设计的,例如引文网络、社交网络图等。这类图中不存在顶点间几何关系的概念。然而,点云数据本质上是几何的,当同时利用点云数据的两个固有特性(即类图结构和几何信息)时,性能有望提升。我们将 Dynamic EdgeConv 视为这一方向的阶段性成果,并提议在此方向上进一步探索。
We propose two novel, simple but extremely effective, components within the framework of general GNNs based on the intuitions above as shown in Figure 1. First, we propose to encode detailed local geometric information, inspired by traditional handcrafted 3D descriptors, about the points. Further, to convert the raw geometric information to a form which is easily exploited, we propose to use a multi layer perceptron network (MLP) to non linearly project the point features into another space. We then propose to present the projected representations as inputs to the graph network. This goes beyond the usual recommendation in previous works, where the possibility of adding more information about the point, e.g. color, depth, in addition to its 3D coordinates, has been often mentioned. We encode not only more information about the point, but also encode the information derived from the local neighborhood, around the point, as shown beneficial by previous works in handcrafted 3D descriptors. We also project such information non linearly to make it better exploitable by the GNN. While, in theory such information can be extracted by the neural network from 3D point coordinate inputs, we believe that presenting this information upfront allows the network to start from a better point, and even regularizes the learning.
基于上述直觉,我们在通用GNN框架中提出了两个新颖、简单但极其有效的组件,如图1所示。首先,受传统手工3D描述符启发,我们提出对点的局部几何信息进行精细编码。此外,为将原始几何信息转换为更易利用的形式,我们采用多层感知机网络(MLP)将点特征非线性映射到另一空间。随后将这些投影表征作为图网络的输入——这超越了以往工作中仅建议补充点信息(如颜色、深度等)的常规做法。我们不仅编码了更丰富的点信息,还编码了该点局部邻域派生的信息(正如手工3D描述符研究[20]所验证的),并通过非线性投影使GNN能更有效地利用这些信息。虽然理论上神经网络可从3D点坐标输入中提取此类信息,但我们认为预先提供这些信息能使网络从更优起点开始学习,并起到正则化作用。
Second, we propose a geometrically informed graph construction which goes beyond the usual $k$ -NN based construction. We constrain the sequential selection of points to be added to a local graph based on their angles and distances with already selected points, while considering the point of interest as the center of reference. This increases the coverage of the local connectivity and especially addresses cases where the points might be very densely sampled in one neighborhood, while relatively sparsely sampled in another.
其次,我们提出了一种基于几何信息的图构建方法,超越了常规的基于$k$-NN的构建方式。该方法以目标点作为参考中心,通过角度和距离约束来依次选择加入局部图的点。这种设计增强了局部连接性的覆盖范围,尤其适用于某些区域点采样极为密集而其他区域相对稀疏的情况。
We show empirically that both the contributions, while being relatively simple, are significant and help improve the performance of the baseline GNN. We report results on multiple publicly available challenging benchmarks of point clouds including both CAD models and real world 3D scans.
我们通过实证表明,这两个贡献虽然相对简单,但都具有重要意义,有助于提升基线 GNN (Graph Neural Network) 的性能。我们在多个公开的具有挑战性的点云基准测试上报告了结果,这些测试既包括 CAD 模型,也包括真实世界的 3D 扫描。
The results on the real world datasets help us make the point that the local geometry extraction methods work despite the noise in real world scans.
真实世界数据集的结果帮助我们证明,尽管现实扫描中存在噪声,局部几何提取方法仍然有效。
In summary, the contributions of this work are:
总之,本工作的贡献在于:
II. RELATED WORKS
II. 相关工作
Many tasks in 3D, such as classification and segmentation, can be solved by exploiting the local geometric structure of point clouds. In earlier efforts, handcrafted descriptors did this by encoding various properties of local regions in point clouds. The handcrafted descriptors, in general, fall into two categories. First are based on spatial distribution of the points, while the second directly utilize geometric properties of the points on surface.
3D中的许多任务,如分类和分割,可以通过利用点云的局部几何结构来解决。在早期研究中,手工设计的描述符通过编码点云中局部区域的各种属性来实现这一点。这些手工描述符通常分为两类:第一类基于点的空间分布,第二类则直接利用表面点的几何属性。
Most of the handcrafted descriptors are based on finding a local reference frame which provides robustness to various types of transformations of the point cloud. Spin Image [12] uses in-plane and out-plane distance of neighborhood points within the support region of the keypoint to discretize the space and construct the descriptor. Local Surface Patches [13], [14] utilizes shape index [15] and angle between normals to accumulate points forming the final descriptor.
大多数手工设计的描述符都基于寻找局部参考框架,这为点云的各种变换提供了鲁棒性。Spin Image [12] 使用关键点支撑区域内邻域点的面内和面外距离来离散化空间并构建描述符。Local Surface Patches [13][14] 则利用形状指数 [15] 和法线之间的角度来累积点,形成最终的描述符。
3D Binary Signatures [16] uses binary comparisons of geometrical properties in a local neighborhood. We refer the reader to Guo et al. [17] for a comprehensive survey of handcrafted 3D local descriptors.
3D Binary Signatures [16] 采用局部邻域内几何属性的二元比较方法。关于手工设计的3D局部描述符的全面综述,请参阅Guo等人的研究[17]。
Further, learning based methods have also been applied to obtain both local and global descriptors in 3D. Compact Geometric Features (CGF) [18] learns an embedding to a low dimensional space where the similar points are closer. DLAN [19] performs aggregation of local 3D features using deep neural network for the task of retrieval. Deep Point 3 D [20] learns disc rim i native local descriptors by using deep metric learning.
此外,基于学习的方法也被应用于获取3D中的局部和全局描述符。紧凑几何特征(CGF) [18]通过将数据嵌入到低维空间,使相似点更接近。DLAN [19]利用深度神经网络聚合局部3D特征以完成检索任务。Deep Point 3D [20]通过深度度量学习来学习具有判别性的局部描述符。
While 3D local descriptors are still preferred for tasks such as point cloud registration, 3D deep networks trained for generating a global descriptor have provided state-ofthe-art results on various classification, segmentation and retrieval benchmarks. The deep networks applied to these tasks are primarily based on volumetric representations (voxels, meshes, point clouds) and/or multi-view renderings of 3D shapes. We focus on techniques which directly process raw 3D point clouds as we work with them as well.
虽然3D局部描述符在点云配准等任务中仍占主导地位,但用于生成全局描述符的3D深度网络已在各类分类、分割和检索基准测试中取得了最先进的成果。应用于这些任务的深度网络主要基于体积表示(体素、网格、点云)和/或3D形状的多视角渲染。由于我们同样直接处理原始3D点云数据,因此重点关注这类直接处理技术。
PointNet [4] directly processes 3D point clouds by aggregating information using a symmetric function. PointNet $^{++}$ [21] applies hierarchical learning to PointNet to obtain geometrically more robust features. Kd-Net [22] constructs a network of kd-trees for parameter learning and sharing. PCNN [23], RS-CNN [24], LP-3DCNN [25], MinkowskiNet [26], FKAConv [27], PointASNL [28] propose modi- fications to convolution kernel or layers to produce features.
PointNet [4] 通过使用对称函数聚合信息直接处理3D点云。PointNet$^{++}$ [21] 在PointNet基础上应用分层学习以获得几何上更稳健的特征。Kd-Net [22] 构建kd树网络进行参数学习与共享。PCNN [23]、RS-CNN [24]、LP-3DCNN [25]、MinkowskiNet [26]、FKAConv [27]、PointASNL [28] 提出了针对卷积核或网络层的改进方案以生成特征。
Recently, graph based neural networks have shown good performance on such unstructured data [29]–[31]. Dynamic Edge Convolutional Neural Network (DGCNN) [6] showed that by representing the local neighborhood of a point as a graph, it can achieve better performance than the previous techniques. Moreover, many previous works such as PointNet, PointNet++ become a special case with various Edge Convolution functions. LDGCNN [32] extends DGCNN by hierarchically linking features from the dynamic graphs in DGCNN. Authors in [33], [34] propose modifications to kernels to capture geoemtric relationships between points.
最近,基于图的神经网络在此类非结构化数据上表现出良好的性能[29]–[31]。动态边缘卷积神经网络(DGCNN)[6]表明,通过将点的局部邻域表示为图,其性能优于先前技术。此外,PointNet、PointNet++等许多先前工作通过不同边缘卷积函数成为特例。LDGCNN[32]通过分层链接DGCNN中动态图的特征扩展了该架构。[33][34]的作者提出修改核函数以捕捉点之间的几何关系。
Our proposals are mainly within the purview of GNNs, however we extensively compare with most of the existing 3D point cloud based methods and show better results.
我们的方案主要基于图神经网络 (GNN) 范畴,但与现有大多数基于 3D 点云的方法进行了广泛对比,并展示了更优的结果。
III. APPROACH
III. 方法
We are interested in processing a set $\mathbf{X}$ , i.e. a point cloud, of 3D points. We follow the general graph neural network (GNN) based processing, where we work with a directed graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ with the points being the vertices $\nu$ and the edges being potential connections between them. The vertices in $\nu$ are represented by a $D$ dimensional feature vector, which is often just the 3D coordinate of the points, and the set of edges is constructed usually with a $k$ -NN based graph construction algorithm. We now describe our two contributions pertaining to (i) the representation of the points using local geometric information and (ii) constructing the graph edges $\mathcal{E}$ with a geometrically constrained algorithm. Figure 2 gives an overall block diagram of our full system.
我们致力于处理一组3D点$\mathbf{X}$,即点云。采用基于图神经网络(GNN)的通用处理方法,构建有向图$\mathcal{G}=(\mathcal{V},\mathcal{E})$,其中顶点$\nu$对应点云中的点,边表示点之间的潜在连接。顶点$\nu$通过$D$维特征向量表示(通常仅为点的3D坐标),边集则通常采用基于$k$近邻($k$-NN)的图构建算法生成。本文的两个核心贡献在于:(i) 利用局部几何信息表示点云;(ii) 通过几何约束算法构建图边集$\mathcal{E}$。图2展示了完整系统的总体框图。
A. Local Geometric Representation of Points
A. 点的局部几何表示
Majority of the GNN based previous works use a basic representations of points, i.e. their 3D coordinates, and feed that to the GNN to extract more complex interactions between neighboring points. Since GNNs, e.g. [5], were designed for general graphs which may not have any geometric properties, e.g. social network graphs, they do not have any explicit mechanism to encode geometry. More recent works on point cloud processing have started exploiting the geometric nature of 3D data more explicitly. As a specific case, EdgeConv [6] uses an edge function of the form
多数基于图神经网络 (GNN) 的先前工作使用点的基本表示(即其3D坐标),并将其输入GNN以提取相邻点之间更复杂的交互。由于GNN(例如[5])是为可能没有任何几何属性(例如社交网络图)的通用图设计的,它们没有任何显式机制来编码几何。最近关于点云处理的工作开始更明确地利用3D数据的几何性质。具体来说,EdgeConv [6] 使用以下形式的边缘函数
$h_{\Theta}(\mathbf{x}{i},\mathbf{x}{j})=\bar{h}{\Theta}(\mathbf{x}{i},\mathbf{x}{j}-\bar{\mathbf{x}_{i}})$ .
$h_{\Theta}(\mathbf{x}{i},\mathbf{x}{j})=\bar{h}{\Theta}(\mathbf{x}{i},\mathbf{x}{j}-\bar{\mathbf{x}_{i}})$ .
where $\mathbf{x}{i}$ is the point under consideration, and $\mathbf{x}{j}$ is one of its neighbors. $h_{\Theta}$ is a nonlinear function and $\Theta$ is a set of learnable parameters. This function thus specifically uses a global description of the point, i.e. the point coordinates themselves, and a local description, which is the direction vector from the point to a nearby point. Providing such explicit local geometric description as input to the network layers helps EdgeConv outperform the baseline GNNs.
其中 $\mathbf{x}{i}$ 是当前考虑的点,$\mathbf{x}{j}$ 是其邻近点之一。$h_{\Theta}$ 是一个非线性函数,$\Theta$ 是可学习参数集。该函数专门使用了点的全局描述(即点坐标本身)和局部描述(从该点到邻近点的方向向量)。将这种显式的局部几何描述作为网络层的输入,使得 EdgeConv 能够超越基线 GNNs。
We go further in this direction and propose to use detailed geometric description of the local neighborhood of the point. Significant ingenuity was spent on the design of handcrafted 3D features (see [17] for a comparison), before deep neural networks became competitive for 3D point cloud processing. We take inspiration from such works in deriving the geometric descriptions of the points.
我们沿着这一方向更进一步,提出利用点云局部邻域的精细几何描述。在深度神经网络尚未胜任3D点云处理任务前,研究者们曾耗费大量精力设计手工3D特征(对比研究见[17])。我们从这些工作中汲取灵感,用于推导点的几何描述。
We include the following components in the representation of each point. As used in previous works, the first part is plain 3D coordinates of the point $(x,y,z)$ , followed by the normal vector $\vec{\eta}=\left(\eta_{x},\eta_{y},\eta_{z}\right)$ of the point. Then we take inspiration from the Spin Image descriptor [12] and add the in-plane and out-plane distances $\alpha,\beta$ w.r.t. the point. Finally, inspired by the Local Surface Patch Descriptor [13], [14], we include the shape index $(\gamma)$ as well.
每个点的表示包含以下组成部分。如先前工作所述,第一部分是点的三维坐标 $(x,y,z)$,接着是该点的法向量 $\vec{\eta}=\left(\eta_{x},\eta_{y},\eta_{z}\right)$。随后我们借鉴Spin Image描述符[12],添加了相对于该点的面内和面外距离 $\alpha,\beta$。最后,受局部曲面块描述符[13][14]启发,我们还引入了形状指数 $(\gamma)$。
Hence, compared to a simple 3D coordinate based description of the points, we represent them with a 9D descriptor $\mathbf{p}=(x,y,z,\eta_{x},\eta_{y},\eta_{z},\alpha,\beta,\gamma)$ containing more local contextual geometric information. We then further pass this 9D descriptor through a small neural network $\phi(\cdot)$ to non linearly project it into another space which is more adapted to be used with the GNN. Finally, we pass the non linearly projected point representation $\phi(\mathbf{p})$ to the graph neural network.
因此,相较于基于简单3D坐标的点描述方式,我们采用一个包含更多局部上下文几何信息的9D描述符 $\mathbf{p}=(x,y,z,\eta_{x},\eta_{y},\eta_{z},\alpha,\beta,\gamma)$ 来表示这些点。随后,我们将这个9D描述符输入一个小型神经网络 $\phi(\cdot)$,通过非线性映射将其转换到更适合与图神经网络 (GNN) 结合使用的空间。最终,我们将非线性映射后的点表示 $\phi(\mathbf{p})$ 传递给图神经网络。
While one can argue that such augmentation may be redundant as the GNN should be able to extract it out from 3D coordinates only, we postulate that providing these, successful handcrafted descriptor inspired and non linearly projected features, makes the job of the GNN easier. Another argument could be raised that these descriptors might be very task specific and hence might not be needed for a task of interest. In that case, we would argue that it should be possible for GNN to essentially ignore them by learning zero weights for weights/edges corresponding to these input units in the neural network. While this is a seemingly simple augmentation, we show empirically in Section IV that, in fact, adding such explicit geometric information does help the tasks of classification, part segmentation and semantic segmentation on challenging benchmarks, both based on clean CAD models of objects, as well as from real world noisy scans of indoor and outdoor spaces.
虽然有人可能认为这种增强可能是多余的,因为 GNN 应该能够仅从 3D 坐标中提取出这些信息,但我们假设提供这些受成功手工描述符启发并经过非线性投影的特征,可以使 GNN 的工作更容易。另一个可能的论点是这些描述符可能非常特定于任务,因此对于感兴趣的任务可能不需要。在这种情况下,我们认为 GNN 应该能够通过学习神经网络中与这些输入单元对应的权重/边的零权重来本质上忽略它们。虽然这看似是一个简单的增强,但我们在第 IV 节中通过实验证明,事实上,添加这种显式的几何信息确实有助于在具有挑战性的基准测试中进行分类、部件分割和语义分割任务,这些基准测试既基于干净的物体 CAD 模型,也来自室内外空间的实际噪声扫描。
B. Geometrically Constrained Neighborhood Graph Construction
B. 几何约束邻域图构建
Once the feature description is available, the next step is to define the directed edges between the points to fully construct the graph. We now detail our second contribution pertaining to the construction of the graph.
一旦特征描述可用,下一步就是定义点之间的有向边以完整构建图。我们现在详细说明与图构建相关的第二个贡献。
Previous methods construct the graphs using a $k$ -NN scheme. Each point is considered, and directed edges are added from the point to its $k$ nearest neighbors. The graph thus constructed is given as input to the GNN which performs the final task.
先前的方法采用$k$-NN(近邻)方案构建图结构:为每个节点创建指向其$k$个最近邻的有向边,生成的图将作为GNN的输入以执行最终任务。
A $k$ -NN based graph construction scheme, while being intuitive and easy to implement, has an inherent problem. It is not robust to sampling frequency difference which can happen often in practice. Certain object may be densely sampled at some location in the scene, but the same object when placed at another location in the scene might only be sparsely sampled. Such scenarios can happen, for instance, in LiDAR based scanning, where the spatial sampling frequency is higher when the object is nearer to the sensor, but is lower when the object is farther. In such cases, $k$ -NN may not cover the object sufficiently when the sampling density is higher, as all the $k$ nearest neighbors might be very close together, as shown in Figure 1 (center), and fall on the same subregion of the object. Hence, we propose a locality adaptive graph construction algorithm which promotes coverage in the local graph.
基于 $k$ -NN 的图构建方案虽然直观且易于实现,但存在一个固有缺陷:它对采样频率差异缺乏鲁棒性,而这种情况在实践中经常发生。某些物体在场景中某一位置可能被密集采样,但同一物体置于场景另一位置时可能仅被稀疏采样。例如,在基于 LiDAR 的扫描中,物体距离传感器较近时空间采样频率较高,较远时则较低。此时若采样密度较高, $k$ -NN 可能无法充分覆盖物体——如图 1 (center) 所示,所有 $k$ 个最近邻可能过于聚集,落在物体的同一子区域。为此,我们提出一种局部自适应的图构建算法,以提升局部图的覆盖能力。
The design of the graph construction is inspired by logpolar histograms which have been popular for many engineering applications. The main element is illustrated in Figure 3 in the case of 2D points. The construction iterates over each point one by one, and considers the sorted nearest neighbors of each point. However, instead of selecting the $k$ -NN points, it greedily selects the neighbors as follows. At point $\mathbf{x}$ , as soon as it selects a point y, it removes all constructed in a geometrically constrained way. We stress here that while we give results with one specific choice of GNN in this paper, our graph can be used with any available GNN working on the input graph $\mathcal{G}$ .
图构建的设计灵感来源于对数极坐标直方图(logpolar histograms),这种结构在众多工程应用中广受欢迎。如图3所示(以二维点为例),该构建过程会逐个遍历每个点,并考虑每个点的排序最近邻。但与直接选择k近邻($k$-NN)点不同,它采用如下贪婪策略选择邻点:在点$\mathbf{x}$处,每当选中一个点y,就会以几何约束方式移除所有已构建的连接。需要强调的是,虽然本文展示的成果采用特定图神经网络(GNN)实现,但所构建的图结构$\mathcal{G}$可兼容任何能处理输入图的现有GNN模型。
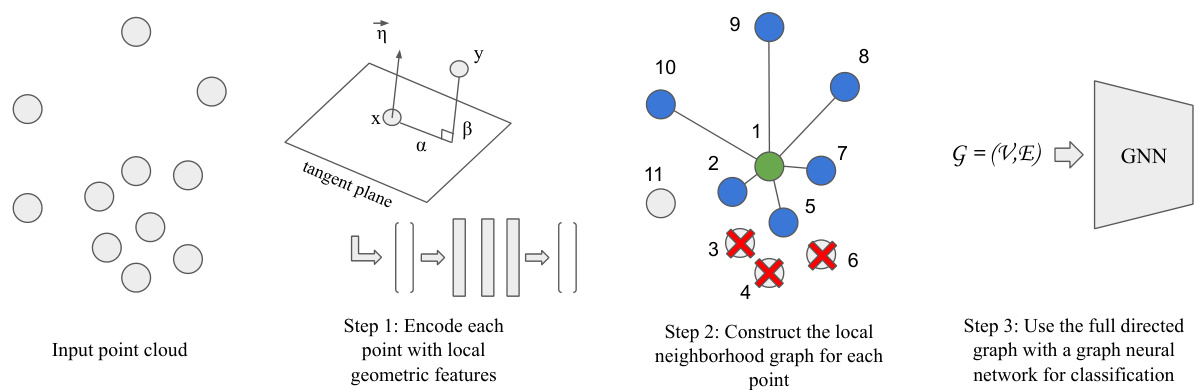
Fig. 2. Illustration of of the proposed method. The input point cloud is processed point by point to generate an eventual graph, with vertices represented as real vectors and having directed edges denoting local neighborhoods. The representation includes local geometric properties of the points (which is relative to other points in their neighborhood), along with their coordinates. The graph formulation is geometrically aware and counters oversampling in some regions of the space. The finally constructed graph can then be used with a graph neural network for supervised learning, e.g. for classification and part segmentation. Best viewed in color.
图 2: 所提方法示意图。输入点云被逐点处理以生成最终图结构,其中顶点表示为实值向量,有向边表示局部邻域关系。该表征包含点的局部几何属性(相对于其邻域内其他点)及其坐标信息。这种图构建方式具有几何感知能力,可缓解空间某些区域的过采样问题。最终构建的图可用于图神经网络的监督学习任务,例如分类和部件分割。建议彩色查看。

IV. EXPERIMENTAL RESULTS
IV. 实验结果
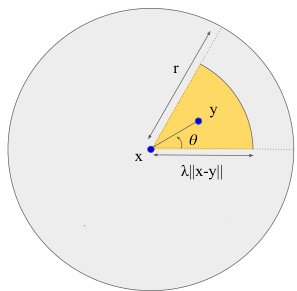
Fig. 3. The local neighborhood graph construction constraints in 2D: Once a point $y$ is selected, for a point $x$ , points from the yellow region, i.e. within an angle $\theta$ and a distance $\bar{\lambda||}x-y|$ are discarded. This encourages coverage, and tackles densely sampled parts, in the local neighborhood graph. Best viewed in color.
图 3: 二维局部邻域图构建约束:当选定点 $y$ 后,对于点 $x$ ,黄色区域内的点(即角度 $\theta$ 范围内且距离小于 $\bar{\lambda||}x-y|$ 的点)将被剔除。该方法提升了局部邻域图的覆盖性,并有效处理密集采样区域。建议彩色查看。
points in the region within an angle $\theta$ from the line $\mathbf{y}-\mathbf{x}$ with origin at $\mathbf{x}$ , and with distance less than $\lambda|\mathbf x-\mathbf y|$ , with both $\theta,\lambda$ being tunable hyper parameters, shown as the region marked in yellow in Figure 3. The simple intuition being that once a point from a local neighborhood has been sampled, we look for points which are sufficiently away from that local neighborhood. This ensures coverage in the local graph construction and improves robustness to sensor sampling frequency artefacts.
以点 $\mathbf{x}$ 为原点,在 $\mathbf{y}-\mathbf{x}$ 方向线 $\theta$ 角度范围内,且距离小于 $\lambda|\mathbf x-\mathbf y|$ 的区域内的点(其中 $\theta,\lambda$ 为可调超参数),如图3黄色标记区域所示。其直观逻辑是:一旦从局部邻域采样了一个点,我们会寻找与该邻域保持足够距离的其他点。这确保了局部图构建的覆盖性,并提升对传感器采样频率伪影的鲁棒性。
To illustrate the construction with a small toy example, we refer to Figure 2 (step 2). In the usual $k$ -NN based graph construction, w.r.t. point 1, the points which would have been selected would be $2,3,4,5,6,7$ (for $k=6$ ), which would concentrate the local neighborhood graph only on one region of the space. In contrast, with the proposed method, with appropriate $\theta,\gamma$ , the selection of points $3,4,6$ can be avoided due to the presence of 2, 5, and the final six selected points would be $2,5,7,8,9,10$ which are well distributed in the space around the main point. Hence the problem of oversampling in some regions by the sensor can be avoided.
为了通过一个小型示例说明构建过程,我们参考图 2 (步骤 2)。在传统的基于 $k$ -NN 的图构建方法中,对于点 1,通常会选择点 $2,3,4,5,6,7$ (当 $k=6$ 时),这将导致局部邻域图仅集中在空间的一个区域。相比之下,采用所提出的方法时,通过合适的 $\theta,\gamma$ 参数,可以避免选择点 $3,4,6$,因为存在点 2 和 5,最终选中的六个点将是 $2,5,7,8,9,10$,这些点在主点周围的空间中分布良好。因此,可以避免传感器在某些区域过采样的问题。
C. Use with GNN
C. 与 GNN 结合使用
Given the above point descriptions, as well as graph edge constructions, we have a fully specified graph $\mathcal{G}=$ $(\nu,\mathcal{E})$ derived from the point cloud data. This graph is general enough to be used with any GNN algorithm, while being specific to 3D point clouds as the vertex descriptions contain local geometric information, and the edges have been
根据上述点描述及图边构建方式,我们从点云数据中导出了一个完全指定的图$\mathcal{G}=$$(\nu,\mathcal{E})$。该图具有足够通用性,可与任何图神经网络(GNN)算法配合使用,同时专门针对3D点云——其顶点描述包含局部几何信息,且边结构也...
We now give the results of the proposed methods on challenging benchmarks.
我们现在给出所提方法在具有挑战性的基准测试上的结果。
We denote the proposed methods as (i) ours (representation), when we incorporate the proposed local geometric representation, and (ii) ours (representation $^+$ graph) when we incorporate the proposed geometrically constrained graph construction as well.
我们将提出的方法分别表示为:(i) ours (representation),即采用提出的局部几何表征时;(ii) ours (representation $^+$ graph),即同时采用提出的几何约束图构建方法时。
A. Datasets and Experimental Setup
A. 数据集与实验设置
We evaluate the proposed method on the following datasets ModelNet40 [7], ShapeNet [8], ScanNet [9], Stanford LargeScale 3D Indoor Spaces (S3DIS) scans [10], and Paris-Lille3D (PL3D) [11]. We follow standard settings for training and evaluation on respective datasets. We use Dynamic Edge Convolutional network (DGCNN) [6] as the baseline network. Further, the input to the MLP is the 9D vector, it contains two FC layers with 18 and 9 units respectively.
我们在以下数据集上评估所提出的方法:ModelNet40 [7]、ShapeNet [8]、ScanNet [9]、斯坦福大规模3D室内空间(S3DIS)扫描 [10] 和巴黎-里尔3D(PL3D) [11]。我们遵循各数据集的训练与评估标准设置,采用动态边缘卷积网络(DGCNN) [6] 作为基线网络。此外,多层感知机(MLP)的输入为9维向量,包含两个全连接层(FC),分别具有18和9个单元。
B. Parametric Study
B. 参数研究
Table I gives the performances of the methods with different number of nearest neighbors. We see that for the baseline method, DGCNN with $k$ -NN based graph construction, the performance initially increases with an increase in $k$ but then the drops a little, e.g. mean class accuracy goes from 88.0 to 90.2 for $k=5,20$ , b
