Dynamic Multi-Task Learning for Face Recognition with Facial Expression

动态多任务学习在人脸识别与表情分析中的应用

Abstract

摘要

Benefiting from the joint learning of the multiple tasks in the deep multi-task networks, many applications have shown the promising performance comparing to single-task learning. However, the performance of multi-task learning framework is highly dependant on the relative weights of the tasks. How to assign the weight of each task is a critical issue in the multi-task learning. Instead of tuning the weights manually which is exhausted and time-consuming, in this paper we propose an approach which can dynamically adapt the weights of the tasks according to the difficulty for training the task. Specifically, the proposed method does not introduce the hyper parameters and the simple structure allows the other multi-task deep learning networks can easily realize or reproduce this method. We demonstrate our approach for face recognition with facial expression and facial expression recognition from a single input image based on a deep multi-task learning Conventional Neural Networks (CNNs). Both the theoretical analysis and the experimental results demonstrate the effectiveness of the proposed dynamic multi-task learning method. This multi-task learning with dynamic weights also boosts of the performance on the different tasks comparing to the state-of-art methods with single-task learning. 1

得益于深度多任务网络中多任务的联合学习，许多应用相较于单任务学习展现出了优异的性能。然而，多任务学习框架的性能高度依赖于各任务的相对权重。如何分配每个任务的权重是多任务学习中的关键问题。本文摒弃了耗时费力的人工权重调参方式，提出了一种根据任务训练难度动态调整权重的算法。具体而言，该方法无需引入超参数，其简洁结构使得其他多任务深度学习网络能轻松实现或复现。我们基于深度多任务学习卷积神经网络（Conventional Neural Networks, CNNs），通过单张输入图像同时进行人脸识别与面部表情识别的实验验证了该方法的有效性。理论分析与实验结果均表明，所提出的动态多任务学习方法具有显著优势。与当前最先进的单任务学习方法相比，这种动态权重多任务学习机制在不同任务上均实现了性能提升。[1]

1. Introduction

1. 引言

Multi-task learning has been used successfully across many areas of machine learning [26], from natural language processing and speech recognition [6, 7] to computer vision [10]. By joint learning in multiple tasks in the related domains with different information, especially from information-rich tasks to information-poor ones, the multi-task learning can capture a representation of features being difficult learned by one task but can easily learned by another task [23]. Thus the multi-task learning can be conducted not only for improving the performance of the systems which aims to predict multiple objectives but also can utilise for improving a specific task by leveraging the related domain-specific information contained in the auxiliary tasks. In this work, we explore the multi-learning for face recognition with facial expression. Thanks to the progress of the representing learning with the deep CNNs, face recognition has made remarkable progress in the recent decade [31, 24, 27, 19]. These works have achieved or beyond the human-level performance on the benchmarks LFW[13], YTF[34]. The challenges of face recognition such as the variation of the pose, the illumination and the occlusion have been well investigated in many researches, nevertheless face recognition for the face with the non-rigid deformation such as the ones introduced by the facial expression has not been sufficiently studied especially in the 2D face recognition domain. Some 3D based methods have been proposed to deal with this issue such as [41, 15, 3], in which [41] presents the method by using the 3D facial model to normalise the facial expression and then maps the normalised face to the 2D image to employ face recognition. In order to leverage the promising progress in the numerous 2D face recognition and facial expression recognition researches particularly based on the deep neural networks, we propose to combine the face recognition task and the facial expression recognition task in the unified multi-task framework aiming to jointly learn the sharing features and task-specific features to boost the performance of each task. Figure 1 shows the multi-task framework proposed in this work.

多任务学习已在机器学习多个领域成功应用[26]，从自然语言处理、语音识别[6,7]到计算机视觉[10]。通过在相关领域联合学习携带不同信息的多个任务（特别是从信息丰富的任务迁移到信息匮乏的任务），多任务学习能够捕捉那些单任务难以学习但其他任务易于获取的特征表示[23]。因此，多任务学习不仅能提升多目标预测系统的性能，还能通过辅助任务中的领域特定信息来增强特定任务的表现。本文探索了结合面部表情的人脸识别多任务学习。得益于深度卷积神经网络(CNN)在表征学习方面的进展，近十年来人脸识别取得了显著突破[31,24,27,19]，这些工作已在LFW[13]、YTF[34]等基准测试中达到或超越人类水平。虽然姿态、光照和遮挡等传统挑战已被广泛研究，但针对表情引起的非刚性变形的人脸识别（尤其是2D领域）仍未得到充分探索。部分基于3D的方法如[41,15,3]尝试解决该问题，其中[41]提出通过3D面部模型归一化表情后再映射到2D图像进行识别。为充分利用2D人脸识别与表情识别（特别是基于深度神经网络）的研究成果，我们提出在统一的多任务框架中结合这两个任务，通过联合学习共享特征和任务专属特征来提升各自性能。图1展示了本研究的框架。

How to set the weights of tasks is a crucial issue in the multi-task learning. The weights determine the importance of the different tasks in the holistic networks. Many works simply set the equal values for all tasks or experimentally set the weights of the tasks. In [4], the authors assign equal weights to the ranking task and the binary classification task for the person re-identification. However the multi-task learning is an optimization problem for multiple objectives.

在多任务学习中，如何设置任务权重是一个关键问题。权重决定了不同任务在整个网络中的重要性。许多工作简单地为所有任务设置相同值，或通过实验性方式设定任务权重。在[4]中，作者为行人重识别任务中的排序任务和二元分类任务分配了相等权重。然而多任务学习本质上是一个多目标优化问题。

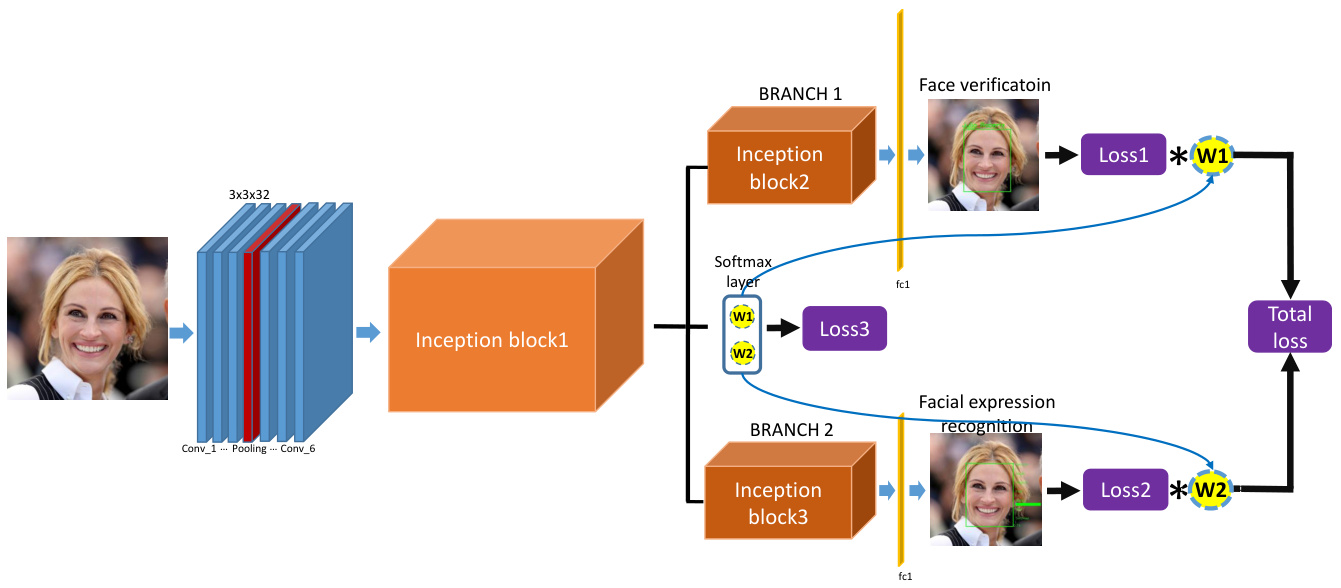
Figure 1: The proposed multi-task framework with dynamic weights of tasks to simultaneously perform face recognition and facial expression recognition. The dynamic weights of tasks can adapt automatically according to the importance of tasks.

图 1: 提出的多任务动态权重框架，可同时执行人脸识别和面部表情识别。任务动态权重能根据任务重要性自动调整。

The main task and the side tasks with different objective have different importance in the overall loss meanwhile the difficulty of the training of each task is also different. Thus it is arbitrary to assign equal weights for tasks for multi-task learning. We also verified this point in our work by manually setting the weights of tasks from 0 to 1 with the interval of 0.1. As shown in Figure 2, either for the facial expression recognition task or for the face recognition task, the best performance are obtained with the different weights of tasks rather than the equal weights of each task. Most of the multi-task learning methods search the optimal weights of the tasks by the experimental methods, for instance Hyperface [25] manually set the weights of the tasks such as the face detection, landmarks localization, pose estimation and gender recognition according to their importance in the overall loss, and [32] obtain the optimal weights by a greedy search for pedestrian detection tasks with the different attributes. Besides the cost of time and being exhausting, these methods setting the weights as the fix values to optimize the tasks ignore the variation of the the importance or the difficulty of the tasks during the training processing. Rather than the methods with fix weights which can be so called static weights methods, the methods [5, 16, 38] update the weights or part of the weights of the tasks during the training of the networks. [38] set the weight of the main task as 1 while the auxiliary tasks are weighted by the dynamic weights $\lambda_{t}$ which are updated by an analytical solution. [16] introduces a uncertainty coefficient $\theta$ to revise the softmax loss function of each task. Unlike these methods which need to introduce the additional hyper parameters to update the weights of tasks, we propose to use a softmax layer adding to the end of the hidden sharing layers of the multi-task networks to generate the dynamic weights of the tasks (see Figure 1). Each unit of this softmax layer is corresponding to a weight of a task and no more hyper parameter is introduced for updating the tasks weights. Rather than [36] updating simultaneously the dynamic weights of tasks and the filters weights of the networks by the unify total loss of the networks, we propose a new loss function to update the dynamic weights which enable the networks to focus on the training of the hard task by automatically assigning a larger weight. On the contrary, [36] always updates the smaller weight for the hard task and the larger weight for the easy task which results the hard task is far from being fully trained and the networks stuck in the worthless training of the over trained easy task. This is due to use the total loss of the networks to simultaneously update the weights of tasks, in which the dynamic weights of the tasks are also in the function of the weights of networks, i.e. $\mathcal{L}{t o t a l}(\Theta)=$ $w_{1}(\Theta_{0})\mathcal{L}{1}(\Theta_{1})+w_{2}(\Theta_{0})\mathcal{L}{2}(\Theta_{2})$ s.t. $w_{1}+w_{2}=1$ and ${\Theta_{0},\Theta_{1},\Theta_{2}}=\Theta$ are the weights of the networks. The optimization of $\Theta$ by the total loss $\mathcal{L}{t o t a l}$ aims to decrease the total loss as much as possible, thus when the hard task has a large loss the fastest way to decrease the total loss is to shrinkage its weight $w_{i}$ so that the weighted loss of the hard task can be cut down rapidly. This is why the hard task always has a small task weight while the easy task has a large weight.

在多任务学习中，主任务和不同目标侧任务在整体损失中的重要性不同，同时各任务的训练难度也存在差异。因此为任务分配相等权重具有随意性。我们通过手动将任务权重以0.1为间隔从0调整到1进行验证，如图2所示，无论是面部表情识别任务还是人脸识别任务，最佳性能都出现在不同任务权重的配置下，而非均等权重状态。大多数多任务学习方法通过实验手段搜索最优任务权重，例如Hyperface [25] 根据人脸检测、关键点定位、姿态估计和性别识别在总体损失中的重要性手动设置权重，[32]则通过贪婪搜索为不同属性的行人检测任务获取最优权重。这些将权重设为固定值的方法不仅耗时费力，还忽略了训练过程中任务重要性或难度的动态变化。

区别于静态权重方法，[5,16,38]等研究在网络训练期间动态更新任务权重。[38]将主任务权重固定为1，辅助任务权重通过解析解动态更新参数$\lambda_{t}$进行调整。[16]引入不确定性系数$\theta$来修正各任务的softmax损失函数。不同于这些需要引入额外超参数的方法，我们提出在多任务网络共享隐藏层末端添加softmax层来生成动态任务权重（见图1）。该softmax层的每个单元对应一个任务权重，且无需引入额外超参数进行更新。

与[36]使用网络总损失同步更新任务动态权重和网络滤波器权重不同，我们提出新的损失函数来更新动态权重，使网络能通过自动分配更大权重聚焦困难任务的训练。而[36]总是为困难任务分配较小权重、为简单任务分配较大权重，导致困难任务无法充分训练，网络陷入对过度训练简单任务的无价值学习中。这是因为其使用网络总损失$\mathcal{L}{total}(\Theta)=w_{1}(\Theta_{0})\mathcal{L}{1}(\Theta_{1})+w_{2}(\Theta_{0})\mathcal{L}{2}(\Theta_{2})$（约束条件$w_{1}+w_{2}=1$且${\Theta_{0},\Theta_{1},\Theta_{2}}=\Theta$为网络权重）同步优化时，当困难任务损失较大时，降低总损失的最快途径是缩减其权重$w_{i}$，这导致困难任务始终获得较小权重而简单任务获得较大权重。

In a summary, our main contributions of this paper are.

综上所述，本文的主要贡献包括。

We propose a dynamic multi-task learning method which can automatically update the weight of task according to the importance of task during the training. • Both the theoretical analysis and the experimental results demonstrate the proposed dynamic multi-task learning enable to focus on the training of the hard task to achieve better efficiency and performance.

我们提出了一种动态多任务学习方法，该方法能在训练过程中根据任务重要性自动更新任务权重。理论分析和实验结果均表明，所提出的动态多任务学习能够聚焦困难任务的训练，从而获得更高的效率和性能。

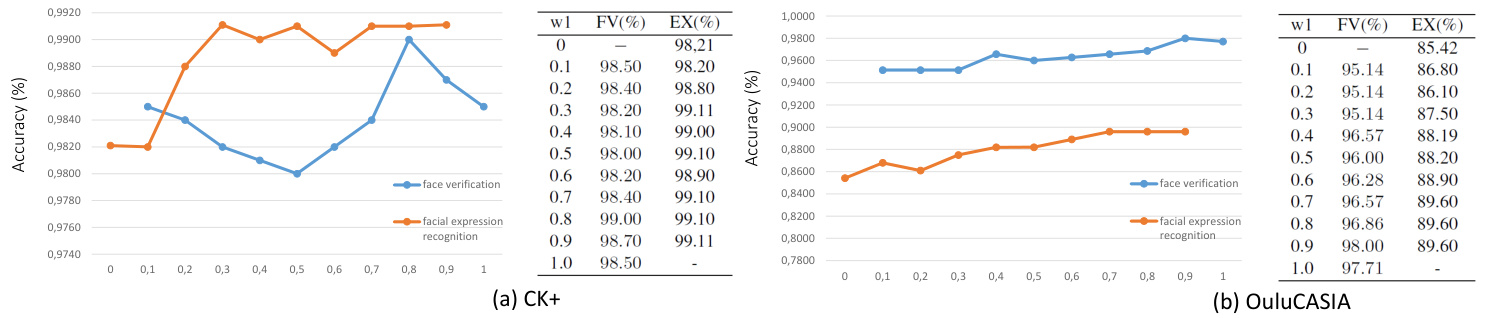
Figure 2: Performances of the task of face verification for facial expression images (FV / blue) with the manually setting weight $w1$ and the task of facial expression recognition (EX / red) on the different datasets $\mathrm{CK}+$ and OuluCASIA.

图 2: 在不同数据集 CK+ 和 OuluCASIA 上，手动设置权重 $w1$ 的人脸验证任务 (FV / 蓝色) 与面部表情识别任务 (EX / 红色) 的性能对比。

The remainder of this paper is organized as follows: Section II briefly reviews the related works; Section III de- scribes the architecture of the dynamic multi-task network. Section IV presents the approach of multi-task learning with dynamic weights following by Section V where the experimental results are analyzed. Finally, in Section VI, we draw the conclusions and present the future works.

本文的剩余部分结构如下：第二节简要回顾相关工作；第三节描述动态多任务网络的架构；第四节介绍动态权重的多任务学习方法，随后第五节分析实验结果。最后，第六节总结结论并提出未来工作方向。

2. Related works

2. 相关工作

Multi-task learning not only helps to learn more than one task in a single network but also can improve upon your main task with an auxiliary task [26]. In this work, we focus on the multi-task learning in the context of the deep CNNs. According to the means of updating the weights of tasks, the multi-task learning can be divided into two categories: the static method and dynamic method. In the static methods, the weights of tasks are set manually before the training of the networks and they are fixed during the whole training of the networks [25, 10, 4, 35, 32]; while the dynamic methods initialize the weights of the tasks at the beginning of the training and update the weights during the training processing [5, 16, 38, 36]. There are two ways for setting the weights in the static methods. The first way is to simply set the equal weights of task such as Fast R-CNN [10] and [4, 35]. In Fast R-CNN, the author uses a multi-task loss to jointly train the classification and bounding-box regression for object detection. The classification task is set as the main task and the bounding-box regression is set as the side task weighted by $\lambda$ . In the experiments the $\lambda$ is set to 1. The second way to set the weights is manually searching the optimal weights by the experimental methods. Hyperface [25] proposed a multi-task learning algorithm for face detection, landmarks localization, pose estimation and gender recognition using deep CNNs. The tasks have been set the different weights according to the importance of the task. [4] integrated the classification task and the ranking task in a multi-task networks for person reidentification problem. Each task has been set with a equal weight to jointly optimizing the two tasks simultaneously. Tian et al. [32] fix the weight for the main task to 1, and obtain the weights of all side tasks via a greedy search within 0 and 1. In [5] an additional loss in function of the gradient of the weighted losses of tasks is proposed to update the weights meanwhile an hyper parameter is introduced for balancing the training of different tasks. [16] introduces a uncertainty coefficient $\theta$ to combine the multiple loss functions. The $\theta$ can be fixed manually or learned based on the total loss. Zhang et al. [38] propose a multi-task networks for face landmarks detection and the recognition of the facial attributes. The face landmarks detection is set as the main task with the task weight 1 and the tasks for recognition of the different facial attributes are set as auxiliary tasks with dynamic weights $\lambda_{t}$ . An hyper parameter $\rho$ as a scale factor is introduced to calculate the weight $\lambda_{t}$ . Yin et al. [36] proposed a multi-task model for face pose-invariant recognition with an automatic learning of the weights for each task. The main task of is set to 1 and the auxiliary tasks are sharing the dynamic tasks generated by the softmax layer. However, the update of the weights of tasks by the total loss of the networks runs counter to the objective of the multi-task learning. Thanks to the progress of the representation learning based on the deep neural networks, the methods based on the deep CNNs such as DeepFace [31] , DeepIDs [30], Facenet [27], VGGFace [29],

多任务学习不仅有助于在单一网络中学习多个任务，还能通过辅助任务提升主任务性能 [26]。本文聚焦于深度卷积神经网络 (CNN) 背景下的多任务学习。根据任务权重更新方式，多任务学习可分为静态方法和动态方法两类：静态方法在网络训练前手动设置任务权重，并在整个训练过程中固定不变 [25, 10, 4, 35, 32]；而动态方法在训练初期初始化任务权重，并在训练过程中动态更新 [5, 16, 38, 36]。

静态方法设置权重有两种途径。第一种是简单设置任务等权重，如 Fast R-CNN [10] 和 [4, 35]。Fast R-CNN 采用多任务损失联合训练目标检测的分类与边界框回归任务，将分类设为主任务（权重1），边界框回归设为辅助任务（权重$\lambda$），实验中设定$\lambda=1$。第二种是通过实验方法手动搜索最优权重：Hyperface [25] 提出基于深度CNN的人脸检测、关键点定位、姿态估计和性别识别多任务算法，根据任务重要性分配不同权重；[4] 将分类任务与排序任务集成于行人重识别的多任务网络，采用等权重联合优化；Tian等 [32] 固定主任务权重为1，通过0到1区间贪婪搜索获取所有辅助任务权重。

动态方法方面：[5] 提出根据任务加权损失梯度函数计算附加损失来更新权重，同时引入超参数平衡不同任务训练；[16] 采用不确定性系数$\theta$组合多损失函数，$\theta$可手动固定或基于总损失学习；Zhang等 [38] 构建人脸关键点检测（主任务，权重1）与属性识别（辅助任务，动态权重$\lambda_{t}$）的多任务网络，引入缩放因子$\rho$计算$\lambda_{t}$；Yin等 [36] 提出面向姿态不变人脸识别的多任务模型，通过softmax层自动学习任务权重（主任务固定为1，辅助任务共享动态权重），但基于网络总损失更新权重的方式与多任务学习目标存在矛盾。

得益于深度神经网络表征学习的进展，基于深度CNN的方法如DeepFace [31]、DeepIDs [30]、Facenet [27]、VGGFace [29]等...

SphereFace [19] have made a remarkable improvement comparing to the conventional methods based on the handcrafted features LBP, Gabor-LBP, HOG, SIFT [1, 8, 2, 28]. The situation is same as facial expression recognition based on deep CNNs [14, 40, 22]. Even so, the studies on the face recognition with the facial expression images are limited. [15, 41, 3] propose the 3D based methods to deal with this issue. Kakadiaris et al. [15] present a fully automated framework for 3D face recognition using the Annotated Face Model to converted the raw image of face to a geometric model and a normal map. Then the face recognition is based on the processed image by using the Pyramid and Haar. Zhu et al. [41] presents the method by using the 3D facial model to normalise the facial expression and then maps the normalised face to the 2D image to employ face recognition. Chang et al. [3] describe a method using three different overlapping regions around the nose to employ the face recognition since this region is invariant in the presence of facial expression.

与传统基于手工特征（LBP、Gabor-LBP、HOG、SIFT [1, 8, 2, 28]）的方法相比，SphereFace [19] 取得了显著改进。这一情况与基于深度CNN的面部表情识别研究 [14, 40, 22] 类似。即便如此，针对带有表情的人脸识别研究仍然有限。[15, 41, 3] 提出了基于3D的方法来解决该问题。Kakadiaris等人 [15] 提出了一种全自动3D人脸识别框架，使用标注人脸模型（Annotated Face Model）将原始人脸图像转换为几何模型和法线贴图，随后基于金字塔和Haar特征对处理后的图像进行识别。Zhu等人 [41] 提出通过3D面部模型规范化表情，再将规范化人脸映射至2D图像进行识别的方法。Chang等人 [3] 则描述了一种利用鼻周三个不同重叠区域进行识别的方法，因为该区域在表情变化时保持稳定 [3]。

3. Architecture

3. 架构

The proposed multi-task learning with dynamic weights is based on the deep CNNs (see Figure 1). The hard parameter sharing structure is adopted as our framework, in which the sharing hidden layers are shared between all tasks [26]. The task-specific layers consisting of two branches are respectively dedicated to face verification and facial expression recognition. The two branches have almost identical structures facilitate the transfer learning of facial expression recognition from the pretrained face recognition task. Specifically, the BRANCH 1 can extract the embedded features of bottleneck layer for face verification and the BRANCH 2 uses the fully connected softmax layer to calculate the probabilities of the facial expressions. The deep CNNs in this work are based on the Inception-ResNet structure which have 13 million parameters of about 20 hidden layers in terms of the depth and 3 branches to the maximum in terms of the large. By the virtue of the Inception structure, the size of the parameters is much fewer than other popular deep CNNs such as VGGFace with 138 million parameters.

提出的动态权重多任务学习基于深度卷积神经网络 (CNN) (见图 1)。我们采用硬参数共享结构作为框架，其中所有任务共享隐藏层 [26]。由两个分支组成的任务特定层分别专用于人脸验证和面部表情识别。这两个分支具有几乎相同的结构，便于从预训练的人脸识别任务中迁移学习面部表情识别。具体而言，分支 1 可提取瓶颈层的嵌入特征用于人脸验证，分支 2 使用全连接 softmax 层计算面部表情的概率。本文采用的深度 CNN 基于 Inception-ResNet 结构，具有 1300 万参数，深度约 20 个隐藏层，最大宽度为 3 个分支。得益于 Inception 结构，其参数量远少于其他主流深度 CNN (如 1.38 亿参数的 VGGFace)。

Dynamic-weight-unit The dynamic weights of tasks are generated by the softmax layer connecting to the end of the sharing hidden layers, which can be so called the Dynamicweight-unit. Each element in the Dynamic-weight-unit is corresponding to a weight of a task, thus the size of the Dynamic-weight-unit is equal to the number of weights of tasks, e.g. the size is 2 in this work. Since the weights are generated by the softmax layer, $w1+w2=1$ which can well indicate the relative importance of the tasks. The parameters of this softmax layer are updated by the independent loss function $\mathcal{L}_{3}$ during the training of the networks, which can automatically adjust the weights of tasks in light of the variation of the loss of tasks and drive the networks to always train the hard task firstly by assigning a larger weight.

动态权重单元
任务的动态权重由连接共享隐藏层末端的softmax层生成，因此可称为动态权重单元。动态权重单元中的每个元素对应一个任务的权重，故其尺寸等于任务权重数量（例如本研究中尺寸为2）。由于权重通过softmax层生成，$w1+w2=1$ 能有效反映任务的相对重要性。该softmax层的参数在网络训练期间通过独立损失函数 $\mathcal{L}_{3}$ 更新，可根据任务损失变化自动调整权重，并通过分配更大权重驱使网络始终优先训练困难任务。

4. Multi-task learning with dynamic weights

4. 动态权重的多任务学习

The total loss of the proposed multi-task CNNs is the sum of the weighted losses of the multiple tasks.

所提出的多任务CNN的总损失是多个任务的加权损失之和。

(I) Multi-task loss $\mathcal{L}$ : The multi-task total loss $\mathcal{L}$ is defined as follows:

(I) 多任务损失 $\mathcal{L}$ : 多任务总损失 $\mathcal{L}$ 定义如下:

$$
\mathcal{L}(\mathbf{X};\boldsymbol{\Theta};\Psi)=\sum_{i=1}^{T}w_{i}(\Psi)\mathcal{L}{i}(\mathbf{X}{i};\boldsymbol{\Theta}_{i})
$$

$$
\mathcal{L}(\mathbf{X};\boldsymbol{\Theta};\Psi)=\sum_{i=1}^{T}w_{i}(\Psi)\mathcal{L}{i}(\mathbf{X}{i};\boldsymbol{\Theta}_{i})
$$

where $T$ is the number of the tasks, here $T=2$ . $X_{i}$ and $\Theta_{i}$ are the feature and the parameters corresponding to each task, $\boldsymbol{\Theta}={\Theta_{i}}{i=1}^{T}$ are the overall parameters of the networks to be optimized by $\mathcal{L}$ . $\Psi$ are the parameters of the softmax layer in the Dynamic-weight-unit used to generate the dynamic weights $w_{i}\in[0,1]$ s.t. $\sum w_{i}~=~1$ . Thus ${\mathbf{X}{i},\boldsymbol{\Theta}{i}}\in\mathbb{R}^{d_{i}}$ , where $d_{i}$ is the dime nsion of the features $X_{i}$ , and ${\mathcal{L}{i},w_{i}}\in\mathbb{R}^{1}$ . Particularly, when $w_{1}=1$ , $w_{2}=0$ the multi-task networks are degraded as the single-task networks for face verification (i.e. Branch 1 and sharing hidden layers) while $w_{1}=0$ , $w_{2}=1$ is corresponding to the singletask networks for facial expression recognition (i.e. Branch 2 and sharing hidden layers).

其中 $T$ 是任务数量，此处 $T=2$。$X_{i}$ 和 $\Theta_{i}$ 分别表示各任务对应的特征与参数，$\boldsymbol{\Theta}={\Theta_{i}}{i=1}^{T}$ 是通过 $\mathcal{L}$ 优化的网络总体参数。$\Psi$ 是动态权重单元中 softmax 层的参数，用于生成满足 $\sum w_{i}~=~1$ 的动态权重 $w_{i}\in[0,1]$。因此 ${\mathbf{X}{i},\boldsymbol{\Theta}{i}}\in\mathbb{R}^{d_{i}}$，其中 $d_{i}$ 是特征 $X_{i}$ 的维度，而 ${\mathcal{L}{i},w_{i}}\in\mathbb{R}^{1}$。特别地，当 $w_{1}=1$、$w_{2}=0$ 时，多任务网络退化为面向人脸验证的单任务网络（即分支1及共享隐藏层）；当 $w_{1}=0$、$w_{2}=1$ 时则对应面向面部表情识别的单任务网络（即分支2及共享隐藏层）。

(II) Face verification task loss $\mathcal{L}{1}$ : The loss for face verification task is measured by the center loss [33] joint with the cross-entropy loss of softmax of Branch 1. The loss function of face verification task $\mathcal{L}_{1}$ is given by:

(II) 人脸验证任务损失 $\mathcal{L}_{1}$ : 该任务损失由中心损失 [33] 与分支1的softmax交叉熵损失联合构成，其表达式为:

$$
\mathcal{L}{1}(\mathbf{X}{1};\boldsymbol{\Theta}{1})=\mathcal{L}{s1}(\mathbf{X}{1};\boldsymbol{\Theta}{1})+\alpha\mathcal{L}{c}(\mathbf{X}{1};\boldsymbol{\Theta}_{1})
$$

$$
\mathcal{L}{1}(\mathbf{X}{1};\boldsymbol{\Theta}{1})=\mathcal{L}{s1}(\mathbf{X}{1};\boldsymbol{\Theta}{1})+\alpha\mathcal{L}{c}(\mathbf{X}{1};\boldsymbol{\Theta}_{1})
$$

where $\mathcal{L}{s1}$ is the cross-entropy loss of softmax of Branch 1, $\mathcal{L}{c}$ is the center loss weighted by the hyper parameter $\alpha$ . The $\mathcal{L}{c}$ can be treated as a regular iz ation item of softmax loss $\mathcal{L}_{s1}$ which is given by:

其中 $\mathcal{L}{s1}$ 是分支1的softmax交叉熵损失，$\mathcal{L}{c}$ 是由超参数 $\alpha$ 加权的中心损失。$\mathcal{L}{c}$ 可视为softmax损失 $\mathcal{L}_{s1}$ 的正则化项，其表达式为：

$$
\begin{array}{c}{{\displaystyle\mathcal{L}{s1}(\mathbf{X}{1};\boldsymbol{\Theta}{1})=\sum_{k=1}^{K}-y_{k}l o g P(y_{k}=1|\mathbf{X}{1},\boldsymbol{\theta}{k})}}\ {{\displaystyle=-\sum_{k=1}^{K}y_{k}l o g\frac{e^{f^{\theta_{k}}(\mathbf{X}{1})}}{\sum_{k^{\prime}}^{K}e^{f^{\theta_{k^{\prime}}}(\mathbf{X}_{1})}}}}\end{array}
$$

$$
\begin{array}{c}{{\displaystyle\mathcal{L}{s1}(\mathbf{X}{1};\boldsymbol{\Theta}{1})=\sum_{k=1}^{K}-y_{k}l o g P(y_{k}=1|\mathbf{X}{1},\boldsymbol{\theta}{k})}}\ {{\displaystyle=-\sum_{k=1}^{K}y_{k}l o g\frac{e^{f^{\theta_{k}}(\mathbf{X}{1})}}{\sum_{k^{\prime}}^{K}e^{f^{\theta_{k^{\prime}}}(\mathbf{X}_{1})}}}}\end{array}
$$

where $K$ is the number of the classes, i.e. the number of identities in the training dataset, $y_{k}\in{0,1}$ is the one-shot label of the feature $\mathbf{X}{1}$ , $P(y_{k}|\mathbf{X}{1},\theta_{k})$ is softmax function over the activation function $f^{\theta_{k}}(\mathbf{X}{1})$ where ${\theta_{k}}{k=1}^{K}=\Theta_{1}$ , $\theta_{k}\in\mathbb{R}^{d_{1}}$ . The bottleneck layer of BRANCH 1 is extracted as the feature $\mathbf{X}{1}$ of the input image. The center loss $\mathcal{L}_{c}$ is given by:

其中 $K$ 为类别数（即训练数据集中身份数量），$y_{k}\in{0,1}$ 是特征 $\mathbf{X}{1}$ 的单样本标签，$P(y_{k}|\mathbf{X}{1},\theta_{k})$ 是基于激活函数 $f^{\theta_{k}}(\mathbf{X}{1})$ 的softmax函数（其中 ${\theta_{k}}{k=1}^{K}=\Theta_{1}$，$\theta_{k}\in\mathbb{R}^{d_{1}}$）。将BRANCH 1的瓶颈层提取为输入图像的特征 $\mathbf{X}{1}$。中心损失 $\mathcal{L}_{c}$ 定义为：

$$
\mathcal{L}{c}(\mathbf{X}{1};\boldsymbol{\Theta}{1})=||\mathbf{X}{1}-C_{y_{k}}||
$$

$$
\mathcal{L}{c}(\mathbf{X}{1};\boldsymbol{\Theta}{1})=||\mathbf{X}{1}-C_{y_{k}}||
$$

Where the $C_{y_{k}}$ is the center of the class which $\mathbf{X}{1}$ belonging to, $C_{y_{k}}\in\mathbb{R}^{d_{1}}$ .

其中 $C_{y_{k}}$ 是 $\mathbf{X}{1}$ 所属类别的中心点， $C_{y_{k}}\in\mathbb{R}^{d_{1}}$ 。

(III) Facial expression recognition task loss $\mathcal{L}{2}(\mathbf{X}{2};\Theta_{2})$ : The loss function of facial expression recognition task $\mathcal{L}{2}$ is the cross-entropy loss of the softmax layer of BRANCH 2. The equation of $\mathcal{L}{2}$ is as same as Equation 3 except the $K$ in $\mathcal{L}{2}$ is the number of the categories of the facial expressions, $\mathbf{X}_{2}$ is the bottleneck layer of BRANCH 2, $\Theta2$ is corresponding parameters of this task.

(III) 面部表情识别任务损失 $\mathcal{L}{2}(\mathbf{X}{2};\Theta_{2})$ : 面部表情识别任务的损失函数 $\mathcal{L}{2}$ 是 BRANCH 2 的 softmax 层的交叉熵损失。 $\mathcal{L}{2}$ 的公式与公式 3 相同，只是 $\mathcal{L}{2}$ 中的 $K$ 是面部表情的类别数量， $\mathbf{X}_{2}$ 是 BRANCH 2 的瓶颈层， $\Theta2$ 是该任务对应的参数。

(IV) Generation of the dynamic weights $w_{i}(\Psi)$ : The dynamic weights $w_{i}$ are generated by the softmax layer of the dynamic-weight-unit which is given by:

(IV) 动态权重 $w_{i}(\Psi)$ 的生成：动态权重 $w_{i}$ 由动态权重单元的 softmax 层生成，其表达式为：

$$
w_{i}(\mathbf{Z};\Psi)=\frac{e^{f^{\psi_{i}}(\mathbf{Z})}}{\sum_{i^{\prime}}^{T}e^{f^{\psi_{i^{\prime}}}(\mathbf{Z})}}
$$

$$
w_{i}(\mathbf{Z};\Psi)=\frac{e^{f^{\psi_{i}}(\mathbf{Z})}}{\sum_{i^{\prime}}^{T}e^{f^{\psi_{i^{\prime}}}(\mathbf{Z})}}
$$

where the $\mathbf{Z}\in\mathbb{R}^{d_{z}}$ is the flat output of the last layer of the sharing hidden layers. $T$ is the number of the tasks, here $T{=}2$ . $\psi_{i}$ is parameters in the softmax layer of the dynamic- weight-unit ${\psi_{i}}{i=1}^{T}=\Psi,\psi_{i}\in\mathbb{R}^{d_{z}}.\dot{f}^{\psi_{i}}(\mathbf{Z})$ is activation function which is given by:

其中 $\mathbf{Z}\in\mathbb{R}^{d_{z}}$ 是共享隐藏层最后一层的平坦输出。$T$ 是任务数量，此处 $T{=}2$。$\psi_{i}$ 是动态权重单元 (dynamic-weight-unit) 中 softmax 层的参数 ${\psi_{i}}{i=1}^{T}=\Psi,\psi_{i}\in\mathbb{R}^{d_{z}}$。$\dot{f}^{\psi_{i}}(\mathbf{Z})$ 是由下式给出的激活函数：

$$
f^{\psi_{i}}({\bf Z})=\psi_{i}{\bf Z}^{T}+b_{i}
$$

$$
f^{\psi_{i}}({\bf Z})=\psi_{i}{\bf Z}^{T}+b_{i}
$$

Note that, we do not use the Relu function as the activation function since Relu discards the values minors zero. This shrinks the range of the variation of the dynamic weights $w_{i}$ .

需要注意的是，我们不使用Relu函数作为激活函数，因为Relu会丢弃小于零的值。这会缩小动态权重$w_{i}$的变化范围。

(V) Update of the dynamic weights $w_{i}$ : Rather than using the total loss to update the dynamic weights, we propose a new loss function to update the dynamic weights which can drive the networks always train the hard task. The proposed new loss function for updating the dynamic weights is given by:

(V) 动态权重 $w_{i}$ 的更新：不同于使用总损失来更新动态权重，我们提出了一种新的损失函数来更新动态权重，该函数能驱使网络始终训练困难任务。所提出的用于更新动态权重的新损失函数如下：

$$
\mathcal{L}{3}(\mathbf{Z};\Psi)=\sum_{i=1}^{T}\frac{w_{i}(\psi_{i})}{\mathcal{L}{i}(\Theta_{i})}\quad s.t.\quad\sum w_{i}=1
$$

$$
\mathcal{L}{3}(\mathbf{Z};\Psi)=\sum_{i=1}^{T}\frac{w_{i}(\psi_{i})}{\mathcal{L}{i}(\Theta_{i})}\quad s.t.\quad\sum w_{i}=1
$$

Note that, $\mathcal{L}{i}{\boldsymbol{\Theta}{i}}$ is independent with $w_{i}(\psi_{i})$ since $\Theta_{i}\cap$ ${\psi_{i}=\emptyset}$ , $i\in[1,..,T]$ , thus $\mathcal{L}{i}$ is constant for the dynamic weight update loss function $\mathcal{L}_{3}$ .

注意到，$\mathcal{L}{i}{\boldsymbol{\Theta}{i}}$ 与 $w_{i}(\psi_{i})$ 无关，因为 $\Theta_{i}\cap$ ${\psi_{i}=\emptyset}$，$i\in[1,..,T]$，因此 $\mathcal{L}{i}$ 对于动态权重更新损失函数 $\mathcal{L}_{3}$ 是常数。

(VI) Qualitative analysis shows that when the loss of the task $\mathcal{L}{i}$ is small, i.e. the reciprocal of the $\mathcal{L}{i}$ is large, thus loss $\mathcal{L}{3}$ will try to reduce the loss by decreasing the value of $w_{i}$ . That is to say, when the task is easy with a small loss the weight of the task will be assigned by a small value. On the contrary, the hard task with a large loss will be assigned by a large weight, which enable the networks always focus on training the hard task firstly. The update of the dynamic weights $w_{i}$ is essentially the update of the parameters $\psi_{i}$ which generate the dynamic weights.

(VI) 定性分析表明，当任务损失$\mathcal{L}{i}$较小时，即$\mathcal{L}{i}$的倒数较大时，损失$\mathcal{L}{3}$会通过减小$w_{i}$的值来降低损失。也就是说，当任务简单且损失较小时，该任务的权重会被赋予较小的值。相反，损失较大的困难任务会被赋予较大的权重，这使得网络始终优先训练困难任务。动态权重$w_{i}$的更新本质上是生成动态权重的参数$\psi_{i}$的更新。

(VII) Quantitative analysis: Considering the Equation 5 and Equation 6, the gradient of the $\psi_{i}$ can be given

(VII) 定量分析：根据公式5和公式6，$\psi_{i}$的梯度可表示为

by

作者：

$$
\nabla\psi_{i}=\frac{\partial\mathcal{L}{3}}{\partial\psi_{i}}=\frac{1}{\mathcal{L}{i}}\frac